注重变式训练，培养创新思维

福建省莆田市第二十五中学 蔡 昆

当前倡导的课程改革，其核心就是培养学生的创新能力，课堂教学正是实施课程改革的主渠道，因此，提高课堂教学效率，培养学生创新思维已成为共识。高中数学教学中若能根据教材特点，结合学生实际，选择变式教学，注重变式训练，有助于激发学生学习的积极性和主动性，减轻课业负担，提高教学质量，培养出思维发散的创造型人才。

由易到难，由浅入深，由简到繁，这是学习的规律。在应用均值不等式求“积定”一类最值问题的教学中，我精心设计16道不同层次的变式训练例题，有效突破了教学难点，课堂气氛格外活跃，教学效果优良。

[分析]：在引导学生总结均值不等式的条件：“一正、二定、三相等”后，让学生运用均值不等式，加深对均值不等式的理解。

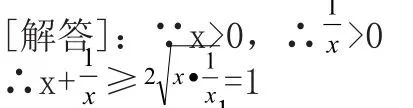
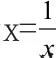
故y的最小值为2.

[分析]：此处x与的积虽为定值，但x与均为负值，不符合均值不等式条件，学生思维暂时受阻。如何实现由负值向正值的转变，是解决问题的关键，启发学生联系不等式的性质可获思路。

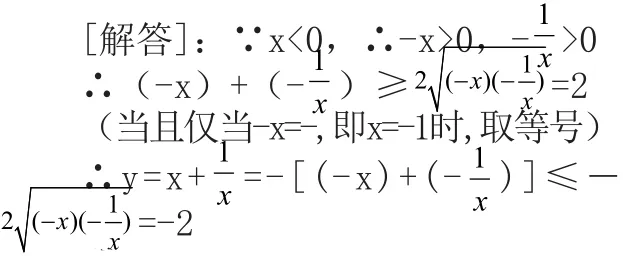
即y最大值为-2.

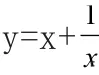
[分析]：本题主要考查学生的讨论分析能力，由前面求解可知要分x＞0与x＜0讨论，即：

若x＞0，则y有最小值2.

若x＜0，则y有最大值－2.

[解答]：略

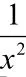
[备注]：这里为什么要将x拆成相等的两项的和，而不拆成其它形式，可通过实际变化来分析，让学生体会到其中的奥妙。

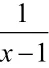
∴y最小值为3.

[备注]：从不同角度进行变式，步步深入，诱发思维。

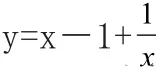
[分x析 ]：由于x＞0，x与的积为定值，故移项后，

（当且仅当x=1时,取等号）

[解答]：略

[分析]：要直接添、拆项有点困难，可进行凑项。

[解答]：略

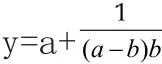
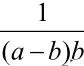
∴y的最小值为3.

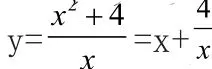
[解答]：略

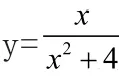
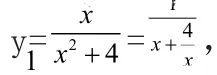
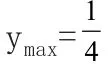
[解答]：略

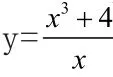
易求得（当且仅当时，取等号）

[解答]：略

[分析]：由变式题12与变式题13，可知

（当且仅当时，取等号）

[解答]：略

[分析]：虽含有根号，但由于x2+2=x2+1+1

（当且仅当x=0时取等号）

∴y的最小值为2.

[解答]：略

一个看似简单而重要的公式，通过精心设计的变式例题训练，引导学生共同探索、辨析，降低了综合性难题的梯度，突破了教学难点，使学生所学知识与方法融会贯通。因此高中数学教学中，若能根据学生认知规律，遵循循序渐进的教学原则，设计一组能易中求活、求深、求精的变式训练题，不仅能广开学生思路，拓展学生思维，且对培养学生思维的灵活性和创新能力是大有裨益的。