用二分法求方程的近似解 教学设计
中国人民大学附属中学朝阳学校 刘富蕊
一、教材分析
本节内容位于数学必修1第三章第一节“函数与方程”,共分2个课时。第一课时学习了“方程的根与函数零点的关系”,本节是第二课时,二分法是求方程近似解的常用方法,它体现了函数的思想以及函数与方程的联系,为高中数学中函数与方程思想、数形结合思想、二分法的算法思想打下了基础,为必修三中算法内容的学习做了铺垫。二分法体现了数学的逼近思想,对学生以后学习微积分的知识起了奠基的作用,因此决定了它的重要地位。
二、学情分析
本班是普通班,学生的计算能力、数形结合能力、用数学符号语言表达能力较为薄弱。学生通过前面的学习,对方程的根的存在性以及函数零点和方程的根的关系有了一定的认识。学生掌握了初中所学函数的图像和性质,并具有了一定的数形结合的思想,这为理解函数零点附近的函数值符号提供了直观认识,在此基础上介绍用二分法求函数零点近似值,也就水到渠成。
三、教学目标
1.会用二分法求方程的近似解,在求解过程中体会用二分法求方程近似解的步骤与原理;
2. 通过对二分法原理的探索,引导学生用联系的观点理解函数与方程,形成用函数的观点处理问题的意识,通过求具体方程近似解介绍二分法并总结其步骤,体现了从具体到一般的认知过程,同时渗透算法思想;
3.在解决问题的过程中,培养学生克服困难的勇气、增强解决问题的信心,感受成功的喜悦。
四、教学重难点
重点:用二分法求方程的近似解
难点:精确度的概念和二分法的逼近思想
五、教学过程

教学环节 师生活动设计意图复习引入 上节课我们学习了方程的根与函数零点的关系:方程f x=() 0有根⇔函数 有零点判断在某区间上函数零点存在的方法:零点存在性定理问题1:已知方程yf x=()的图像与x轴有交点⇔函数yf x=(),你能解这个方程吗?预设:1.学生用求根公式求解,发现不行2.学生因式分解求解,也行不通追问:这个方程有根吗?你猜有几个根?预设:1.转化为两个函数,求交点,作图观察2.描点作图,画函数2 3 3 0 xx+-=3复习回顾,为今天所学作知识铺垫。抛出问题,通过图像直观感知零点的初始存在区间yxx=+-2 3 3 3的大致图像探究新知 问题2:如果有根,根存在的大致范围是多少?预设:学生根据图像猜测根存在区间(0,1)师:在实际生活或工业中,往往只需要求出近似解就可以,如果对解的精确程度要求不高,这个区间里的值都可以看成函数零点的近似值。追问:如果想要更精确一些,怎么办?预设:缩小区间问题3:如何缩小区间?讨论一下预设:1.学生在(0,1)内随机取不同的值,求出函数值,看符号,并利用零点存在性定理不断缩小区间。2.学生选取区间中点,求函数值,判断符号,方法简单、速度快。3.学生取区间三等分点或四等分点或十等分点一点点逼近函数零点。教师在黑板上演示二分法缩小区间,区间端点不断逼近零点的过程。教师引导学生数形结合,找到方法不断缩小区间,并比较大家采取的方法,肯定大家的做法都可以。不同的函数采用不同的方法快慢不同,与零点在区间的位置有关。对于所有函数来讲,二分法还是比较快的,二分法的优势:有规律、简单、速度快,从而一般采用二分法来解决函数的零点问题。二分法定义:对于区间学生认为求方程的根应该是求一个精确值,在这里,为学生找根存在的区间作铺垫。让学生体会不同缩小区间的方法,让区间端点不断逼近零点的过程引出二分法的定义[ ]a b ,上连续不断且fafb<()() 0的函数yf x=()辨析二分法的概念,让学生更加清楚地明白二分法的适用范围,通过不断地把函数 的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.判断:是否可以用二分法求下列函数的零点?f x()让学生明白近似解是针对不同的精确度而言的。问题4:区间要一直缩小下去吗?预设:1.找到使得函数值为0的x停止2.找不到使得函数值为0的x,无限进行下去。
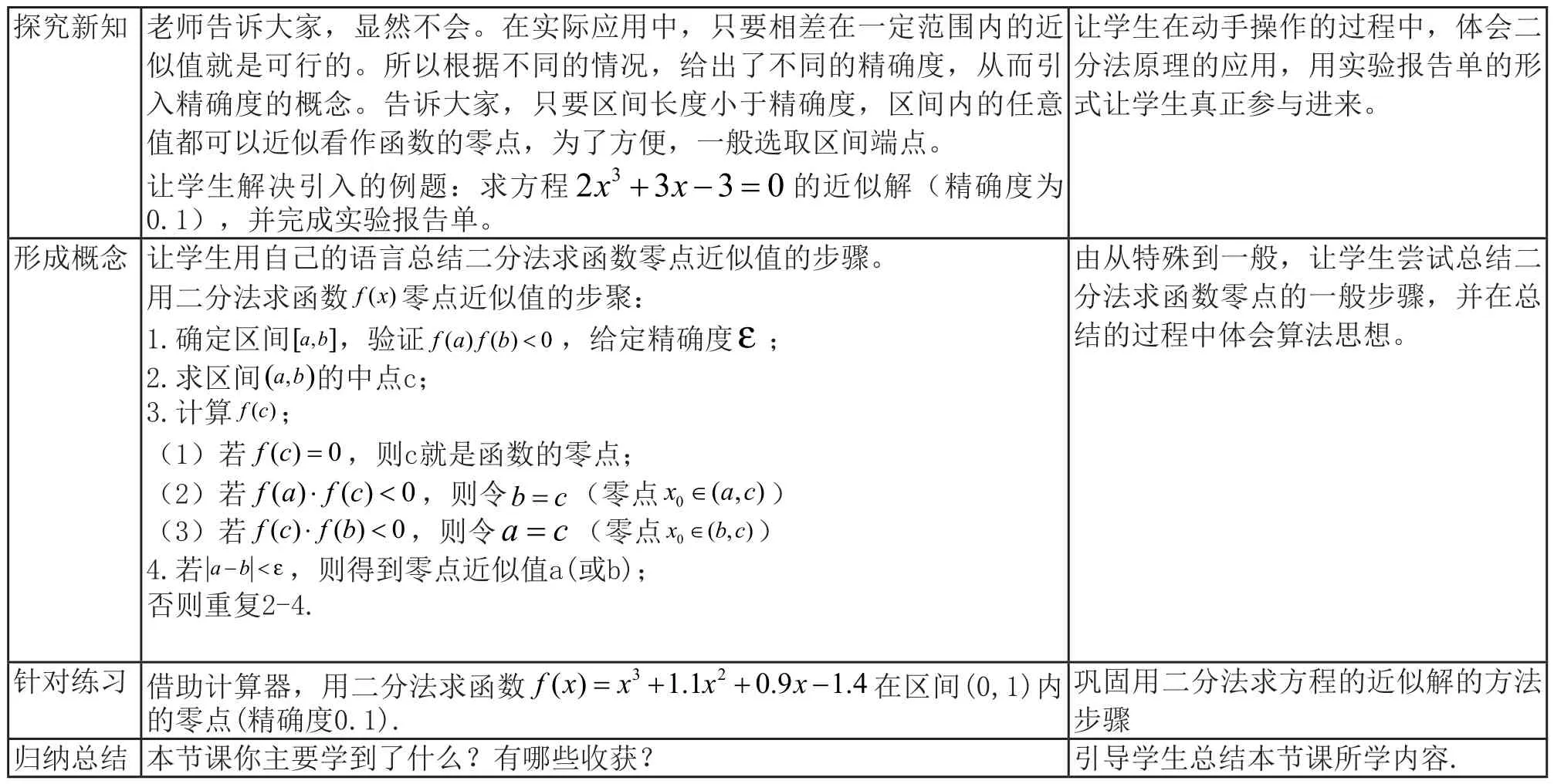
探究新知 老师告诉大家,显然不会。在实际应用中,只要相差在一定范围内的近似值就是可行的。所以根据不同的情况,给出了不同的精确度,从而引入精确度的概念。告诉大家,只要区间长度小于精确度,区间内的任意值都可以近似看作函数的零点,为了方便,一般选取区间端点。让学生解决引入的例题:求方程让学生在动手操作的过程中,体会二分法原理的应用,用实验报告单的形式让学生真正参与进来。的近似解(精确度为0.1),并完成实验报告单。2 3 3 0 xx+-=3形成概念 让学生用自己的语言总结二分法求函数零点近似值的步骤。用二分法求函数 零点近似值的步聚:1.确定区间f x();2.求区间[ ]a b,,验证f a f b<()() 0,给定精确度ε由从特殊到一般,让学生尝试总结二分法求函数零点的一般步骤,并在总结的过程中体会算法思想。的中点c;3.计算( ),a b;(1)若()f c,则c就是函数的零点;(2)若f c=() 0 f af c⋅<()() 0,则令bc=(零点xa c∈0(,))(3)若f cf b⋅<()() 0,则令ac=(零点xb c∈0(,))4.若 ,则得到零点近似值a(或b);否则重复2-4.abε-<针对练习 借助计算器,用二分法求函数巩固用二分法求方程的近似解的方法步骤归纳总结 本节课你主要学到了什么?有哪些收获? 引导学生总结本节课所学内容.在区间(0,1)内的零点(精确度0.1).f xxxx() 1.1 0.9 1.4=++-3 2

