数形结合的思想方法

广西宜州市高级中学 陈文安

数形结合的题目出现在高中数学知识的方方面面上，把图象作为工具、载体，以此寻求解题思路或制定解题方案，真正体现数形结合的简捷、灵活特点的多是填空小题。对数形结合等思想方法的考查，是对数学知识在更高层次的抽象和概括能力的考查，是对学生思维品质和数学技能的考查，是新课标高考明确的一个命题方向。

数形结合的基本思路是：根据数的结构特征，构造出与之相应的几何图形，并利用图形的特性和规律，解决数的问题；或将图形信息全部转化成代数信息，使解决形的问题转化为数量关系的讨论。

一、高考试题对数形结合的考查主要涉及的几个方面

集合问题中Venn图（韦恩图）的运用；

数轴及直角坐标系的广泛应用；函数图象的应用；

数学概念及数学表达式几何意义的应用；

解析几何、立体几何中的数形结合。

二、数形结合思想解决的问题常有以下几种

构建函数模型并结合其图象求参数的取值范围；

构建函数模型并结合其图象研究方程根的范围；

构建函数模型并结合其图象研究量与量之间的大小关系；

构建函数模型并结合其几何意义研究函数的最值问题和证明不等式；构建立体几何模型研究代数问题；构建解析几何中的斜率、截距、距离等模型研究最值问题；

构建方程模型，求根的个数；

研究图形的形状、位置关系、性质等。

三、运用数形结合思想分析解决问题时，要遵循三个原则

1.等价性原则

要注意由于图象不能精确刻画数量关系所带来的负面效应；

2.双方性原则

既要进行几何直观分析，又要进行相应的代数抽象探求，仅对代数问题进行几何分析容易出错；

3.简单性原则

不要为了“数形结合”而数形结合，具体运用时，一要考虑是否可行和是否有利；二要选择好突破口，恰当设参、用参、建立关系，做好转化；三要挖掘隐含条件，准确界定参变量的取值范围，特别是运用函数图象时应设法选择动直线与定二次曲线为佳。

四、进行数形结合的信息转换，主要有三个途径

建立坐标系，引入参变数，化静为动，以动求解，如解析几何；

构造成转化为熟悉的函数模型，利用函数图象求解；

构造成转化为熟悉的几何模型，利用图形特征求解。

五、常见的“以形助数”的方法有

借助于数轴、文氏图，树状图，单位圆；

借助于函数图象、区域(如线性规划)、向量本身的几何背景；

借助于方程的曲线，由方程代数式，联想其几何背景，并用几何知识解决问题，如点，直线，斜率，距离，圆及其他曲线，直线和曲线的位置关系等，对解决代数问题都有重要作用，应充分予以重视.以下通过几例略加说明。

类型一、数轴、韦恩图在集合中的应用

【例1】设集合A={x|1＜x＜4}，集合B={x|x2-2x-3≤0}, 则A∩CRB（）=（ ）

A。(1,4) B。(3,4)C。.(1,3) D。(1,2)∪（3,4）

【解析】B={x|x2-2 x-3≤0}=(x|-1≤x≤3)，A∩（CRB）={x|1＜x＜4}∩{x|x＜-1}或x＞3}={x|3＜x＜4}。故选B.

【小结】不等式型集合的交、并集通常可以利用数轴进行，解题时注意验证区间端点是否符合题意。

类型二、利用数形结合思想解决函数问题

【例2】已知若f(x)的最小值记为h(t)，写出的表达式。

【解析】由于

所以抛物线f(x)的对称轴为，开口向上，

①当时，f(x)在[t，t+1]上单调递增（如图①所示），

∴当x=t时，f(x)最小，即

②当，即时，f(x)在上递减，在上递增（如图②）。

∴当时，f(x)最小，即

③当时，f(x)在[t，t+1]上单调递减（如图③）。

∴当x=t+1时，f(x)最小，即

综合①②③得

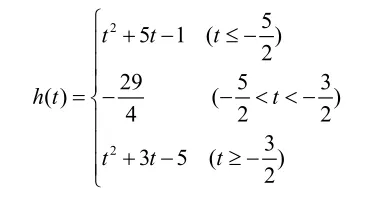
【小结】通过二次函数的图象确定解题思路，直观、清晰，体现了数形结合的优越性。应特别注意，对于二次函数在闭区间上的最值问题，应抓住对称轴与所给区间的相对位置关系进行讨论解决。首先确定其对称轴与区间的位置关系，结合函数图象确定在闭区间上的增减情况，然后再确定在何处取最值。

类型三：利用数形结合思想解决方程中的参数问题

【例3】若关于x的方程有两个不同的实数根，求实数m的取值范围。

【解析】画出和的图象，

当直线即时，两图象有两个交点。

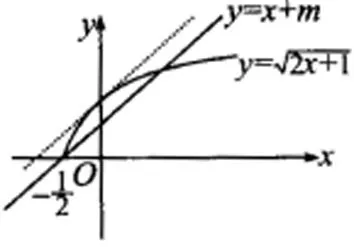
又由当曲线曲线相切时，二者只有一个交点，设切点则即，解得切点(0,1)，

又直线过切点(0,1)，得m=1，

∴当时，两函数图象有两个交点，即方程有两个不等实根。

【小结】作图时，图形的相对位置关系不准确，易造成结果错误。

类型四：依据式子的结构，赋予式子恰当的几何意义，数形结合解答

【例4】求函数的最大值和最小值

【解析】可看作是单位圆上的动点，为圆外一点，如图，

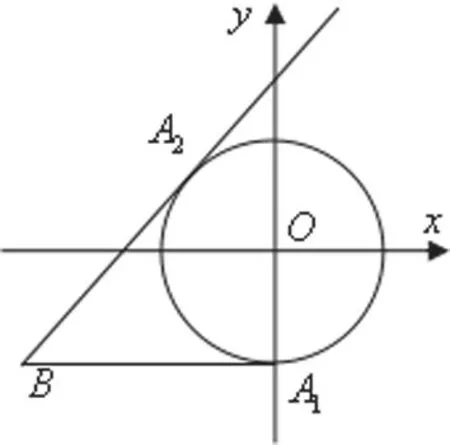
由图可知：显然

设直线的方程：

【小结】一些代数式所表示的几何意义往往是解题的关键，故要熟练掌握一些代数式的几何意义：

（1）表示动点（x，y）与定点（a，b）两点间的距离；

（2）表示动点（x，y）与定点（a，b）两点连线的斜率；

（3）求ax+by的最值，就是求直线ax+by=t在y轴上的截距的最值。

线性规划是借助平面区域表示直线、不等式等代数表达式，最终借助图形的性质解决问题。巧妙运用数形结合的思想方法解决一些抽象的数学问题，可起到事半功倍的效果，数形结合的重点是研究“以形助数”。是通过“以形助数”（将所研究的代数问题转化为研究其对应的几何图形）或“以数助形”（借助数的精确性来阐明形的某种属性），将抽象思维与形象思维有机地结合起来，使抽象问题具体化，复杂问题简单化，在数学解题中具有极为独特的策略指导与调节作用。