计及寄生电容和纹波电流的电压源型逆变器死区效应与补偿方法
谢晔源, 谢 瑞, 李成敏, 周志超, 李武华
(1. 南京南瑞继保电气有限公司, 江苏 南京 211102; 2. 浙江省电力设计院有限公司, 浙江 杭州 310013; 3. 浙江大学电气工程学院, 浙江 杭州 310027)
计及寄生电容和纹波电流的电压源型逆变器死区效应与补偿方法
谢晔源1, 谢 瑞2, 李成敏3, 周志超2, 李武华3
(1. 南京南瑞继保电气有限公司, 江苏 南京 211102; 2. 浙江省电力设计院有限公司, 浙江 杭州 310013; 3. 浙江大学电气工程学院, 浙江 杭州 310027)
电压源型逆变器中固有的死区效应降低了输出电压的品质。为了精确补偿死区效应,需要建立死区效应导致的逆变器输出电压失真的精确模型。但是,已有死区效应模型没有考虑开关管等效并联电容和电感电流纹波对于死区效应的影响,导致死区补偿结果难以优化。本文通过详细分析和推导,发现寄生电容和纹波电流会影响输出电压的精度,并给出了输出电压误差的精确数学表达式。在此基础上,本文提出一种在线、自适应的死区精确补偿方法。最后,通过仿真和实验证明了本文分析的正确性和死区补偿方法的有效性。
电压源型逆变器; 死区效应补偿; 寄生电容; 纹波电流; 电能质量
1 引言
在电压源型逆变器中,为了防止桥臂上下开关管的直通,上下功率器件切换时刻会引入一段死区时间。死区时间会导致目标电压和实际输出电压之间产生误差,引发输出电压侧出现低次谐波[1],从而降低了逆变器的性能。
为了补偿死区效应,国内外学者提出了多种死区补偿方法。最常用的思路为在PWM调制器中引入一个与电压误差等效的补偿量来抵消死区影响[2]。在实际运用中,由于电流纹波等非理想因素的影响,确定电流过零点和死区导致的电压误差是该补偿思路的难点。
文献[3-5]根据死区效应的特点提出了通过反馈来抑制死区效应带来的电压误差的影响。文献[6,7]根据电流过零区域的特征提出了在线补偿方法。目前的大多数补偿方法仅依据死区时间的大小和电感电流的方向来计算电压误差,忽视了开关管等效并联电容和电感电流纹波对死区效应的影响。文献[8-12]的研究表明电压误差会受到寄生电容或电流纹波的影响,尤其是在电流过零附近区域,并提出了对应的补偿策略。然而,文献[3-12]的研究并没有综合考虑开关管的等效并联电容和电感电流纹波对死区效应的影响。
本文建立了计及电感电流和寄生电容的死区效应的综合模型,实现了输出电压误差的精确建模。在此基础上,提出了一种具有动态调整能力的死区效应的补偿新方法。试验结果表明,本文提出的方法对于死区效应具有很好的补偿效果。
2 死区效应的精确模型
2.1 理想条件下死区效应
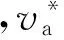

图1 电压源型逆变器单个桥臂电路Fig.1 One phase leg of voltage source inverter

图2 理想条件下输出电压波形Fig.2 Phase voltage waveforms under ideal conditions

(1)
式中,T为开关周期;Td为死区时间;V为母线电压。
2.2 计及寄生电容和纹波电流的死区效应
实际电路中,非理想的开关管存在等效并联寄生电容。由于电容两端的电压不能突变,桥臂输出电压的上升和下降过程无法瞬时完成。图1中,当iL<0时,若下管S2关断,等效并联电容C2通过电感电流iL充电,等效并联电容C1通过电感电流放电。该过程持续时间相对于整个开关周期来说很短,可近似认为充放电电流保持恒定。同样地,当iL>0时,S1关断,C2通过电感电流iL放电。设i1和i2分别为输出电压上升和下降时的电感电流值,桥臂输出电压的自然上升时间t1和下降时间t2为:

(2)
式中,C1=C2=2C。从式(2)可知,若电感电流处于过零点附近区域,i1和i2较小,t1和t2较大。以电压上升过程为例,如果上升时间小于死区时间,桥臂输出电压会自然地上升到母线电压。如果上升时间超过了死区时间,死区时间结束之后上管S1立刻导通,输出电压将会被立刻拉高到母线电压。因此,考虑了等效并联电容的影响后,桥臂输出电压的波形取决于上升或下降时间与死区时间的相对关系。
综合以上分析,电感电流纹波和开关管等效并联电容均会影响桥臂在死区阶段的电压波形,如图3所示。补偿死区带来的误差电压时需综合考虑二者的影响。

图3 考虑并联电容和电流纹波之后的输出电压波形Fig.3 Waveforms of phase voltage considering parasitic capacitance and inductor current
2.3 电压误差建模
图3显示桥臂输出电压的波形随着电感电流的大小和方向的改变而改变。考虑电感电流极性以及桥臂电压的上升和下降过程,一共有8种情况,其输出电压波形如图4所示,分述如下。
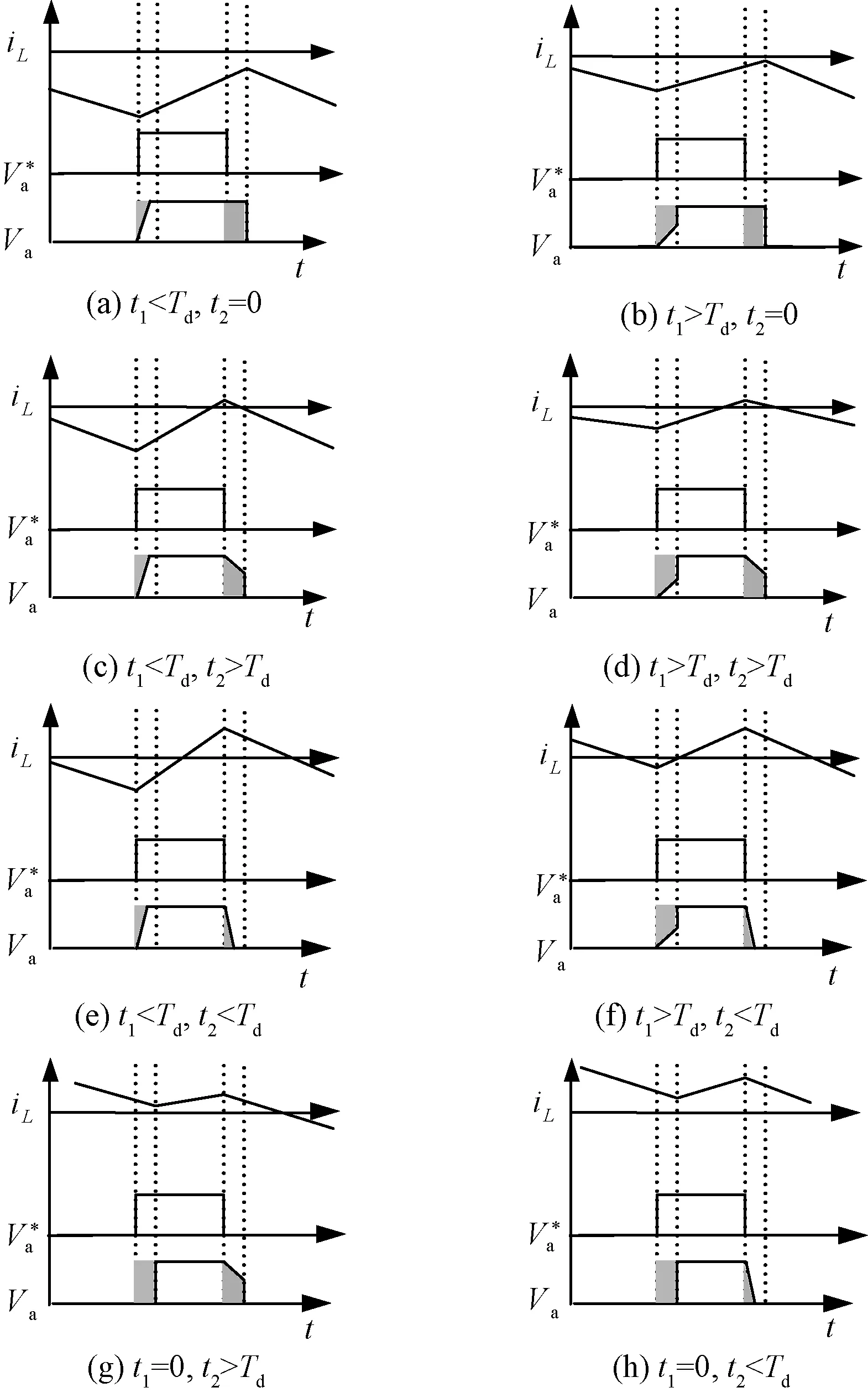
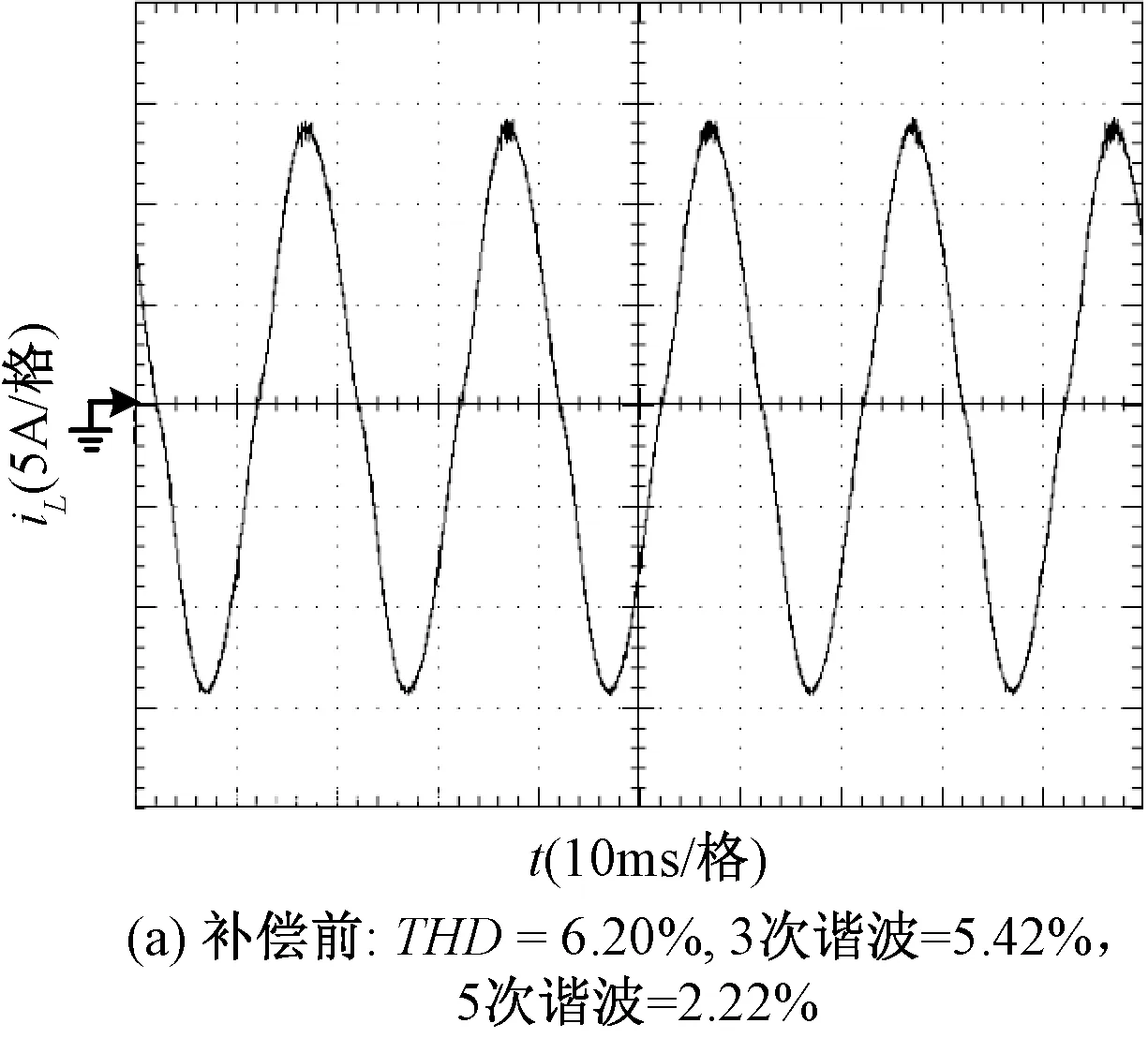
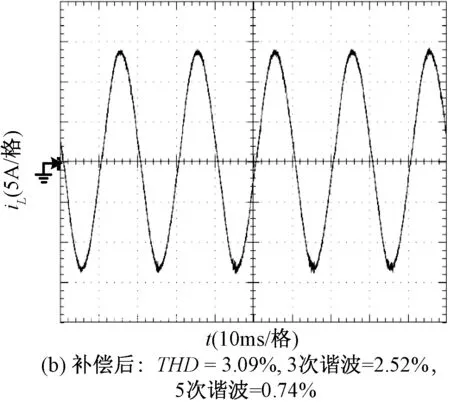
(1)i1 S2关断之后,电感电流向C2充电,输出电压近似线性上升。由于上升时间t1小于死区时间Td,输出电压在上管S1开通之前上升到了母线电压,阴影部分面积表示损失的电压伏秒值。S1关断之后,并联二极管继续导通,输出电压为母线电压,直到下管S2导通。其中阴影部分面积为增加的桥臂输出电压的伏秒值。死区时间带来的单个开关周期内的电压偏差ve可通过阴影部分的面积计算得到: (3) (2)i1 当上管S2关断后,电感电流值很小,C2两端的电压缓慢上升,导致电压自然上升到母线电压的时间超过死区时间。当死区时间结束后,上管S1开通,桥臂输出电压会立刻上升到母线电压。其中梯形阴影部分面积为损失的电压。电压下降的波形与情形(1)类似,此处不再赘述。电压偏差为: (4) 图4 考虑电感电流纹波的输出电压波形Fig.4 Output voltage for different inductor currents (3)i1<0,i2>0,t1 输出电压的上升波形和情形(1)相同。当上管S1关断,电感电流对C2放电,由于电感电流的值很小,电压下降很慢,自然降到0的时间超过了死区时间。死区时间结束之后,下管S1开通,输出电压立刻下降到0。电压误差为: (5) (4)i1<0,i2>0,t1>Td,t2>Td(如图4(d)所示) 该条件下桥臂输出电压的上升时间和下降时间都超过了死区时间,电压误差为: (6) (5)i1<0,i2>0,t1 桥臂输出电压的上升时间和下降时间都小于死区时间,电压误差为: (7) (6)i1<0,i2>0,t1>Td,t2 电压误差为: (8) (7)i1>0,i2>0,t1=0,t2>Td(如图4(g)所示) 当下管S2关断,D2继续导通,va被钳位到0直到S1开通,阴影部分面积为损失的电压。当S1关断之后,电感电流对C2缓慢放电,va的下降时间超过了死区时间,电压误差为: (9) (8)i1>0,i2>0,t1=0,t2 电压上升波形和情形(7)类似。桥臂输出电压va在下管S2开通之前自然下降到0,电压误差为: (10) 目前最有效的死区补偿方法的基本原理为在PWM调制器中添加一个补偿信号从而抵消电压误差。该种补偿方法简洁直观,能够较好地减小死区效应带来的电压误差,且独立于控制环的设计,因此得到了广泛的应用。 根据伏秒平衡原理,电压误差可以通过调节相应的占空比来实现,补偿的占空比dComp为: (11) 本文采用类似的补偿思路,但是补偿信号的产生是基于第2节推导的精确数学模型,因此可以实现高精度的补偿。基于式(11),不同条件下的补偿占空比如表1所示。 (12) 式中,Δi为电感电流的纹波峰峰值,以单极性SPWM调制为例,可以通过式(13)计算得到: (13) 式中,d为当前开关周期的占空比;vL为电感两端的电压;L为电感值。 表1 不同条件下的补偿占空比Tab.1 Compenated duty cycle in different cases 表1显示补偿的占空比是电感电流平均值和电感电流纹波的函数,图5给出了补偿占空比随着电感电流平均值和电感电流纹波变化的一个算例结果。 图5 算例分析Fig.5 Computed example 由已有的研究可知,现有死区补偿方法存在电流过零点检测难题[3],原因在于认为补偿占空比只与电流的平均值有关,即 (14) 而本文提出的补偿占空比为电感电流平均值和电流纹波的函数,即 (15) 由于考虑了电流纹波的影响,本文提出的补偿方法可以看成是电流纹波和平均电流的二元函数,比现有补偿方法多了一个维度。由于补偿占空比的计算模型中包含了电感电流纹波,因此不存在电流过零点检测问题。 为了进一步验证提出补偿策略的有效性,本文搭建了一台5kV·A的并网逆变器并进行了相关实验,并网逆变器的主要参数如表2所示。 表2 并网逆变器的主要参数Tab.2 Main parameters of inverter 4.1 桥臂输出电压波形 图6显示了桥臂输出电压在电流过零区域的上升沿和下降沿,iL指开关管开通或者关断时刻电感电流瞬时值。图6(a)中,若桥臂输出电流小于0,当死区时间结束,下管开通,桥臂输出电压立刻被拉到0,如波形(1)所示。若桥臂输出电流大于0,上管关断,开关管的等效并联电容储存的电荷由电感电流抽走,当电流绝对值较大时,电压自然下降到0时间小于死区时间,电压波形如波形(2)所示。当电流绝对值较低,电压下降时间超过了死区时间,电压波形如波形(3)所示。桥臂电压上升时的情况与此类似,如图6(b)所示。输出电压波形与理论分析一致。 图6 桥臂输出电压试验波形Fig.6 Waveforms of output voltage 4.2 补偿结果波形 图7为控制器内部实时计算的补偿占空比与采样回来的电感电流平均值波形图。 图7 dComp与电感电流平均值关系Fig.7 Relationship between dComp and average current 图8为补偿前后并网电流的波形对比。没有死 区补偿时,电流THD为6.20%,采用提出的补偿方法之后,电流THD降为3.09%。另外,死区效应带来的谐波主要为低次谐波[1],对应的3次、5次谐波在补偿之后都得到了有效的抑制。实验结果表明,本文提出的死区补偿方法能够有效补偿死区效应。 图8 补偿前后并网电流波形对比Fig.8 Output current with and without compensation 本文详细分析了计及寄生电容和纹波电流的电压源型逆变器死区效应,推导了死区补偿占空比的表达式。相对于传统死区效应模型,本文所提的模型更接近于实际物理模型。在此基础上,提出了具有自适应在线补偿能力的死区补偿方法,实现了高品质的电压输出。实验结果验证了本文分析的正确性和补偿方法的有效性。 [1] Dodson R C, Evans P D, Yazdi H T, et al. Compensating for dead time degradation of PWM inverter waveforms [J]. IEE Proceedings B-Electric Power Applications, 1990, 137(2): 73-81. [2] Leggate D, Kerkman R J. Pulse based dead time compensator for PWM voltage inverters [A]. Proceedings of the 1995 IEEE IECON 21st International Conference on Industrial Electronics, Control, and Instrumentation [C]. 1995. 1: 474-481. [3] 宋文祥, 张旭 (Song Wenxiang,Zhang Xu).基于电流矢量的三电平逆变器死区和管压降补偿策略 (Dead time and forward voltage compensation strategy of three level inverter based on the current vector)[J]. 电工电能新技术 (Advanced Technology of Electrical engineering and Energy),2012,31(2):47-51. [4] Kim H S, Moon H T, Youn M J. On-line dead-time compensation method using disturbance observer [J]. IEEE Transactions on Power Electronics, 2003, 18(6): 1336-1345. [5] 史丽萍, 李佳佳, 马艳红, 等(Shi Liping, Li Jiajia, Ma Yanhong, et al.). 基于电压空间矢量的STATCOM直接电流控制新方法(New direct current control method for STATCOM based on voltage space vector) [J]. 电工电能新技术(Advanced Technology of Electrical engineering and Energy), 2015, 34(12):19-24. [6] 杨波, 吴建德, 李武华, 等 (Yang Bo, Wu Jiande, Li Wuhua, et al.). 在线自适应 PWM 死区消除方法 (Online adaptive dead-time elimination method for PWM voltage source inverters) [J]. 电工技术学报(Transactions of China Electrotechnical Society), 2011, 26(11): 45-52. [7] 周华伟, 温旭辉, 赵峰, 等 (Zhou Huawei, Wen Xuhui, Zhao Feng, et al.). 一种新颖的电压源逆变器自适应死区补偿策略(A novel adaptive dead-time compensation strategy for VSI) [J]. 中国电机工程学报(Proceedings of the CSEE), 2011, 31(24): 26-32. [8] Oliveira A C, Jacobina C B, Lima A M N. Improved dead-time compensation for sinusoidal PWM inverters operating at high switching frequencies [J]. IEEE Transactions on Industrial Electronics, 2007, 54(4): 2295-2304. [9] Zhang Z, Xu L. Dead-time compensation of inverters considering snubber and parasitic capacitance [J]. IEEE Transactions on Power Electronics, 2014, 29(6): 3179-3187. [8] Mannen T, Fujita H. Dead-time compensation method based on current ripple estimation [J]. IEEE Transactions on Power Electronics, 2015, 30(7): 4016-4024. [10] Herrán M A, Fischer J R, González S A, et al. Adaptive dead-time compensation for grid-connected PWM inverters of single-stage PV systems [J]. IEEE Transactions on Power Electronics, 2013, 28(6): 2816-2825. [11] Kerkman R J, Leggate D, Schlegel D W, et al. Effects of parasitics on the control of voltage source inverters [J]. IEEE Transactions on Power Electronics, 2003, 18(1): 140-150. [12] Mannen T, Fujita H. Dead-time compensation method based on current ripple estimation [J]. IEEE Transactions on Power Electronics, 2015, 30(7): 4016-4024. Analysis and compensation of dead-time effect in voltage source inverters considering parasitic capacitance and ripple current XIE Ye-yuan1, XIE Rui2, LI Cheng-min3, ZHOU Zhi-chao2, LI Wu-hua3 (1. NR Electric Co. Ltd., Nanjing 211102, China;2. Zhejiang Electric Power Design Institute Co. Ltd., Hangzhou 310013, China; 3. College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China) Inherent dead-time effect in voltage source inverters reduces the quality of output voltage. To eliminate the dead-time effect, the accurate mathematical model of error voltage caused by dead-time should be deduced firstly. However, state-of-the-art works on dead-time compensation do not consider equivalent capacitance of switches and ripple current at the same time, which leads to limited compensation efficacy. This paper finds out that these non-ideal factors have a significant influence on error voltage, and an accurate model of error voltage is thus established. Based on the analytical model, an online, adaptive compensation scheme is proposed. Experiment results verify the analysis and the validity of the proposed compensation method. voltage source inverter; dead-time effect compensation; parasitic capacitance; inductor ripple current; power quality 2016-08-04 谢晔源(1978-), 男, 江西籍, 高级工程师, 研究方向为柔性直流输电、 柔性交流输电和无功补偿技术; 谢 瑞(1979-), 男, 浙江籍, 高级工程师, 博士, 研究方向为智能变电站电气工程设计和电力电子技术。 TM464 A 1003-3076(2017)06-0016-06

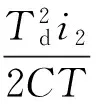
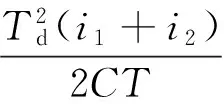
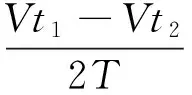

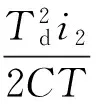

3 死区效应补偿方法
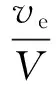
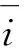
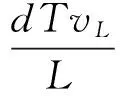


4 实验结果



5 结论

