基于PO算法的风电机塔架RCS快速求解

唐 波， 叶 莉， 孙 睿， 刘 任， 吴 卓

(三峡大学电气与新能源学院， 湖北 宜昌 443002)

基于PO算法的风电机塔架RCS快速求解

唐 波， 叶 莉， 孙 睿， 刘 任， 吴 卓

(三峡大学电气与新能源学院， 湖北 宜昌 443002)

对于工作在GHz频率下的电大尺寸风电机雷达散射截面(RCS)求解，传统采用的物理光学(PO)算法所需计算资源极为庞大，难以在风电机对雷达信号干扰评估的实际工程中进行应用。为减少求解占用的计算资源，本文提出了一种快速求解算法，即将风电机RCS求解分为两个部分：仍采用PO法计算叶片RCS；但采用近似法快速求解塔架RCS。计算时，将风电机塔架分割为一系列小的圆柱段，分别求解各独立圆柱段RCS，最后将各部分RCS进行叠加即可获得整个塔架RCS的计算公式。以Vestas V82风电机为例，结果表明采用快速求解算法计算得到的风电机RCS极大值偏差最大为3.15dBsm，全局极值最大相对偏差为5.14%，但计算资源减少88%。

风电机； RCS； 电磁散射； PO算法； 快速求解

1 引言

风电机对雷达信号的阻挡及散射现象将导致风电场区域附近的雷达性能退化，这种影响随着风电场建设规模的不断扩大而日趋显著。现有研究通常采用风电机雷达散射截面(Radar Cross Section， RCS)评估风电场对雷达台站的电磁干扰，因此，风电机RCS的准确快速求解成为干扰评估研究中的关键问题。

为准确求解风电机RCS，文献[1]采用矩量法进行计算。从理论上看，采用矩量法能够得到较精确的数值解，但由于风电机属于电大尺寸复杂散射体，造成文献[1]研究频率仅为20MHz，且只建立了简单的单片风电机叶片模型。为解决风电机RCS求解计算量过大的问题，现有研究通常采用物理光学法(Physical Optics，PO)[2]进行求解。随着研究的深入，用于求解RCS的风电机几何模型越来越精确。最初文献[3]将风电机叶片看作三角形金属平板，随后文献[4]将风电机叶片等效成圆柱体。文献[5-7]按照风电机的实际几何形状，提出了更加精确复杂的建模。上述风电机模型的不断精细化使求解精度越来越高，但同时导致计算量越来越庞大，乃至现有计算机硬件水平无法求解[8]。

风电机可以分为塔架、叶片、机舱3大部分。根据文献[9]的研究，塔架是风电机的最大散射源，其RCS值约占80%，而叶片RCS值仅占15%。因此，结合风电机塔架几何结构简单的特点，本文提出了将风电机叶片和塔架分开进行RCS求解的思想，即风电机叶片RCS仍采用常规PO算法进行仿真求解，但在保证一定计算精度的前提下，基于PO算法推导塔架RCS的近似求解公式，从而采取解析计算的方法替代塔架的精确建模仿真计算，解决风电机整体精确建模引起的计算量过大问题，实现工程应用中的风电机RCS快速求解。

2 基于PO算法的风电机RCS求解

2.1 雷达散射截面的概念

在物理概念上，雷达散射截面表征雷达目标截获和散射信号功率的能力。一般来说，目标几何尺寸越大，截获的来波功率越大；另一方面，空间不同方向上目标散射能力的大小与目标的形状有密切关系[10-12]。

风电机RCS是一种等效的面积，其大小与入射电场幅值的平方呈正比，与散射电场幅值的平方呈反比，且与雷达波的入射方向和散射接收机的方向有关。电磁波照射到风电机的总功率减去吸收和透射的功率，得到风电机截获的散射总功率，由此可以求得风电机RCS。

2.2 基于物理光学法的风电机RCS求解

物理光学法是目前求解风电机RCS的最常见方法，其原理是用散射体表面的感应电流取代散射体本身，通过对表面感应场的近似和积分而求得散射场。由于感应场保持有限，散射场也就同样为有限，这样就克服了平表面和单曲表面时场出现无限大的问题[13-15]。

物理光学法求解风电机RCS的过程如下：由雷达入射电磁波Ei求得风电机表面电流密度J，然后由J求磁矢量位函数A，再由上述计算得到的参量求解定积分方程获得散射场，最后由散射场强与入射场强的比值求得风电机RCS。

2.3 物理光学法在风电机RCS求解中存在的问题

采用物理光学法求解RCS时，风电机模型必须被剖分成小于1/3入射波波长的三角面元，剖分后平面单元的个数与频率的平方成正比[8]。随着频率的增加，计算的时间复杂度和空间复杂度几乎是几何级数增长，因此，采用PO法计算风电机RCS受到计算资源和存储空间的限制。

考虑到现有航空雷达工作在2.7～3.1GHz，航海雷达工作在9.1～9.41GHz，因此，在采用PO算法求解风电机RCS时，必须采用边长为厘米级的三角面元对高度达数十米、直径达数米的风电机模型进行剖分，从而造成计算单元的数量过于庞大，甚至难以求解。显然，减少剖分的面元数量是进行快速求解的关键，因此，可考虑对占RCS绝大部分贡献且又结构简单的塔架进行快速解析求解，从而避免PO算法中对风电机整体表面电流离散而形成大规模矩阵运算。

3 塔架RCS的快速求解

3.1 塔架RCS的快速求解思想

塔架是风电机最主要的散射体，且因为塔架属于对称且静止结构，故塔架RCS是一个与入射电磁波偏航角度无关的固定值[16]。因此，可对塔架进行PO近似解析求解，单独获取塔架的RCS。

算法的具体步骤是将塔架分割为N个等高圆台散射体，如图1所示。当N足够大时，每个圆台可视为独立的圆柱体，分别求解各散射体RCS，通过叠加计算可得到整个塔架RCS。这种方法避免了对风电机塔架表面的精细剖分，从而大幅缩短了计算时间；同时，当N达到一定值时，也可以保证计算精度要求。

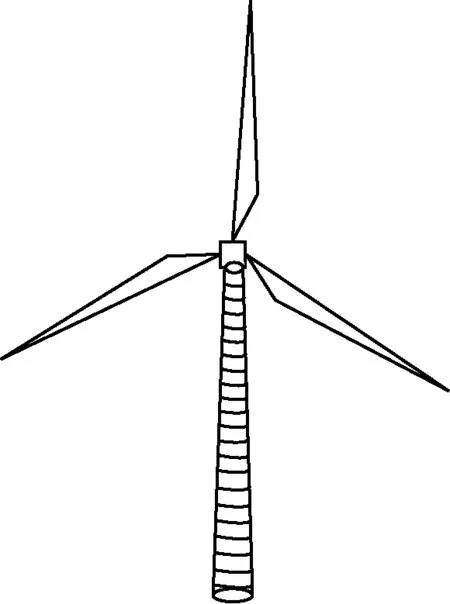
图1 风电机塔架分段模型Fig.1 Segmented tower model

在建模分析之前，需要进行下列2条假设：

(1)忽略大地对雷达电磁波的散射作用。

(2)由于各分段圆柱体直径比雷达信号波长大得多，故在求解塔架各分段圆柱体的相位时，其相位基准点位于各圆柱段中心。

3.2 圆柱体RCS的计算公式

文献[13]给出了任意散射体的RCS平方根物理光学表达式：

(1)

式中，k为自由空间波数，k=2π/λ，其中λ为波长；n为向外的曲面法线；er为接受装置电场极化方向的单位矢量；hi为磁场极化方向的单位矢量；r为散射体表面任意面元dS的位置矢量；i为入射波传播方向的单位矢量；s为散射方向的单位矢量。

当对象是圆柱体时，建立如图2所示的柱面坐标系O(r,φ，z)，在该坐标系下求解式(1)，从而得到圆柱体RCS的计算公式。

图2 圆柱体RCS计算数学模型Fig.2 Mathematical model of calculating cylinder RCS

表面面元由式(2)得到：

dS=adφdz

(2)

表面位置矢量r由式(3)得到：

r=r0+zz+an

(3)

式中，a为圆柱体半径；z为沿圆柱体轴向的单位矢量；r0为某一点到圆柱中心点的位置矢量。

将式(2)和式(3)代入式(1)，可得RCS平方根物理光学表达式：

φdz

(4)

将式(4)用轴向积分变量Iz和圆周方向积分变量Iφ表达可得：

(5)

式中

(6)

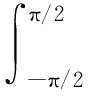
(7)

由式(6)可知，对于长度为L的圆柱体，其轴向积分容易由式(8)计算获得：

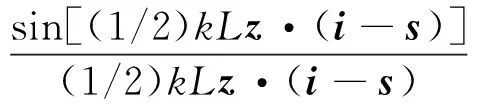
(8)

采用驻定相位法[17]计算沿圆周方向的积分变量Iφ，式(7)可得如下近似：

(9)

式中，n0为与轴线正交的向外曲面法线。

将式(9)和式(8)代入式(5)，对于单站雷达，雷达回波沿入射方向返回，因此，式(5)可简化为：

(10)

将式(10)两端取平方，得到独立圆柱体RCS的方程式如下：

(11)

式中，θi为侧向入射角度(如图2所示，其值用弧度表示)。

3.3 塔架RCS的求解公式

塔架总高度为L，将其分割为N个等高的独立圆柱段，各圆柱段长度用l表示，l=L/N。根据雷达高度和雷达范围，计算雷达到各部分距离d，从而计算各部分的相位。分段塔架几何结构如图3所示。

图3 分段塔架几何结构Fig.3 Segmented tower geometry

每个独立圆柱段RCS由式(11)获得，再近似求和得到整体塔架RCS。求和公式为：

(12)

式中，Δr=rn-rn-1，rn为第n部分圆柱体的半径，其值随着变量n从1～N不断变化。由此rn可表示为变量n的函数，其表达式为：

(13)

式中，r1为塔架顶端半径；r2为塔架底端半径。

当N取值极大时，各圆柱体尺寸极小，此时满足远场条件，入射电磁波近似为平面电磁波，故第n个圆柱体的RCS近似表达为：

σn=krnln2

(14)

将式(13)、式(14)代入式(12)，表达式化简为：

(15)

由式(13)可知，rn-rn-1=(r2-r1)/(N-1)，代入式(15)可得到直接由塔架最大半径和最小半径表示的RCS求解式：

(16)

最后，用式(16)替代式(11)中的kaL2，得到整体塔架RCS表达式：

(17)

综上，本文提出的快速求解步骤如下：利用近似算法计算风电机塔架RCS，塔架分段RCS值由式(11)获得，整体塔架RCS由式(17)求得；再利用传统PO法计算获得全部偏航角和旋转角下的机舱、叶片和前锥体RCS；最后叠加两部分RCS值求得整体风电机的RCS值。

4 风电机RCS求解示例

4.1 模型的建立

采用Vestas V82风电机进行RCS求解。塔架底端直径为3.65m，顶端直径为2.3m，塔架高度为77.5m，单个叶片长度40m。雷达的工作频率为3GHz。

图4(a)为风电机RCS求解模型坐标系。风电机叶片沿旋转轴旋转，旋转角不断变化，旋转平面为y-z平面。风向发生改变时，风电机的偏航角也随之改变。本文求解风电机偏航角从0°～360°变化下和风电机叶片旋转角从0°～120°变化下的风电机RCS值。

为验证所提算法的正确性，利用FEKO软件建立风电机模型，采用传统PO算法求解风电机RCS，并将其作为参考值。所建模型如图4(b)所示。

图4 风电机RCS求解模型Fig.4 Model for solving wind turbine RCS

4.2 计算结果及其分析

对Veatas V82风电机RCS进行快速求解，将计算结果与完整的PO模型计算结果进行分析比较。

图5为旋转角0°时，风电机RCS值随偏航角的变化趋势。由图5可知，快速解析求解的计算结果与完整风电机模型PO计算所得结果有着相近的变化趋势。在偏航角90°及270°左右，风电机与雷达属于侧对位置，风电机截获和散射的电磁波功率较小，故此时RCS出现极小值。

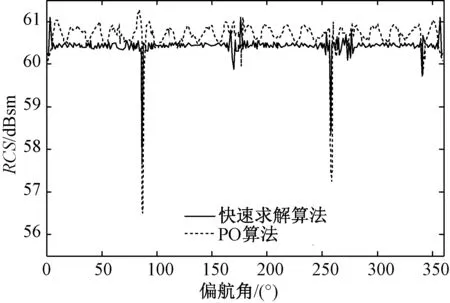
图5 风电机RCS值随偏航角度的变化(旋转角为0°)Fig.5 RCS variation around wind turbine (rotation angle is 0°)

另外，从图5可以看出，采用本文提出的算法得到的RCS值较传统PO法得到的RCS值小，这是因为相比于PO算法对塔架完整表面积的区域积分计算，对塔架进行快速求解时将塔架分段并将分段圆台近似成圆柱体，实际上减小了计算区域，也即减小了电磁散射的场源域，从而使得求解所得RCS偏小。同时，传统PO模型将整体风电机剖分成细小的三角形，能够精确地获取相位信息；而本文所提算法对塔架进行分段近似，即假设各独立圆柱段的相位参考位置位于各部分的中央，故近似法对塔架进行分段研究而未剖分是产生误差的主要原因。最后，由于将叶片RCS和塔架RCS相互独立，即忽略了叶片与塔架之间的电磁散射分量，从而使得两种算法的计算结果虽在趋势上大体保持一致，但其完整偏航角度内的数值波动幅值有一定差异。

图6为偏航角90°时，风电机RCS值随叶片旋转角的变化趋势。由图6可知，采用本文所提算法获得的结果与PO模型所得结果的趋势也基本一致，但极值及其出现的叶片旋转角度有一定的差异。快速求解得到风电机RCS值在旋转角20°时达到最小值59.21dBsm；在旋转角18°时达到最大值61.77dBsm。PO算法求得风电机RCS值在旋转角24°时达到最小值59.69dBsm；在旋转角17°时达到最大值61.19dBsm。这种差别主要由两种算法的根本机理引起， PO算法所获得的每个具体RCS值来源于不同旋转角下的风电机整体姿态求解，即每次计算时必须将叶片及塔架作为完整体系进行计算，从而充分考虑了叶片与塔架之间的相互作用；而采用近似算法，在偏航角度固定时，实际上固定了塔架的RCS，整体风电机RCS数值的波动仅来源于叶片的旋转。

图6 风电机RCS值随叶片旋转角度的变化(偏航角为90°)Fig.6 RCS variation with rotation (yaw angle is 90°)

4.3 误差分析

采用全局平均绝对偏差、全局极值最大相对偏差的概念[18]对快速求解所得风电机RCS的结果进行误差分析，从而验证算法的精确度。

全局平均绝对偏差计算公式为：

(18)

式中，σi为第i个角度下对应本文算法求解获得的RCS值；σi*为第i个角度下对应PO算法求解获得的RCS值。

全局极值平均绝对偏差计算公式为：

(19)

式中，σj为第j个极值点对应本文算法求解的RCS结果；σj*为第j个极值点对应PO算法求解的RCS结果；J为所有极值点所构成的集合。

全局极值最大相对偏差计算公式为：

(20)

4.1节算例中风电机RCS值随偏航角度和叶片旋转角度变化计算结果的全局平均绝对偏差、全局极值平均绝对偏差及全局极值最大相对偏差如表1所示。

表1 全局平均绝对偏差和全局极值最大相对偏差比较Tab.1 Comparison of mad, Δmax calculation results

可以看出，当旋转角为0°时，改变偏航角度，采用本文所提算法计算RCS结果与采用PO法计算结果最大相差3.15dBsm，全局极值最大相对偏差为5.14%；当偏航角为90°时，改变旋转角度，采用本文所提算法计算RCS结果与采用PO法计算结果最大相差1.53dBsm，全局极值最大相对偏差为2.50%。

将两种算法所占用的计算资源进行比较，传统PO算法占用的计算内存为151.95GB；而本文所提算法占用的计算内存为18.21GB。相较于传统PO算法占用的计算资源，本文所提算法占用的计算资源减少了88%，大大提高了求解风电机RCS的速度。

结合4.2节的数据分析，可以看出，对比本文提出的快速求解算法与PO算法，虽然部分风电机姿态下的RCS求解结果有一定差异，但整体风电机RCS的变化趋势相近，且极大值与全局极值最大相对偏差较小，因此可以用于风电机RCS特性的计算分析。同时，由于不需要对塔架进行精确建模计算，本文提出的算法所需计算资源与计算速度是常规PO算法无法比拟的。

5 结论

(1)以传统PO算法的计算结果作为参考值，针对3GHz激励下的Vestas V82风电机进行RCS求解，采用快速求解算法计算得到的风电机RCS极大值偏差最大为3.15dBsm，全局极值最大相对偏差为5.14%，但计算资源减少88%。

(2)本文提出的快速求解实际上将风电机分成了叶片和塔架两个相互独立的电磁散射场源，且将塔架RCS视为一个定值，因此该方法可用于工程中风电机RCS特性的快速分析，但无法用于风电机RCS的精确求解。

[1] Lewke B, Kindersberger J, Stromberger J, et al. MoM-based EMI analysis on large wind turbines[A]. Asia-Pacific Symposium on Electromagnetic Compatibility and 19th International Zurich Symposium on Electromagnetic Compatibility[C]. 2008. 196-199.

[2] Danoon Laith R, Brown Anthony K. Modeling methodology for computing the radar cross section and Doppler signature of wind farms[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(10): 5166-5174.

[3] Tennant A, Chambers B. Radar signature control of wind turbine generators[A]. IEEE Antennas and Propagation Society International Symposium [C]. Washington, USA, 2005. 489-492.

[4] Yucedag Senem Makal, Yucedag Okan Mert, Serim Huseyin Avni. Analytical method for monostatic radar cross section calculation of a perfectly conducting wind turbine model located over dielectric lossy half space[J]. IET Radar, Sonar and Navigation, 2014, 8(8): 965-970.

[5] La Tran Vu, Pennec François Le, Vaucher Christophe. Small wind turbine generic model design for BTS radio interaction studies[A]. IEEE 24th International Symposium on Personal, Indoor, and Mobile Radio Communications [C]. London, UK, 2013. 866-870.

[6] Belmonte Aniceto, Fabregas Xavier. Analysis of wind turbines blockage on Doppler weather radar beams[J]. IEEE Antennas and Wireless Propagation Letters, 2010, 9: 670-673.

[7] Gallardo-Hernando B, Munoz-Ferreras J M, Perez-Martinez F, et al. Wind turbine clutter observations and theoretical validation for meteorological radar applications[J]. IET Radar, Sonar and Navigation, 2011, 5(2): 111-117.

[8] 贾洪涛，张志军(Jia Hongtao，Zhang Zhijun).基于计算机图形学、物理光学法的RCS算法(RCS computation based on computer graphics and physical optics)[A]. 2009年全国微波毫米波会议论文集(上册)(Proceedings of the Microwave and Millimetre-wave Symposium of China)[C]. 745-747.

[9] Rashid L S, Brown A K. Radar cross-section analysis of wind turbine blades with radar absorbing materials[A]. Proceedings of the 8th European Radar Conference[C]. 2011. 97-100.

[10] 卢才成，洪家才(Lu Caicheng，Hong Jiacai).电磁散射的计算和测量(The Calculation and Measurement of Electromagnetic Scattering)[M]. 北京：北京航空航天大学出版社(Beijing: Beihang University Press)，2006. 21.

[11] 黄培康，殷红成，许小剑等(Huang Peikang，Yin Hongcheng，Xu Xiaojian，et al.).雷达目标特性(Radar target characteristics)[M].北京：电子工业出版社(Beijing：Publishing House of Electronics Industry)，2005. 2-5.

[12] 顾俊，王万富，童广德(Gu Jun，Wang Wanfu，Tong Guangde).引信目标RCS理论算法的发展及应用(Development and application of fuze target RCS theory in calculating method)[J]. 上海航天(Aerospace Shanghai)，2003, (4)：18-21.

[13] 欧紫娟(Ou Zijuan).基于CATIA建模的雷达引信目标RCS计算及应用(Calculation and application of radar fuze RCS based on CATIA modeling)[D]. 南京：南京理工大学(Nanjing: Nanjing University of Science & Technology). 2013. 6-7, 28-32.

[14] 聂在平，方大纲(Nie Zaiping，Fang Dagang). 目标与环境电磁散射特性建模：理论、方法与实现基础篇(Modeling of target and environment EM scattering characteristics: Theory, methods and fundamentals of implementation)[M]. 北京：国防工业出版社(Beijing: National Defense Industry Press)，2009. 117-180.

[15] 宋培茗(Song Peiming).雷达目标RCS的建模与检测(Modeling and detection of radar target RCS)[D]. 南京：南京理工大学(Nanjing: Nanjing University of Science & Technology)，2004. 15-17.

[16] Rashid L, Brown A. Partial treatment of wind turbine blades with radar absorbing materials (RAM) for RCS[A]. European Conference on Antennas and Propagation[C]. 2010. 1-5.

[17] 汪茂光(Wang Maoguang).几何绕射理论(Geometrical diffraction theory)[M]. 西安：西安电子科技大学出版社(Xi’an: Xidian University Press)，1994. 15-22.

[18] 蒋鸿林，张小苗，梁昌洪(Jiang Honglin，Zhang Xiaomiao，Liang Changhong). 基于有理函数逼近和MBPE结合恢复天线方向图(Combination rational approach and MBPE technology to resume antenna radiation patterns)[J]. 电波科学学报(Chinese Journal of Radio Science)，2005,20(6): 753-757.

Fast algorithm for solving wind turbine tower RCS based on physical optics

TANG Bo, YE Li, SUN Rui, LIU Ren, WU Zhuo

(College of Electrical Engineering & New Energy, China Three Gorges University, Yichang 443002, China)

For the electrically large size wind turbine (WT) operating at GHz frequency, the computational workload of WT RCS increases sharply using the Physical Optics (PO) method. Thus, the PO method can not be used in practical engineering for assessing WT interference with the radar signal. In order to reduce the computational workload, a fast algorithm is proposed by this paper, namely, the calculation of WT RCS is divided into two parts: the blades RCS is calculated using the PO method and the tower RCS is calculated using an approximation algorithm. This algorithm is developed by segmenting the WT tower into several small cylindrical sections, then solving each cylindrical section RCS independently. Therefore, the calculation equation of the whole WT tower RCS is acquired based on the superposition of RCS from each cylindrical section. Using a Vestas V82 WT as an example, this paper will demonstrate both PO algorithm and fast algorithm for calculating WT RCS. By comparing the results, it can be shown that the maximum deviation is 3.15dBsm, and maximum error is 5.14%. Nevertheless, the computational memory can be reduced by 88%.

wind turbine; RCS; electromagnetic scattering; PO method; fast solution

2016-07-21

国家自然科学基金项目(51307098)、中国电力科学研究院实验室开放基金项目(XT83-15-001)

唐 波(1978-)， 男， 湖北籍， 副教授， 博士， 研究方向为输变电系统电磁环境与超特高压输电技术； 叶 莉(1993-)， 女， 湖北籍， 硕士研究生， 研究方向为输变电系统电磁环境与超特高压输电技术。

TM723

A

1003-3076(2017)06-0076-07