三角函数的最值复习说课稿

广东台山市台师高级中学 陈艳红

设计教师：台山市台师高级中学陈艳红

教学年级：高三

授课时间：40 分钟

一、教学内容分析

三角函数的最值问题是三角函数基础知识的综合应用，是和三角函数求值问题并重的题型，是高考必考内容．

解这类题，不仅用到三角函数的各种知识，而且涉及到求最值的诸多方法，因而成为高考命题的热点．

二、教学目标分析

1.掌握三角函数最值的常见求法，能运用三角函数最值解决一些实际问题．

2.培养学生灵活运用公式、综合解题的能力。

3.培养学生分析、归纳、推理的能力。

三、一．二．教学重点难点分析

1.利用基本不等式求最值。

2.利用配方法求最值。

3.利用辅助角公式及有关函数关系式化简进行求最值。

四、教学方法分析

通过一些基本的正弦函数的有界性，先解决一些基本的问题，然后进行深化，过渡到较为复杂综合型的问题，主要培养学生的转化思想，由较繁的题目转化为熟悉的问题进行解决。

五、学法分析

在学法指导上，通过学生对于前面知识的回忆、结合，进行引导解题，学生在解题过程中不断思考，教师在解题中进行整理思路，力求学生在运用解题上掌握基本方法。

六、教学过程分析

本节课的教学流程是先由简答题引入，学生利用公式适当简化进行回答，然后提出主要题型，学生进行思考解题，教师在解题的同时进行题型的拓宽、深化，达到解题的迁移，同时掌握典例的解法，最后进行归纳，强调最值的基本解法。

七、教学内容安排

（一）主要知识

求三角函数的最值，主要利用正、余弦函数的有界性，一般通过三角变换化为下列基本类型处理：

①引入辅助角化为型，再利用正、余弦函数的有界性来求出其最值．

②，化为二次函数在上的最值求之．

③根据正弦函数的有界性，即可分析法求最值，还可“不等式”法或“数形结合”

（二）主要方法

①配方法；②化为一个角的三角函数；③数形结合法；④换元法；⑤基本不等式法。

（三）例题分析

例题1：当时，求的最值．

例题2：已知

求f(x)的最大值．

例题3：求的最值．

（四）巩固练习

（五）练习1：

已知

（1）求f(x)的最小正周期；

（2）求f(x)的最值

练习2：设函数f(x)=其中向量

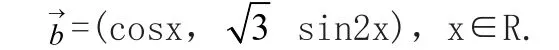
(1)求f(x)的取值范围

(2)若f(x)=1－求x；

练习3：当时,求函数的最大值和最小值。

练习4：求函数

f(x)=sinxcosx +sinx+cosx的最小值。

练习5：设a>0，对于函数下列结论正确的是（ ）

A、有最大值而无最小值

B、有最小值而无最大值

C、有最大值且有最小值

D、既无最大值也无最小值

八、教学小结

三角函数的最值问题，其本质上是对含有三角函数的复合函数求最值，因此求函数的最值方法都能适用，当然还有其特殊的方法。

三角函数的最值都是在限定区间取得的，因此要特别注意题设中所给出的区间。求三角函数最值时，一般要进行一些代数变换和三角变换，要注意函数有意义的条件，弦函数的有界性及变换的等价性。

九、课后作业

《走向高考》P78考例9的变式；P79“基础强化题” 第8题。

十、教学反思

在本节课教学中，可向学生渗透求三角函数的最值问题其实就是有关复合函数最值的问题，让学生站在较高的角度来理解这个问题，以便于更好的学习和理解。