“功能固着”对运用数学思想解题的困惑
——高三期末检测试卷讲评课片段实录
广东省深圳市第二实验学校 黄 云
一、问题的提出
“功能固着”是一类思维定势。就是当一个人熟悉了某种物体的常用或典型的功能后,就很难看出该物体所具有的其他潜在的功能。当需要利用某一物体的潜在功能来解决问题时,“功能固着”可能起到阻碍的作用。“功能固着”给学生在运用数学思想解题带来的主要影响有:函数与方程的不等价转化,转换与化归出现缺漏,数形结合出现偏差等。帮助学生消除“功能固着”心理,为更好地运用数学思想解题提供帮助。
二、困惑及成因分析
(一)运用函数与方程思想出现的困惑
在利用函数与方程思想时,学生不能将函数与方程(不等式)有机地联系起来综合考虑问题,受“功能固着”心理的影响,即便想到了函数与方程的结合,有时也不能简洁和完整的实施两者的等价转化,导致解题过程中思维受阻、无功而返或是出现不该出现的低级错误。
1.函数问题转化成方程问题不等价导致困惑
例1.已知函数若函数在上的值域是求实数m的取值范围。
困惑1:发现当x>0时,函数为增函数,后续没有了思路。
困惑2:将a,b看成方程的两个大于2的不等实数根,再对m>0和m<0来讨论一元二次方程的根,由于过程繁杂,无力继续,半途而废。
困惑3:就将a,b看作方程也即化简得的两个不等实数根,由解得答案不完备。
成因分析:困惑1属于知识结构不完整所造成的。要想办法将问题实施转化,构建关于m的不等式。困惑2属于不等价转换造成的。没有将a,b看作是方程的两个大于2的不等实根,忽视了函数的定义域;困惑3的产生是因为忽视了函数的值域。缺失对条件的挖掘,没能得出隐含条件m>0,导致讨论复杂化,没能求出实数的取值范围。 事实上,当x>0时,函数为增函数,a,b可以看作方程的两个不相等且大于2的实数根,由二次函数的零点的分布,令通过挖掘隐含条件得m>0,所以只需考虑一种情况m>0。当m>0时,易得即为所求。
2.方程问题转化成函数问题不等价导致困惑
例2.已知直线和双曲线的左支交于A,B两点,直线l过点和线段AB的中点M,求l在y轴上的截距b的取值范围。
困惑1:联立方程,利用中点坐标公式及由P,M均在直线上l,从而写出直线l的两点式方程并令x=0得l在y轴上的截距也可利用三点共线求得b,后续不知如何转化求解,到此而终。
困惑2:求得b后,
困惑3:求的最值,考虑定义域,即k的范围。由方程求得求得错误答案
成因分析:困惑1属于求解二次函数值域的方法不熟而受阻;困惑2没有考虑的定义域;困惑3面对于缺失考虑了为分母,没有去掉的情况导致错误。事实上,当求得时,还要兼顾为分母,剔除=0的情形,这样就能很容易获得正确的答案:b>2或
(二)运用转换与化归思想出现的困惑
利用转换与化归的思想可以化抽象为具体、化运动为静止、化复杂为简单、化陌生为熟悉,从而起到优化解题过程促进思维发展的作用。转换与化归也包括数学语言(文字语言、符号语言、图形语言)的相互转换,要剔除“功能固着”的影响,防止出现缺漏。
1.找不到转化点导致的困惑
例3.已知数列满足:
(Ⅰ)求数列的通项公式;
(Ⅱ)若数列满足:求数列的通项公式。
困惑1:熟悉求通项问题不知如何入手。
困惑2:由两式相减得的奇数项和偶数项分别是公差为4的等差数列,但后续求解作罢。
困惑3:利用条件来求bn,似曾相识,没有找到转化方法;采用“归—猜—证”的方法,没有找到规律,没能求出的通项公式。
困惑4:求得后将其代入得再用n-1替换上式的n,两式相减得,答案不全。
成因分析:困惑1属于思维受阻。无法实现转化;困惑2需要加强分类讨论的训练;困惑3 由与两式作差求bn,最快捷的办法,要注意否则会出错。事实上,(Ⅰ)法一:直接对进行配凑;法二:对分奇偶讨论;法三:采用“归—猜—证”,都可求得解答(Ⅱ)的思路有:其一,用n-1替换n两式相减,注意n≥2。 其二,采用“归—猜—证”求bn,排除后b1=7,从b2开始找规律,很快获得答案。
2.找不到化归点导致的困惑
例4.设函数上至少存在一个零点,求的最小值。
困惑1:至少存在一个式成立,即在上至少有一个实数根,对a>0和a<0讨论来确定a,b再求的最小值。难以进行。
困惑2:将方程改写为转换角度看问题,即为原点O到点直线上任意点找不到转化路径。
成因分析:困惑1没有将问题实施有效的转换,需要加强对问题的化归转换能力的培养。 困惑2能成功地将问题实施了有效的转化,变换主元将二次方程化归成了一次方程,很有价值!但后续没能找到如何将转化为的函数的路径。事实上,为原点O到点直线上任意的距离,如图1所示过原点O作直线的垂线,垂足为Q,有转化为t函数,所以因为需求最小值即可。两种基本方法:其一,求导;其二,对换元转化,都可求得
(三)运用数形结合的思想的困惑
数形结合包括“以形助数”和“以数解形”。利用这一思想能使问题直观化。 受“功能固着”的影响,许多学生在“以形助数”中,容易出现对应的图形不全面、不精确、不等价而导致困惑;而在“以数解形”中,会在设置数量关系构建代数模型上产生困惑。
1.“以形助数”的不完备出现困惑
例5.记集合
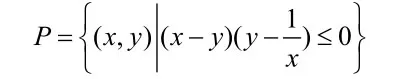
Q =表示的平面区域P分别为区域Q和区域,表示的平面区域为区域M,若向区域Q内撒一枚幸运小花朵,则花朵落在区域M内的概率为_________。
困惑:作出区域Q、P和M,作图不完备,导致结果错误
成因分析:要能准确完备地画出P和Q所表示的区域,如图2所示,表示的平面区域M为图中阴影部分,根据对称性,求得概率是
2.“以数解形”的不纯粹出现困惑
例略。
三、感悟与体会
在利用数学思想解题过程中,教师要帮助学生消除解题过程中产生“功能固着”心理的不利影响,培植正确使用数学思想解题的能力。要让学生明白:函数与方程问题要扣住“两个优先”即函数定义域优先和方程根的范围优先考虑。在使用转换与化归思想解题时,要让学生清楚:转化的目标是什么?谨防转化缺漏。在实施数形结合过程中,要确保数形互化的完备性和纯粹性。在教学中重视数学思想的渗透与培养,是提升学生综合素养的关键之所在。

