一元方程实数解定理
2017-06-19 11:29:04广西建工集团第四建筑工程有限责任公司南宁分公司
卫星电视与宽带多媒体 2017年16期
广西建工集团第四建筑工程有限责任公司南宁分公司 蒙 醒
16世纪,意大利数学家卡丹和费拉里分别提出了一元三次方程和一元四次方程求根公式。19世纪,挪威数学家阿贝尔证明了高于四次的一元方程一般没有根式解。本文构造的一元方程可以高于四次方,用传统的方法求该方程的实数解比较麻烦,用作者提出的定理求解则较为简捷。
一、一元方程实数解求根法

在的基础上乘以一个数或除以一个数、加上一个数或减去一个数、前面的数的m次方混合起来得到

在的基础上乘以一个数或除以一个数、加上一个数或减去一个数、前面的数的m次方混合起来得到

在的基础上乘以一个数或除以一个数、加上一个数或减去一个数、前面的数的m次方混合起来得到
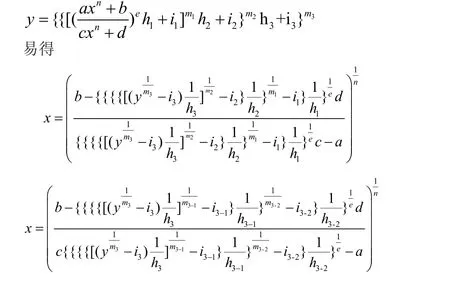

由上述可以看出以上是
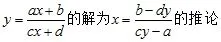
推论 方法2
的解为
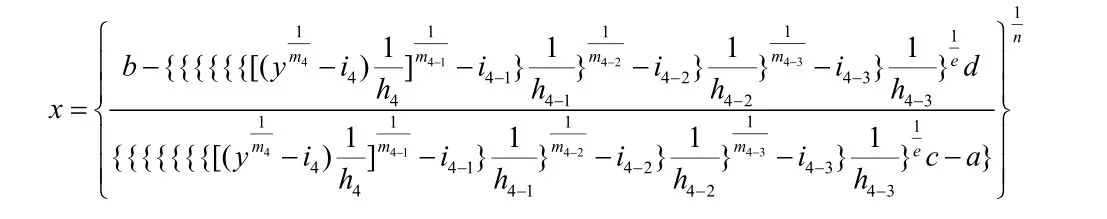
我将上述方程中的一组称为一组常数项,当最大的数q即p=2,3,4时,x的解中从左边第二组起最大的数q即p依次递减1,直至相减后的序号q都等于1。
二、一元方程实数解定理
在的基础上乘以一个数或除以一个数、加上一个数或减去一个数、前面的数的m次方混合起来再无限循环得到
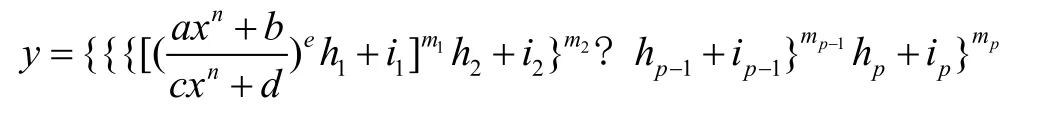
定理 a,c为常数且不全为零;b,d为常数且不全为零。和mq代替的数为正奇书,hq代替的数为常数且不为0。y和iq代替的数为常数。p≥4。(q是h,i,m的序号。hq,iq,mq分别代替一个数。p是q的最大数)

注 文章得到的解是实数解,需检验的最后进行检验即可。
证明:
当p=4时,
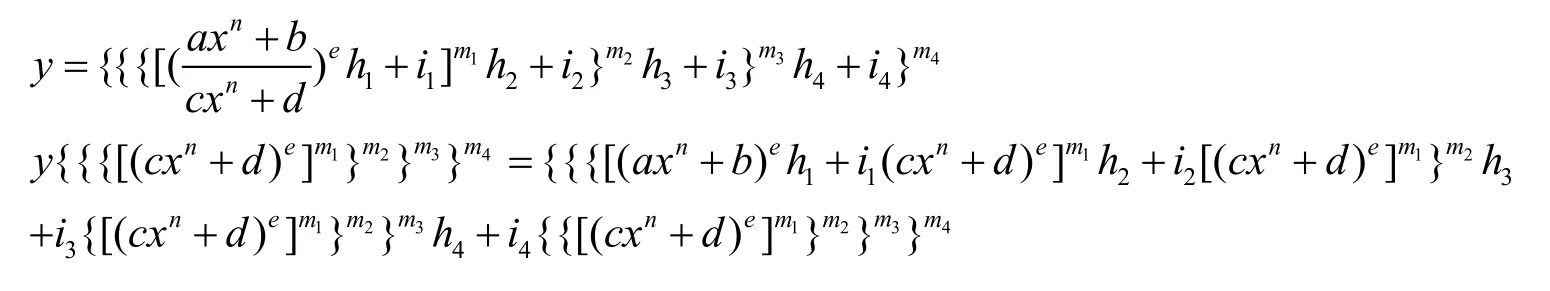
易得
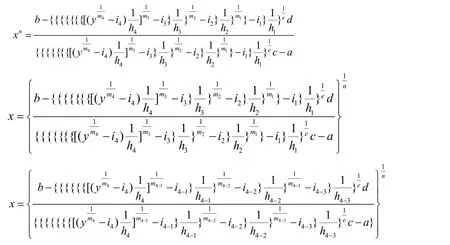
假设p=k(k≥4)的方程成立,即的解为:

那么当p=k+1时,
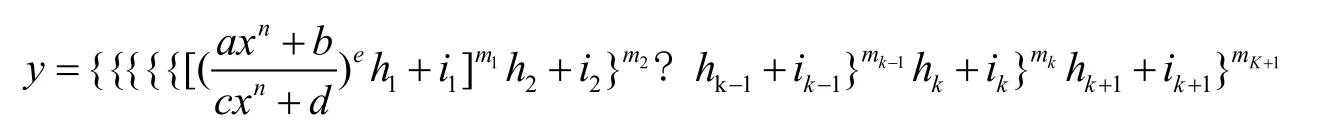
易得,

∴当p=k+1方程成立,
∴当p≥4时,定理成立。
结论:作者提出了一元方程实数解定理,并已证明。希望有关部门能将该定理收入教课书中,一来可以使学生增长知识,二来可以使学生提高学习的兴趣。
致谢:感谢余健英老师,杨秀前老师,李金汇好友,叶俊洋好友等提出的宝贵意见。
猜你喜欢
中学生数理化·七年级数学人教版(2023年3期)2023-03-21 00:45:16
中学数学杂志(初中版)(2020年6期)2020-01-06 03:35:20
新教育时代·教师版(2018年17期)2018-07-21 09:39:38
中学生数理化·七年级数学人教版(2018年3期)2018-05-30 06:58:13
祖国(2017年21期)2018-01-02 00:55:21
中学生数理化·中考版(2017年3期)2017-11-09 02:07:30
湖州师范学院学报(2016年2期)2016-08-21 13:50:52
Coco薇(2016年7期)2016-06-28 02:09:09
中学生数理化·七年级数学人教版(2016年2期)2016-05-30 21:20:57
作文·初中版(2015年10期)2015-10-26 16:37:53

