浅海中圆柱壳的声辐射特性分析
缪宇跃, 李天匀, 朱翔, 王鹏, 张冠军
(1.中国舰船研究设计中心,湖北 武汉 430064; 2.华中科技大学 船舶与海洋工程学院,湖北 武汉 430074; 3.船舶与海洋水动力湖北省重点实验室,湖北 武汉 430074; 4.高新船舶与深海开发装备协同创新中心, 上海 200240)
浅海中圆柱壳的声辐射特性分析
缪宇跃1, 李天匀2,3,4, 朱翔2,3,4, 王鹏2,3, 张冠军2,3
(1.中国舰船研究设计中心,湖北 武汉 430064; 2.华中科技大学 船舶与海洋工程学院,湖北 武汉 430074; 3.船舶与海洋水动力湖北省重点实验室,湖北 武汉 430074; 4.高新船舶与深海开发装备协同创新中心, 上海 200240)
根据声学边界元理论,本文在考虑海面和吸声海底的声反射作用基础上,对格林函数进行修正,建立波导域声辐射模型,并分析了浅海中圆柱壳的声辐射特性。研究发现吸声和刚性海底边界条件下圆柱壳的辐射声场有明显差别;可采用波导中点源格林函数预测圆柱壳的声辐射特性。结果表明边界反射作用随着圆柱壳离开海面或海底而减弱,随着场点离开圆柱壳而增强;且水深方向上声压呈周期性波动,其周期规律与海底边界类型无关。本文用声学点源的辐射叠加原理解释研究现象的产生机理,可为工程应用提供理论参考。
边界元;浅海;圆柱壳;声辐射;吸声海底;波导;格林函数;点源
有限空间中结构的声辐射特性往往不可避免地受到边界影响,其中半空间声辐射问题的研究较为成熟。黎胜等利用半空间声学边界元法研究了自由液面和刚性壁面对脉动球声辐射的影响,结果表明刚性壁面对脉动球辐射声功率的影响远小于自由液面对脉动球辐射声功率的影响[1-2]。邹元杰等建立了半无限流体域中结构流固耦合振动方程, 探讨了自由液面和刚性壁面对结构的固有频率、振动响应和有关声学物理量的影响,结果表明边界影响明显存在并随结构离开边界而减弱[3]。另外还有一些与半空间声学边界元法相关的文献,其重点在于流固耦合算法和半空间快速多极声学边界元法的研究[4-9]。陈炉云等对垂直和水平壁面同时存在的四分之一和八分之一空间声辐射问题展开研究,建立了多虚源的边界元模型,拓展了半空间声学边界元法的应用范围[10-12]。对类似平行波导的有限空间中结构声辐射问题的研究并不多见。邹元杰等建立浅水域声学边界元方程和相应的有限元/边界元流固耦合振动方程,研究平行边界对结构振动和声辐射的影响,其水底边界近似为刚性水底[13]。Chen等利用波叠加法研究了半空间和平行波导中结构的声辐射问题[14];Zou等采用三维声弹性理论分析了浅海环境对结构声辐射的影响,其中水底边界的反射系数为掠射角的函数[15-16]。白振国等采用解析法建立了浅水环境中二维圆柱壳的振动声辐射数学物理模型,研究了水深和浸深对圆柱壳声振特性的影响,结果表明圆柱壳离开水面一段小距离后其振动响应和表面声压与在无限水域中一致,边界对辐射声场的影响十分显著[17]。在浅海环境中(水深一般为几十到几百米),海底吸声作用不可忽略,本文首先对波导中格林函数进行修正,提出可考虑边界吸声作用的平行波导空间声学边界元法,然后研究吸声和刚性海底边界条件下浅海波导域中圆柱壳的声辐射特性及其规律,最后运用声学点源的辐射叠加原理解释辐射规律的产生机理。
1 海底吸声边界条件下的波导声学边界元法

(1)


图1 浅海平行波导空间中结构声辐射示意图Fig.1 The sketch of the acoustical radiation of structures in the shallow sea
平行波导空间中三维声学Helmholtz方程的基本解(格林函数)由实源项和虚源项叠加而成[13],可表示为
(2)
式中:第一项代表实源,第二项代表虚源,R0为P和实源Q的距离,RUn为P和虚源QUn的距离,RLn为P和虚源QLn的距离。FUn和FLn分别为QUn和QLn在海面和海底的反射系数,对于自由液面FUn=-1,对于刚性海底FLn=1。k0表示海水中的波数,m是与反射次数n相关的系数,m=j/2+[1+(-1)j+1]/4。
由于实源和虚源在一条直线上,QUn和QLn与Q的x坐标关系如下
(3)
式中:hU和hL分别为海面和海底到坐标原点o的距离,x0为Q的x坐标,h=hU+hL表示浅海深度。
实际上海底并非刚性,其对声波的吸收是很明显的。由于基本解中的三项e-ik0R0/(4πR0)、e-ik0RUn/(4πRUn)和e-ik0RLn/4πRLn分别表示位于Q、QUn和QLn的点源作用于场点P的声压,故式(1)表示分布于结构表面不同强度点源及其镜像在场点P的声压叠加[14-16]。在吸声边界条件下,点源格林函数中海底反射系数可表示为[19]
FLn=F+B
(4)
其中,
海水密度和声速为ρ0=1 025kg/m3和c0=1 500m/s,海底沉积层密度ρ1=1 400kg/m3,考虑沉积层对声波吸收的声速[20]c1=1 530(1-iη),其中η=0.021。
在结构表面划分边界单元,通过插值求得x0并代入式(3)得到xLn,则掠射角θn为
(5)
式中 xp是P的x坐标。
由式(4)和(5)求得反射系数FLn,再联合式(1)~(3)便可求得吸声海底边界条件下的浅海平行波导空间声场。在FLn中,当k0RLn足够大时可将B忽略,则FLn≈F。因为RLn随n的增大而增大,当hL=50m时,RLn≥50m。令k0=1rad/m,RLn分别取50、500、1 000m,其他参数同上。反射系数随掠射角的变化曲线如图2所示,其中反射系数由FLn和F的绝对值表示。
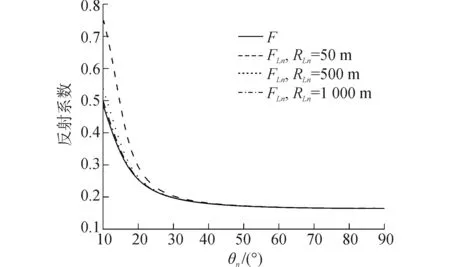
图2 反射系数随掠射角的变化曲线Fig.2 The variation of reflectances with the glancing angle
图2中FLn曲线随着RLn的增大而靠近F曲线,当RLn=500m时,两条曲线已经十分接近,RLn=1 000m时,两条曲线基本重合。同时可看出当掠射角超过30°后几条曲线几乎重合,所以在大角度掠射情况下k0RLn对反射系数的影响较小。由于在40°~90°区间内,反射系数下降非常缓慢,为方便收敛性分析及声场计算,此区间内反射系数可近似看作常数。
2 收敛性分析和算例验证
在Matlab中编程分析格林函数G的收敛性,设频率f=200 Hz和800 Hz,hU=10 m,hL=50 m,Q点坐标为(0, 0, 0),P点坐标为(0, 50 m, 0),格林函数幅值|G|随反射次数n的变化曲线如图3所示。

图3 格林函数收敛性曲线Fig.3 The convergence curves of green functions
由图3可看出吸声海底条件下的格林函数很快收敛,而刚性海底条件下的格林函数波动明显,收敛缓慢,这是因为两种海底边界的反射能力有很大差别,导致叠加效果不同。为保证收敛,在下文的计算中两种海底条件下的n分别取5和20。
在海底吸声边界条件下,以浅海平行波导空间中脉动球辐射解析解验证提出的声学边界元法的正确性。在脉动球表面划分若干个四边形单元,球心位于坐标原点o,f=200 Hz,场点分布为y轴上10~50 m的一条直线。此时FLn近似为常数,根据叠加原理[1]可知场点声压解析解为
(6)
式中:vn=1×10-6m/s,脉动球半径a=1m,r0为球心到场点的距离,rUn和rLn分别是球心在海面以上和海底以下的虚源到场点的距离。
图4展示了吸声海底条件下声学边界元法与解析法计算的声压级(SPL)曲线,可看出两种方法的结果十分吻合,证明所提方法是正确的。
3 浅海中圆柱壳的声辐射特性
简支在半无限障板上的圆柱壳模型如图5所示,圆柱壳长Lc=1.284 m,半径Rc=0.18 m,厚度为0.003 m,材料的杨氏模量为2.1×1011Pa,泊松比为0.3,密度为7 850 kg/m3。圆柱壳轴线与z轴重合,圆柱壳中心位于坐标系原点o,场点P在平面xy上,P到o的距离为r,γ为周向角。在圆柱壳下表面沿x轴施加频率为f,幅值为1 N的法向简谐激励力,激励力指向o。利用有限元法计算圆柱壳流固耦合模型的表面振速,当h=50 m时其均方振速在圆柱壳离开边界五倍半径距离后不再变化,这种情况与文献[17]研究结果一致。当h增大,边界影响将更小,故在h≥50 m情况下,圆柱壳离开边界五倍半径距离后可采用无限流域中圆柱壳的振速输入声学边界元Matlab程序中计算不同水深情况下圆柱壳的声辐射特性。

图4 脉动球场点声压级对比Fig.4 The comparison of the sound pressure level

图5 圆柱壳模型Fig.5 The model of cylindrical shell
设f=200 Hz,hU=10 m,hL=50 m,不同半径下的声压级指向性曲线如图6所示,其中SPLu、SPLa和SPLr分别表示忽略海底只考虑海面边界、海面+吸声海底和海面+刚性海底边界条件下的声压级。从图6可看出两种海底边界条件下的声压级指向性曲线总体上存在明显差别,SPLa曲线比SPLr曲线更接近SPLu曲线,这是因为吸声海底对声波的反射能力较弱。当hU和hL不变,r越大,SPLa和SPLr曲线与SPLu曲线的差别越大,这是因为不同场点处的叠加效果不同。

图6 不同半径下的声压级指向性曲线Fig.6 The directivity of the sound pressure level with different radius
令f=200 Hz,hL=100 m,r=15 m,浸深hU分别为50 m和200 m,且考虑静水压力作用,不同浸深下的声压级指向性曲线如图7所示,其中SPLi为无限流域的声压级。从图7可看出随着圆柱壳离开海面,SPLa曲线越来越接近SPLi曲线,这是因为圆柱壳离海底足够远,其反射作用可忽略,而海面的反射作用随浸深增加而减弱。再令hU=hL=50 m,声压级沿x轴的变化如图8所示。从图8看出,在圆柱壳下方三条曲线差别显著,SPLu曲线单调下降,而SPLa和SPLr曲线波动下降,并且SPLr曲线波动的剧烈程度远高于SPLa曲线;在圆柱壳上方三条曲线差别较小,波动情况相同。进一步发现,声压在任何情况下都表现出一种周期波动性,表明边界对声波的反射造成深度方向上出现驻波。波峰位置和波峰间距L并不因边界条件改变而改变,当f=200 Hz时波长λ=7.5 m,L=3.79 m,λ/L=1.98;当f=800 Hz时波长λ=1.875 m,L=0.94 m,λ/L=1.99,波长与波峰间距之比近似为一常数。
当hU=10 m,hL=50 m时,两种海底边界条件下的声压级分布云图如图9所示。从图9可见两种海底边界条件下的声压级分布有明显不同,吸声海底边界条件下的声压变化较小。在整个空间都有驻波分布,频率越高,驻波越密集,叠加声场中波峰波谷交错出现。
4 圆柱壳声辐射特性的产生机理
圆柱壳辐射声场中P点声压可以看作是无数个不同强度点源的辐射声压和反射声压在P点的叠加,式(2)中格林函数第一项幅值为G1,代表辐射声,第二项幅值为G2,代表反射声。当f=200 Hz时,设hU=10 m,hL=50 m,Q点坐标为(0, 0, 0),P点坐标为(0,y, 0);再设hL=100 m,P点坐标为(0, 15 m, 0),G1和G2随P点位置和浸深变化如图10所示。从图10看到G2/G1随着P点离开圆柱壳而增大,随着圆柱壳离开海面而减小,其根本原因是反射声与辐射声的成分比例随场点到虚源距离的变化而变化。

图7 不同浸深下的声压级指向性曲线Fig.7 The directivity of the sound pressure level at different submerged depths

图8 声压级沿x轴的变化Fig.8 The variation of the sound pressure level in the direction of x-axis


图9 声压级分布云图Fig.9 The nephogram of the sound pressure level

图10 G1和G2变化曲线Fig.10 The variation of G1 and G2
在结构声振问题中,半无限域和无限域指在某些条件下可以忽略某些边界的声波反射作用的情况。在浅海波导域中,当P点离圆柱壳较近和圆柱壳距离海面或海底足够远时,有可能忽略边界反射作用,在此情况下布置测点得到圆柱壳的辐射声压等同于半无限域或无限域测试结果。为寻找满足声学半无限域或无限域条件的P点,可采用点源格林函数进行预测,不同参数下的格林函数幅值如图11所示,其中Ga、Gu和Gi表示海面+吸声海底、忽略海底只考虑海面和无限流域中的格林函数幅值。从图11可见格林函数幅值的匹配情况与图6和图7中声压级的匹配情况完全一致,这点进一步解释了图6和图7所展示现象的产生原因,说明采用点源格林函数预测浅海中圆柱壳声辐射特性是可行的。

图11 格林函数幅值Fig.11 The amplitude of the green function
声压在深度方向上的周期性波动现象同样源自点源的声压叠加性。图1中实源和无限个虚源组成一条点源链,其中点源相位周期性变化。以构成一个周期的四个点源QU1、Q、QL1、QL2为例,设点源强度为A,则该周期的点源在P点的叠加声压为
(7)
当P点下降ΔR=λ/2时,P点的叠加声压变为

(8)
由式(7)、(8)和指数函数的周期性质可知,p0和p1具有相同的周期性,当| p0|为极大值时| p1|也为极大值,距离和边界条件的变化只改变幅值大小而不改变周期性,这便是λ/L=2的原因。
当只考虑海面反射作用时,实源和虚源组成相位相反的偶极子,P点的叠加声压为
(9)
当P点在实源和海面之间下降ΔR=λ/2时,P点的叠加声压变为
(10)
同样,p2和p3具有相同的周期性,当时| p2|为极大值时| p3|也为极大值,在实源和海面之间λ/L=2。
当P点在实源下方下降时,λ/L=2规律的产生条件便不再满足。此时RU1=R0+2hU恒成立,P点的叠加声压为:
(11)
可得到:
(12)
由式(12)可知| p4|随着P点下降而减小,故图8中SPLu在圆柱壳下方单调衰减。对应图8的格林函数幅值如图12所示(Gr表示海面+刚性海底边界条件下的格林函数幅值),从图12可看出格林函数幅值表现出与声压级相同的变化规律。以上现象是由流域边界对声波的反射作用产生的,而这点是早期圆柱壳声辐射问题研究文献并未关注的[21]。
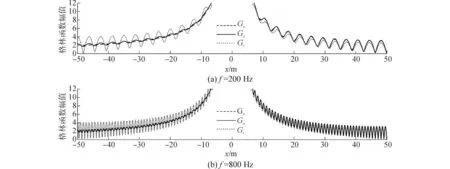
图12 格林函数幅值沿x轴的变化Fig.12 The variation of the green function in the direction of x axis
5 结论
1) 刚性和吸声海底边界条件下圆柱壳的辐射声压幅值有明显差异,吸声海底的声场叠加效果总体弱于刚性海底的声场叠加效果。
2) 可采用点源格林函数预测浅海波导域中圆柱壳的声辐射特性和寻找满足声学半无限域或无限域条件的场点,边界反射作用随着圆柱壳离开海面或海底而减弱,随着场点离开圆柱壳而增强。当圆柱壳与海面和海底距离满足一定条件时,其近场声辐射特性与半无限域或无限域中情况相同。
3)海面和海底对声波的多次反射在浅海波导域中产生复杂的叠加声场,波峰波谷交错出现,频率越高,驻波越密集,其中深度方向上的驻波遵循波峰间距为波长一半的规律,此规律不受边界类型影响。
[1]黎胜, 赵德有. 半空间内结构声辐射研究[J]. 船舶力学, 2004, 8(1): 106-112.
LI Sheng, ZHAO Deyou. Research on acoustic radiation in a three-dimensional half space[J]. Journal of ship mechanics, 2004, 8(1): 106-112.
[2]SEYBERT A F, SOENARKO B. Radiation and scattering of acoustic waves from bodies of arbitrary shape in a three-dimensional half space[J]. Journal of vibration and acoustics, 1988, 110(1): 112-117.
[3]邹元杰, 赵德有, 黎胜. 自由液面和刚性壁面对结构振动声辐射的影响[J]. 声学学报, 2005,30(1): 89-96.
ZOU Yuanjie, ZHAO Deyou, LI Sheng. Impact of soft surface and hard plane on structural vibration and acoustic radiation[J]. Acta acustica, 2005, 30(1): 89-96.
[4]ZHOU Q, JOSEPH P F. A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure[J]. Journal of sound and vibration, 2005, 283:853-873.
[5]BRUNNER D, JUNGE M, CABOS C, et al. Vibroacoustic simulation of partly immersed bodies by a coupled fast BE-FE approach[J]. Journal of the acoustical society of america, 2008, 123(5): 3418.
[6]JUNGE M, BECKER J, BRUNNER D, et al. FE-model reduction for FE-BE Coupling with large fluid structure interfaces[J]. Journal of the acoustical society of America, 2008, 123(5): 3726.
[7]CHEN P T, LIN C S, YANG T. Responses of partially immersed elastic structures using a symmetric formulation for coupled boundary element and finite element methods[J]. Journal of the acoustical society of America, 2002, 112(3): 866-875.
[8]JUNGE M, BRUNNER D, BECKER J, et al. Interface-reduction for the craig-bampton and rubin method applied to FE-BE coupling with a large fluid-structure interface[J]. International journal for numerical methods in engineering, 2009, 77(12): 1731-1752.
[9]ZHENG C J, CHEN H B, CHEN L L. A wideband fast multipole boundary element method for half-space/plane-symmetric acoustic wave problems[J]. Acta mechanica sinica, 2013, 29(2): 219-232.
[10]陈炉云, 王德禹, 张立军. 直角域内的结构声辐射特性研究[J]. 船舶力学, 2011, 15(1): 175-181.
CHEN Luyun, WANG Deyu, ZHANG Lijun. Research on acoustic radiation characteristic in a three-dimensional right-angle space[J]. Journal of ship mechanics, 2011, 15(1): 175-181.
[11]CHEN L, ZHANG Y. Acoustic radiation analysis based on essential solution of Green’s function[J]. Journal of Shanghai Jiaotong University: Science, 2013, 18: 409-417.
[12]CHEN L, LIANG X, YI H. Acoustic radiation analysis for a control domain based on Green′s function[J]. Applied mathematical modelling, 2016, 40(4): 2514-2528.
[13]邹元杰, 赵德有. 结构在浅水中的振动和声辐射特性研究[J]. 振动工程学报, 2005, 17(3): 269-274.
ZOU Yuanjie, ZHAO Deyou. A vibro-acoustic study on structures in shallow water[J]. Journal of vibration engineering, 2005, 17(3): 269-274.
[14]CHEN H, LI Q, SHANG D. Fast prediction of acoustic radiation from a hemi-capped cylindrical shell in waveguide[J]. Journal of marine science and application, 2014, 13(4): 437-448.
[15]ZOU M, WU Y, LIU Y, et al. A three-dimensional hydroelasticity theory for ship structures in acoustic field of shallow sea[J]. Journal of hydrodynamics, Ser. B, 2013, 25(6): 929-937.
[16]ZOU M S, WU Y S, LIU Y M. The application of three-dimensional hydroelastic analysis of ship structures in Pekeris hydro-acoustic waveguide environment[J]. Acta mechanica sinica, 2014, 30(1): 59-66.
[17]白振国, 吴文伟, 左成魁,等. 有限水深环境圆柱 壳声辐射及传播特性[J]. 船舶力学, 2014, (1): 178-190.
BAI Zhenguo, WU Wenwei, ZUO Chengkui, et al. Sound radiation and spread characteristics of cylindrical shell in finite depth water[J]. Journal of ship mechanics, 2014, (1): 178-190.
[18]CHEN L H, SCHWEIKERT D G. Sound radiation from an arbitrary body[J]. The journal of the acoustical society of America, 1963, 35(10): 1626-1632.
[19]ZAMPOLLI M, TESEI A, CANEPA G, et al. Computing the far field scattered or radiated by objects inside layered fluid media using approximate Green’s functions[J]. The journal of the acoustical society of America, 2008, 123(6): 4051-4058.
[20]汪德昭, 尚尔昌. 水声学[M]. 北京:科学出版社, 1981: 175-178.
WANG Dezhao, SANG Erchang. Hydroacoustics[M]. Beijing: science press, 1981.175-178.
[21]周锋, 骆东平, 蔡敏波, 等. 有限长环肋圆柱壳低阶模态声辐射性能分析[J]. 应用科技, 2004, 31(9): 38-41.
ZHOU Feng, LUO Dongping, CAI Minbo, et al. Sound radiation analysis of low order modes from the ring-stiffened cylindrical shells in fluid medium[J]. Applied science and technology, 2004, 31(9): 38-41.
本文引用格式:
缪宇跃, 李天匀, 朱翔,等. 浅海中圆柱壳的声辐射特性分析[J]. 哈尔滨工程大学学报, 2017, 38(5): 719-726.
MIAO Yuyue, LI Tianyun, ZHU Xiang, et al. Research on the acoustical radiation characteristics of cylindrical shells in ashallow sea [J]. Journal of Harbin Engineering University, 2017, 38(5): 719-726.
Research on the acoustical radiation characteristics of cylindrical shells in ashallow sea
MIAO Yuyue1, LI Tianyun2,3,4, ZHU Xiang2,3,4, WANG Peng2,3, ZHANG Guanjun2,3
(1.Ship Development and Design Center, Wuhan 430064, China; 2.School of Naval Architecture and Ocean Engineering,Huazhong University of Science & Technology, Wuhan 430074, China; 3.Hubei Key Laboratory of Naval Architecture & Ocean Engineering Hydrodynamics, Wuhan 430074, China; 4.Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration, Shanghai 200240, China)
According to the acoustical boundary element theory on acoustics and considering the sound reflection effect of the sea surface and sound-absorbing seabed, the Green Function was modified, and an acoustical radiation model in the waveguide domain was established. In addition, the acoustical radiation properties of a cylindrical shell in the shallow sea was analyzed. It is found that the sound absorption is apparently different from the radiative sound field of the cylindrical shell under the conditions of a rigid seafloor. The Green Function on the point source in the parallel waveguide space can be used to forecast the acoustical radiation of the cylindrical shell. When a cylindrical shell leaves the sea surface or seafloor, the boundary reflection effect will weaken; when a field point leaves the cylindrical shell, the effect will strengthen. In the direction of the water’s depth, the sound pressure fluctuates periodically, its periodic law is irrelevant to the type of seabed boundary. The radiation superposition principle of the acoustical point source is used to explain the formation theory of such a phenomenon, which can provide a theoretical reference for engineering applications.
boundary element method; shallow sea; cylindrical shell; acoustical radiation; sound-absorbing seabed; waveguide; Green function; point source
2016-01-15.
日期:2017-04-26.
国家自然科学基金项目(51379083,51479079,51579109);高等学校博士学科点专项科研基金项目(20120142110051).
缪宇跃(1988-), 男, 博士研究生; 李天匀(1969-), 男, 教授, 博士生导师.
李天匀,E-mail:ltyz801@ hust.edu.cn
10.11990/jheu.201601057
TB532
A
1006-7043(2017)05-0719-08
网络出版地址:http://www.cnki.net/kcms/detail/23.1390.u.20170426.1040.014.html

