混沌振动Lyapunov特征指数重构演化矩阵算法

刘树勇， 位秀雷，方远， 杨庆超

(海军工程大学 动力工程学院，湖北 武汉 430033)



混沌振动Lyapunov特征指数重构演化矩阵算法

刘树勇， 位秀雷，方远， 杨庆超

(海军工程大学 动力工程学院，湖北 武汉 430033)

针对Lyapunov指数计算过程中，邻近点对演化难以有效刻画混沌轨道在相空间不同方向的动态特性问题，本文研究了混沌重构相空间中映射矩阵的构造方法，推导了混沌振动实测时间序列重构相空间中Lyapunov特征指数演化矩阵算法表达式，分析了轨道演化过程中切空间级联矩阵对参考点邻域的拉伸折叠作用，揭示其特征向量方向是邻域变形的方向、奇异值大小对应特征方向上邻域拉伸和压缩的大小。构造了包含映射值域和定义域的增广矩阵，通过微扰法分析了计算过程的误差。计算结果表明，应用重构演化矩阵算法能够有效提取混沌时间序列最大Lyapunov指数。设计了非线性混沌振动实验装置，证实了该方法的有效性。

演化矩阵；切空间；投影算子；混沌；重构相空间；Lyapunov指数；混沌振动

混沌是机械、生物、物理、化学乃至社会、经济、大气等复杂系统中存在的普遍现象[1]。Lyapunov指数是实现混沌识别的重要指标。国内外学者对Lyapunov指数的计算进行了大量的研究。主要集中系统数学模型已知的情况下 Lyapunov指数谱[2-3]的计算以及直接从时间序列中计算Lyapunov指数。其中，WOLF等提出的时间序列最大Lyapunov指数的轨道追踪法对于计算该指数具有开创性的意义[4]。在该方法中，通过面积和体积的演化可以计算时间序列的所有Lyapunov指数谱。但该方法对轨道追踪有严格的要求，如：当两轨线的距离大于阈值时，需要重新搜索一个最近邻点，同时距离参考轨线的距离必须最小、与被置换向量方向之间的夹角尽可能小等。随后，KANTZ等提出了稳健的Lyapunov指数算法，通过追踪邻域的演化过程来进行计算指数值[5]；ROSENSTEIN等根据实测数据的特点提出了小数据量算法，其优点是在数据量较少时也可以实现对指数的计算[6]。随后，国内学者对小数据量最大Lyapunov指数计算参数选择提出了改进方法[7-8]，并探讨了多变量含噪声混沌时间序列Lyapunov指数的计算问题[9]。文献[10]提出了基于奇异值的Lyapunov指数计算方法，文献[11]则研究了基于智能网络的Lyapunov指数计算。但针对映射矩阵的重构技术和演化特征还缺乏深入研究，没有从本质上阐述映射过程中的物理含义。同时，实现时间序列Lyapunov指数的快速计算也是非常具有挑战性课题[12-13]。本文对演化矩阵重构方法进行了研究，并给出仿真和实验计算结果。

1 Lyapunov特征指数重构演化矩阵算法

1.1 相空间重构

1.2 演化矩阵的计算

图1 演化矩阵对邻域的变形作用Fig.1 The effect of evolution matrix on the neighborhood deformation

其中，φn是φ的第n次迭代。应用链式规则可以沿着系统的轨道估计出每一个步长的切映射，并得到n个切映射的乘积：

(1)

(2)

(3)

对于时间序列相空间重构吸引子而言，追踪重构轨道上参考点的邻近点或邻域的演化是计算Lyapunov指数谱的基本思想，如图2所示。但在计算过程中，切空间映射矩阵的计算和投影算子的重构规律还需要深入研究。

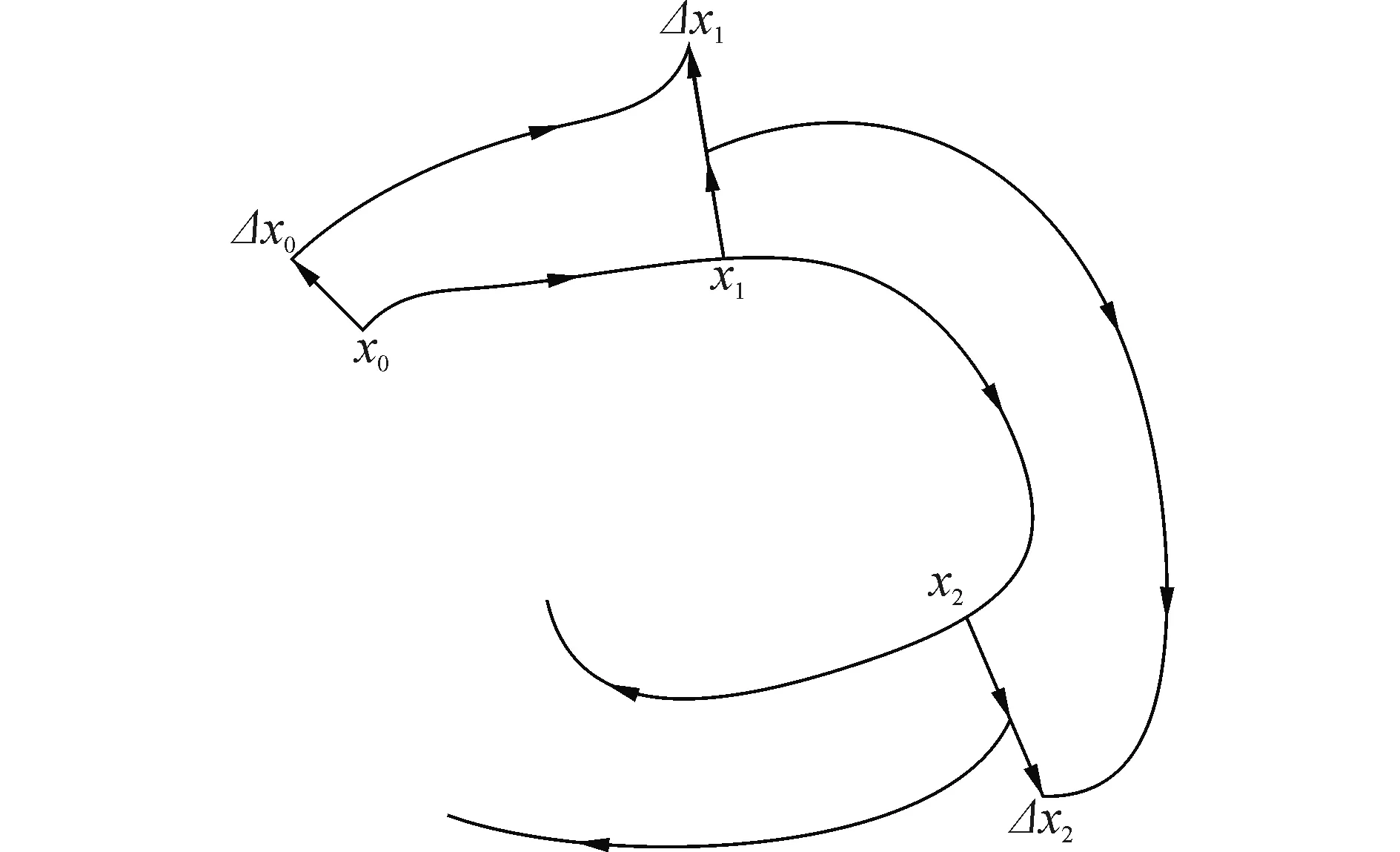
图2 重构轨道切空间的演化Fig.2 The evolution of reconstruction track tangent space

假设Δxi是在xi处切向量的近似，根据式(3)可得

(4)

{Δxi(jk)=xjk-xi|k=1，2，…，Nb}

(5)

由这些位移向量形成的矩阵记为邻域矩阵Bxi∈RNb×m。由于参考点和邻近点都随着相空间中的轨线不断演化，由此可以计算出经过一次演化后的位移向量：

{ΔXi+1(jk)=Xjk+1-Xi+1|k=1，2，…，Nb}

(6)

(7)

(8)

(9)

(10)

(11)

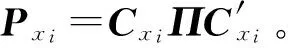
(12)

(13)

(14)

式(7)中的逆问题可以采取如下形式来描述：

(15)

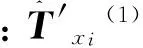
(16)

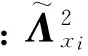
(17)

根据上面的分析可知，这种方法只需要采用m′×m′矩阵，而不需要m×m矩阵，使计算量减少。将式(15)改写成如下形式:

(18)

1.3 误差分析

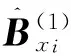
(19)

(20)

(21)

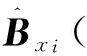
(22)

(23)

沿着相空间轨道计算出切映射矩阵后，进行

QR分解(QxjRxj)，得到Lyapunov指数谱的计算

(24)

式中:i=1，2，…，m；N是切映射矩阵演化次数。

2 Hénon混沌系统算例

以Hénon离散混沌系统为研究对象，其中，参数a=1.4，b=0.3，取3 000个点进行分析。

重构相空间过程，其延迟时间选择为1，得到其重构吸引子，如图3(a)所示。计算得到系统在重构相空间中的Lyapunov指数谱曲线，如图3(b)所示，在演化到400个步长时，曲线达到稳定。根据计算，得到不同嵌入维数时的Lyapunov指数谱，最大Lyapunov指数与标准值(0.408)的误差百分比如表1所示。从表中可知，该离散系统在嵌入维数合适时，计算误差很小。在嵌入维数增加过大时，会导致计算结果误差迅速大，需要通过相空间重构选择合适的维数。

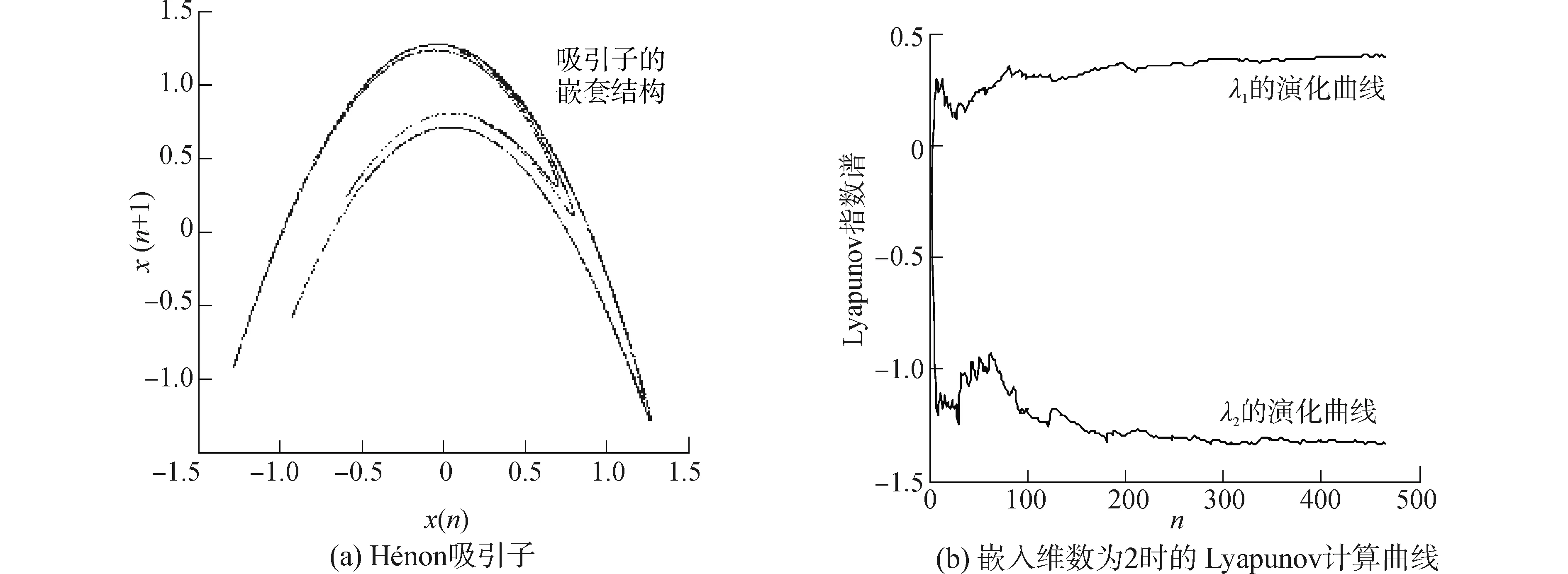
图3 Hénon系统仿真计算Fig.3 Simulation of Hénon

Table 1 Lyapunov exponents of different embedding dimension

嵌入维数Lyapunov指数最大Lyapunov指数与标准值[4]的误差/%20.4035,-1.33211.1030.3776,-0.7245,-0.1309-7.4540.4564,-1.1943,0.1008,-2.216311.86

3 Lyapunov指数计算实验研究

为了验证本文所提方法的效果，设计了单端磁吸式双势阱混沌振动试验装置，如图4所示，并对产生的混沌振动信号进行分析。该装置由如下部分组成：激振器、支座、板簧、磁铁、质量块、外部固定框架、固定板簧装置。各部件的具体功能为：1)激振器：提供稳定外部激励，保持整个系统持续稳定振动；2)支座：固定激振器，为了保证装置在水平方向上不受其他外力影响，需严格保持激振器水平放置；3)板簧：为整个装置的主体元件，为保证板簧具有良好的恢复力，刚度不易太硬，并且板簧的宽度不宜太小，这样可以减少其做水平摆动之外的运动；4)磁铁(方形磁铁)：提供板簧端部吸引力，固定磁铁的支座可以左右水平移动，进而调节磁力作用距离；5)质量块：安装在板簧自由端，受到磁力作用，它和磁铁一起形成了装置的双势阱，为保证板簧不产生水平摆动之外的运动，其质量不宜过大；6)外部固定框架：框架需满足两个要求，不能是磁性材料，以免对板簧运动形成外部干扰；质量不宜过大，否则难以保持整个框架的水平性，板簧的水平摆动会受到外部力的干扰；7)板簧固定装置：在两个夹紧螺母和板簧之间设置一个方形铁片，将螺母和板簧之间的点接触扩展成面接触，从而使板簧固定更牢靠。

图4 单端磁吸式混沌振动装置Fig.4 Two-well potential magnetic leaf spring chaotic vibration experimental rig

实验激励频率范围为5～25 Hz，采样频率为2 KHz，数据采集时长为5 s。调节功率放大器增益为0.96 V、激励频率为15 Hz时，采集数据并选择数据长度为3 000的信号段进行分析。由伪邻点嵌入维算法和第一最小互信息法[5]计算重构相空间参数中嵌入维数为3，延迟时间为10 s，得到的重构吸引子如图5(a)、(b)所示。

图5 实测信号的重构吸引子Fig.5 Reconstruction attractor of the measured signal

从图5中可以看出吸引子不同于极限环和二维环面等平凡吸引子。为了计算信号的Lyapunov指数谱，对轨道上的邻域进行分析，并重构演化矩阵。计算得到Lyapunov指数谱为(0.562 80，-0.012 5， -0.659 4)，如图6所示。由于最大Lyapunov指数大于零，因此表明所设计的系统处于混沌振动状态。

图6 重构吸引子上的邻域演化Fig.6 Neighborhood evolution of reconstruction attractor

4 结论

1)研究了重构相空间中映射矩阵的邻域构造法，推导了混沌振动实测时间序列Lyapunov特征指数算法表达式；

2)分析了切空间级联矩阵对参考点邻域的拉伸折叠作用，其奇异值的大小度量了初始距离的拉伸程度，其拉伸折叠的方向对应于演化矩阵的特征向量方向，矩阵奇异值涨落是导致邻域发生几何形变的内在动力；

3)设计了混沌振动试验台，并有效提取了实测信号的Lyapunov指数谱。数值计算结果和实测数据分析结果证明了该重构演化矩阵算法是切实可行的。

[1]LORENZ E N. A study of the predictability of a 28-variable atmospheric model[J]. Tellus， 1965， 17: 321-333.

[2]GREENE J M，KIM J S. The calculation of Lyapunov spectra[J]. Physica D， 1987， 24(1-3)： 213-225.

[3]BENETTIN G， GALGANI L， GIORGILLI A， et al. Lyapunov characteristic exponents for smooth dynamical systems; a method for computing all of them. Part 1: theory[J]. Meccanica， 1980， 15(1)： 9-20.

[4]WOLF A，SWIFT J B，SWINNEY H L，et al．Determining Lyapunov exponent from a time series[J]．Physica D，1985，16(3)： 285-317．

[5]KANTZ H， SCHREIBER T．Nonlinear time series analysis [M]．Cambridge：Cambridge Univ．Press， 1997： 65-74．

[6]ROSENTEIN M T，COLLINS J J，CARLO J D．A practical method for calculating largest Lyapunov exponents from small data sets [J]．Physical D， 1993， 65(1-2)：117-134．

[7]沈红兵，索洪敏．一种计算最大Lyapunov指数的改进小数据量法及其实现[J]．遵义师范学院学报， 2009， 11(6)： 73-75．

SHEN Hongbing， SUO Hongmin. A kind of calculating the improved small datum of the largest lyapunov exponent and its realization [J]. Journal of zunyi normal college， 2009， 11(6)： 73-75．

[8]杨永锋，仵敏娟，高喆，等．小数据量法计算最大Lyapunov指数的参数选择[J]．振动、测试与诊断， 2012， 32(3)： 371-374．

YANG Yongfeng ， WU Minjuan ， GAO Zhe， et al. Parameters selection for calculating largest lyapunov exponent from small data sets[J]. Journal of vibration， measurement & diagnosis， 2012， 32(3)： 371-374．

[9]陶慧，李莹，马小平．含噪声多变量混沌时间序列的最大Lyapunov指数计算[J]．河南理工大学学报：自然科学版， 2014， 33(6)： 770-775．

TAO Hui， LI Ying ， MA Xiaoping. Calculation for the largest Lyaponuv exponent of multivariate chaotic time-series with noise[J]. Journal of Henan Polytechnic University：Natural Science， 2014， 33(6)： 770-775．

[10]张晓丹，李志萍，张丽丽．一类基于奇异值分解的Lyapunov指数计算方法[J]．北京科技大学学报， 2005， 27(3)： 371-374．

ZHANG Xiaodan， LI Zhiping， ZHANG Lili. A method based on singular value decomposition for computation of Lyapunov exponent[J]. Journal of University of Science and Technology Beijing， 2005， 27(3)： 371-374．

[11]李冬梅，王正鸥．基于RBF网络的动力系统Lyapunov指数的计算方法[J]．信息与控制， 2004， 33(5)： 523-526．

LI Dongmei， WANG Zhengou. An algorithm for computing lyapunov exponents of a dynamical system based on RBF neural networks[J]. Information and control， 2004， 33(5)： 523-526．

[12]杨爱波，王基，刘树勇，等．基于空间栅格法的最大Lyapunov指数算法研究[J].电子学报， 2012， 40(9)： 1871-1875．

YANG Aibo， WANG Ji， LIU Shuyong， et al. An algorithm for computing the largest lyapunov exponent based on space grid method[J]. ACTA electronicasinica， 2012， 40(9)： 1871-1875．

[13]刘树勇，杨庆超，位秀雷，等．邻近点快速搜索方法在混沌识别中的应用[J]．华中科技大学学报：自然科学版， 2012， 40(11)： 89-92．

LIU Shuyong， YANG Qingchao， WEI Xiulei， et al. The application of fast searching nearest points method to chaos identification[J]. J. Huazhong Univ. of Sci.& Tech：Natural Science Edition， 2012， 40(11)： 89-92．

[14]蒋爱华，周璞，章艺，等．相空间重构延迟时间互信息改进算法研究[J]．振动与冲击， 2015， 14(2)： 71-74．

JIANG Aihua， HOU Pu， HANG Yi， et al. Improved mutual information algorithm for phase space reconstruction[J]. Journal of vibration and shock， 2015， 14(2)： 71-74．

[15]龙海辉，张佃中．基于等概率符号分析方法计算互信息确定延迟时间[J]．计算物理， 2010， 27(3)： 468-473．

LONG Haihui， ZHANG Dianzhong. Determination of delay time with mutual information by equal-probability symbolic analysis method[J]. Chinese journal of computational physics， 2010， 27(3)： 468-473．

[16]OSELEDEC V I. A multiplicative ergodic theorem Liapunov characteristic numbers for dynamical systems[J]. Trans. moscow math. soc.， 1968， 19(2)： 197-231.

[17]ULRICH P. Identification of true and spurious Lyapunov exponents from time series[J]. International journal of bifurcation and chaos， 1992， 2(1)： 155-165.

本文引用格式：

刘树勇， 位秀雷，方远，等.混沌振动Lyapunov特征指数重构演化矩阵算法[J]. 哈尔滨工程大学学报， 2017， 38(5)： 746-751.

LIU Shuyong，WEI Xiulei，Fang Yuan，et al.Study on the Lyapunov exponent algorithm based on the reconstruction matrices evolution[J]. Journal of Harbin Engineering University， 2017， 38(5)： 746-751.

A reconstruction evolution matrices algorithm based on Lyapunov characteristic exponent of chaotic vibration

LIU Shuyong， WEI Xiulei， FANG Yuan， YANG Qingchao

(College of Power Engineering，Naval University of Engineering，Wuhan 430033，China)

The reconstruction map matrix of chaotic phase space is studied since the dynamical characteristics of the chaotic orbit at different directions are discovered by the nearest orbit ineffectively， and the formulation of Lyapunov exponent based on evolution matrices in reconstructed phase space is derived. It explains that in the process of orbit evolution， the stretch and fold of the neighbor is the rotation operation of the cascade matrices and the fluctuation of the singular value of the reconstructed tangent space matrices. The SVD matrix of the reconstructed tangent space plays important role on the system dynamical behavior characteristic. The eigenvector direction is the deformation direction of the neighbor， and the stretch extent corresponds to the eigenvalue. The augmented matrix including range and definition domains is constructed， and the computation error is analyzed with perturbation. Numerical results show that the presented algorithm is useful to extract the maximal Lyapunov exponent of the chaotic time series. The experimental rig is designed and the Lyapunov exponent of the measured signal is computed with the method effectively.

evolution matrix; tangent space; projection operator; chaos; reconstructed phase space； Lyapunov exponent; chaotic vibration

2015-12-24.

日期：2017-04-27.

国家自然科学基金项目(5157942) ；国家自然科学基金青年基金项目(51509253)

刘树勇(1975-)， 男， 副教授; 位秀雷(1988-)， 男， 博士研究生.

位秀雷， E-mail:wxlcln@163.com.

10.11990/jheu.201512081

TN911

A

1006-7043(2017)05-0746-06

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20170427.1644.184.html