基于局部最优LWL的船舶操纵运动辨识建模

白伟伟， 任俊生， 李铁山， 李荣辉

(大连海事大学 航海学院，辽宁 大连 116026)



基于局部最优LWL的船舶操纵运动辨识建模

白伟伟， 任俊生， 李铁山， 李荣辉

(大连海事大学 航海学院，辽宁 大连 116026)

针对船舶操纵运动建模，本文提出了一种辨识建模方法，即局部最优的局部加权学习算法。该算法通过样本点重新排序和输入空间升维，解决了船舶运动状态一对多映射和不可分问题；并运用留一交叉验证为每个样本点训练一个距离测度，运用加权最小二乘在局部邻域中直接预测船舶操纵运动状态变量。构造局部目标函数，避免了传统的全局最优LWL算法容易陷入局部最优问题。与传统的机理建模相比，局部最优的局部加权学习算法克服了由多重共线性而引起的参数漂移和模型中存在未建模动态问题。通过一组人工数据和3自由度的Mariner轮的学习，实现了对非线性系统的高精度建模。与BPNN预报相比，具有较强的泛化能力。

局部加权学习；局部最优；距离测度训练；辨识建模；船舶操纵；一对多映射；未建模动态；局部目标函数

航海模拟器是船员培训、安全评估以及航海科研的一种重要平台，其核心为船舶运动数学模型。因此迫切需要建立高精度船舶运动数学模型[1]。

目前国内外船舶运动数学建模采用传统的机理建模方法，运用牛顿运动定律建立船舶运动方程，再采用试验[2-3]或者辨识[4-5]的方法解算出模型中的水动力导数。在解算模型过程中，运用很多假设和简化，例如假设船舶前后对称，忽略泰勒展开三阶以上的项等，造成模型中存在未建模动态。参数辨识能有效克服由于船模与实船雷诺数相差较大引起的尺度效应，但由于各个船舶运动状态之间存在一定的线性相关，导致参数辨识模型容易由多重共线性引起参数漂移。未建模动态和参数漂移使机理建模预报精度很难进一步提高。

以人工智能为代表的黑箱建模克服了传统基于机理建模的固有缺陷，代表性的方法有人工神经网络[6-7]、支持向量机[8-9]等。局部加权学习(local weighted learning，LWL)是一种典型的非参数学习方法，由William S. Cleveland于1979年提出[10]。LWL通过学习得到的系统参数为局部参数，针对不同的预测点学习到不同参数，因此能够有效克服传统参数模型存在的参数漂移问题。另外，LWL算法直接学习输入和输出之间的映射关系，不存在推导过程中对各种因素的忽略，能够有效避免未建模动态。

LWL算法的学习性能与距离测度紧密相关，距离测度决定高斯核函数核的大小，对确定邻域的大小和形状起决定作用。Müller等[11]估计了可变距离测度，常用的距离测度学习方法包括参数估计[12]、局部自适应[13]、梯度下降法[14]。然而，这些学习方法或者太复杂，或者存在陷入局部最优，很难应用于具有大惯性的船舶操纵运动。本文通过对系统输入空间升维，构造局部目标函数，提出了一种针对船舶操纵运动建模的局部最优LWL学习算法，解决了传统全局最优LWL算法计算复杂，预测严重非线性函数误差大以及有可能会陷入局部最优的问题。

LWL被广泛应用于各个工程领域，如机器人系统[15-16]、卫星遥感图像处理[17]等。LWL已经成为一种非常重要的非参数学习方法。本文在传统LWL算法基础上，提出了局部最优LWL辨识建模算法。首先通过样本重新排列将LWL算法适用于船舶操纵运动辨识建模；然后运用留一交叉验证为每个样本点训练距离测度；最后使用Matlab对Mariner轮建模验证。

1 船舶操纵运动数学模型及基础知识

1.1 Mariner轮船舶运动数学模型

船舶操纵水动力模型分为Abkowitz模型和分离型模型。本文拟学习Mariner轮的3自由度Abkowitz模型[18]，船舶运动方程如式(1)所示，该模型中的输入信号为舵角：

(1)

1.2 距离

LWL是一种局部逼近算法，对距离函数依赖程度较大。距离与邻域的大小形状和权值有直接关系，对样本点加权可视为对相似点的重视和放弃较远的点。一种简单的方法就是通过距离度量样本点和测试点之间的相似度。不同的工程领域可以采用不同的距离测量方法，如欧氏距离、马氏距离等。本文采用马氏距离：

(2)

1.3 高斯核函数

LWL算法通过核函数中核的大小来确定用于训练学习的样本点，其本质是为每个预测点确定一个学习邻域并建立一个局部模型。核函数(又称加权函数)是利用距离来计算每个样本点相对于预测点权重值，常用的加权函数是高斯核函数如下

K(d)=exp(-d2)

(3)

核函数通过距离测度来决定接受域的大小，通常距离测度有两种形式，一种是隐性距离测度，这种距离测度以矩阵的形式隐藏在距离矩阵中，本文采用另一种则是显性距离测度h：

(4)

通过h来调节邻域的大小更为直观方便，训练时更为简单方便。距离测度和邻域大小的关系如图1所示。其中，横轴为样本点据中心的距离，纵轴为权值。图中横轴0点代表预测数据点，以预测数据点为中心，随着h增大，接受域的半径逐渐增大。距离没有负值，符号用来表示不同的方向。

图1 核函数与距离测度的关系Fig.1 The relationship between kernel function and distance

1.4 目标函数

为了训练距离测度，将目标函数引入到LWL算法中，当目标函数值达到期望值时，停止训练。为了更好的得到预测点的输出，对目标函数进行加权：

(5)

(6)

1.5 留一交叉验证

Stone于1974年提出了交叉验证[19]。将数据集分为两部分，一部分用于训练，另一部分用于验证。与其他验证方法相比，交叉验证估计误差不需要任何假设前提。其中，留一交叉验证是一种使用最广泛的交叉验证法，其基本原理是留下一个样本点作为验证集，将其他剩余的数据作为训练集。

采用留一交叉验证法为每个样本点训练距离测度，即使单个点不能实现最优的训练结果，也不会影响整体的拟合效果，因此，该算法能很好的避免陷入局部最优问题，具有较强的鲁棒性。

2 LWL算法

船舶操纵系统输入包括当前时刻舵角，上一时刻运动状态和加速度，系统输出为当前时刻船舶运动状态和加速度。拟合的目标是寻找船舶操纵系统输入和输出之间潜在函数关系，一种方法是用样本点训练一种全局函数。然而，对于严重非线性的船舶操纵问题，很难找到一种函数逼近船舶操纵运动方程。另一种方法就是建立许多局部模型替代这种全局模型，LWL就是一种典型的局部逼近方法。

选择线性回归模型如下：

(7)

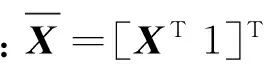
预测模型为

(8)

式中Xq为预测点输入。

首先，样本点减去预测点计算出样本点和预测点之间的距离，然后计算出样本点权值：

wi=K(d(xi，q))

(9)

权值方程采用式(2)和式(4)。权值是小于1的正数，大小随着样本点与预测点之间距离的增大而减小。另外，权值与距离测度也有关系。在迭代学习的第一步，式(4)中距离测度初值赋值一个较小的正数，构造初始拟合的局部邻域。随着距离测度的学习，该预测点的局部邻域逐渐改变。对样本点的输入矩阵X和输出矩阵y分别加权，构造以预测点为中心的局部邻域，如下：

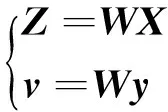
(10)

式中：zi、yi分别表示对样本点输入、输出加权处理，wj为权值按照式(4)计算得到，W=diag(w1，w2，…，wj)为权值矩阵。式(10)是对样本点加权，式(11)是对样本点矩阵加权。通过最小二乘法可以得到

(11)

则LWL对应预测点的预测值可得

(12)

式中：q是预测点的输入向量。由于船舶运动加速度非常小，且训练数据集中有相当一部分值为0，因此会造成(ZTZ)-1产生奇异。为了解决该问题，引入一个小的正定的设计参数矩阵Λ，这样不会改变(ZTZ)-1的特征值：

(13)

接下来，将按照目标函数式(14)来训练距离测度h。

(14)

依据式(14)目标函数值，对距离测度h进行学习更新。选择学习速率为λ：

h(k)=h(k-1)+λer(k-1)

(15)

3 LWL算法实例

本节中引入一组人工数据来说明本文算法的有效性，并与文献[15]中传统LWL算法拟合效果进行对比。拟合的任务是逼近如下函数：

(16)

式中：N(0，(0.05)2)是均值为0，方差为0.05的噪声。该函数是由两条相互垂直的窄长的脊和中心原点处的突起的高斯积层组成，如图2所示。在仿真时，训练数据集选取500个样本点，如图2所示。预测点均匀选取1 681个数据点。系统参数选择如下：λ=0.002，m=30 000，ε=0.000 000 1，h(0)=0.000 01。仿真结果如图2～5。

图2 目标函数形状图Fig.2 Target function to be approximated

从图3与图2的对比可以看出，两条垂直的脊和高斯积层都能拟合的很好，预测平均误差为0.023 9。文献[15]全局最优距离测度的结果如图5，仿真中选取500个样本点，其中两条脊拟合精度较低，高斯积层部分对比图4中的颜色，拟合效果也较弱，预测平均误差为0.039 9。本文算法拟合精度较传统全局最优算法提高了40.1%。图4中在图像四角出现了凹凸不平，这是由于算法中目标函数为局部目标函数，受干扰影响较全局最优LWL算法较大的原因，如能对数据进行预处理，减弱干扰则拟合效果更佳。

图3 预测结果Fig.3 Prediction result

图4 训练数据点分布情况Fig.4 Training data distribution

图5 全局最优拟合结果Fig.5 Global optimal fitting result

4 基于LWL算法的船舶操纵运动辨识建模

本文以3自由度的Mariner轮为仿真研究对象，学习文献[15]中的非线性水动力模型，并对比全局最优LWL算法验证本文算法在船舶操纵建模领域的有效性和优越性。本文所有操纵性仿真试验均是在MATLAB环境下进行的，配备主机频率3.2 GHz和4 GB运行内存。

4.1 船舶运动状态特性

LWL算法在机器人控制领域实现了可靠的、成功的应用。然而，船舶运动与机器人运动存在本质的区别：

1) 一对多映射关系。船舶输入舵角改变与船舶运动状态改变不是一一映射关系，以舵角与纵向速度改变为例，当舵角改变为某一定值时，船舶由于大惯性，纵向速度会逐渐变化经过较长一段时间稳定在某一定值，致使一个舵角值对应多个不同纵向速度。这种特性使船舶运动从根本上不同于机器人运动，通常表现为对系统对输入响应的时滞。这种特性是数学意义上的一对多映射关系。

2) 非线性特性。当船舶在小舵角范围内操纵时，船舶运动状态通常表现为线性。当船舶在大舵角范围内操纵时，船舶运动状态表现为非线性。在不同的操纵范围，船舶运动状态表现为不同的运动特性，对于黑箱建模是一个难点。另外，船舶运动状态的各个变量在数量级上差别比较大，例如，纵向速度的数量级为10 m/s，而纵向加速度的数量级为10-2m/s2。因此，在训练时，针对不同的状态变量采用不同的标准，如，在训练纵向速的距离测度时，选取ε=0.000 01，在训练纵向加速度时选取ε=0.000 1。

3) 船舶运动状态的不可分特性。船舶运动状态改变，如纵向速度，不仅是由于输入的改变，如舵角，还与其他运动状态改变有关系，如横向速度、转首速度。这种现象一般称之为耦合现象。另外，船舶在做Z形操纵试验时，船舶运动状态呈周期性变化趋势。对于一个特定的输入点，LWL算法并不能区分出上一时刻和下一时刻。这两种现象在本文中统称为不可分现象。解决该问题的一条简单、有效的途径是对系统输入空间进行升维，改变原有的映射关系并使系统学习船舶运动的趋势。因此，当前时刻的舵角，上一时刻的运动状态及加速度，三部分组成了本文算法的输入空间。

4.2 训练试验设计

本文试验过程中不考虑螺旋桨转速变化。初始船速为7.72 m/s。为了充分激励船舶运动特性，设计了一系列训练试验。首先是8字形试验。操纵时，首先向右舷操一定舵角，当船艏转过360°时，再向左舷操大小相同的反舵角，当船艏再次转过360°时，再次向右舷操大小相同的舵角，当船艏再次转过360°时，停止试验并记录试验过程中的舵角、速度变量、加速度变量。考虑到计算负担繁重，样本数据采样时间间隔选为2 s，测试试验数据采样时间间隔选为1 s，试验记录如表1前4组试验。为了进一步充分激励船舶运动特性，将Z形试验引入训练数据集，试验记录如表1后4组试验。为了验证本算法，测试试验中分别采用35°Z形试验和22°旋回试验，试验记录如表2所示。

表1 8字形和Z形训练试验记录

Table 1 The training experiment record from figure-of-eight and zigzag tests

编号舵角大小/(°)样本点数目1151032220948325935430895515219620242725264830300

表2 Z形测试试验记录

4.3 船舶操纵仿真结果

本节对比给出局部最优LWL和全局最优LWL算法的船舶操纵运动仿真结果以及BP神经网络预报仿真结果。为了减少计算机内存的占用率，横向速度和转首速度两个变量使用同一组距离测度预测。局部最优LWL算法参数选择如下：Λ=diag(0.001，0.001，…，0.001)，该矩阵维数与训练样本点总数相同为4 826。训练纵向速度选取λ=0.1，h(0)=0.5，m=50 000，ε=0.000 01；训练横向速度和转艏速度选取λ=0.1，h(0)=0.005，m=100 000，ε=0.000 01；训练纵向加速度选取λ=0.01，h(0)=0.005，m=100 000，ε=0.000 1；训练横向加速度选取λ=0.01，h(0)=0.005，m=100 000，ε=0.000 1；训练转艏加速度选取λ=0.01，h(0)=0.005，m=10 000，ε=0.000 01。BP神经网络选取三层隐层，节点数分别为s1=10，s2=15，s3=10。

下面将给出表2中测试试验的仿真结果。测试试验1的仿真结果如图6所示。从结果可以看出，LWL算法能够很好的预测训练数据以外的测试数据。这一性质是由LWL算法的本质决定，LWL算法能够很好的预测训练数据以外性质相似的数据，并获得良好的学习效果。最大误差指整个预报过程中出现的最大误差。最大误差时间点指最大误差出现的时刻，初始时刻为0。平均误差指整个预报试验点的绝对误差的平均值。平均误差百分比指平均误差占测试平均绝对值的百分比。从表3的误差定量分析可知，预测误差较小。从平均误差来看，加速度误差约为速度误差的3～5倍，这是由于加速度部分数值接近0，数值较小造成的。对比表4中全局最优LWL仿真结果，局部最优LWL仿真结果优于全局最优LWL。Z形试验船舶运动状态非线性较为严重，图6中全局最优LWL的学习误差主要表现在非线性严重的部分误差较大，这是由于全局最优LWL算法的在全局使用同一个距离测度的原因。尽管BPNN的预报仿真具有精度高，逼近非线性映射能力强的优点，图6(a)～(c)及图7中部分非线性映射BPNN较难实现准确的预报。在本文研究中发现，BPNN由于泛化能力弱，很难实现操纵性建模，对比给出BPNN预报结果充分说明本文算法的泛化能力较强。

表3 局部最优LWL测试试验1误差定量分析表

Table 3 Local optimal LWL error quantitative analysis of test experiment No.1

船舶运动状态最大误差最大误差时间点/s平均误差平均误差百分比/%u0.1088m/s490.0249m/s0.39v0.1797m/s880.0317m/s5.21r0.0030rad/s820.0004rad/s4.38u0.0042m/s280.0007m/s214.16v0.0065m/s250.0015m/s213.29r0.0003rad/s230.00004rad/s219.16

表4 全局最优LWL测试试验1误差定量分析表

Table 4 Global optimal LWL error quantitative analysis of test experiment No.1

船舶运动状态最大误差最大误差时间点/s平均误差平均误差百分比/%u0.0917m/s4470.0473m/s0.75v0.1869m/s720.0476m/s7.82r0.0071rad/s110.0012rad/s11.9u0.0060m/s2550.0011m/s222.06v0.0322m/s280.0041m/s236.2r0.0008rad/s270.00008rad/s242.41

测试试验2仿真结果如图8、9。与Z形试验相比，旋回试验的非线性较弱。然而，根据表5误差定量分析结果，本文算法结果加速度平均误差并没有比Z形试验的小很多。这是由于试验进行到200 s之后，加速度信号变为定值约为0，计算平均误差时，分母不变，而分子一直增大造成平均误差偏大。另外，全局最优LWL算法的平均误差百分比要优于本文算法，这是由于全局最优LWL预测非线性较弱的试验时整体误差较小。由于非线性较弱导致全局最优LWL的距离测度较大，这就造成了全局最优LWL在非线性部分的仿真结果误差偏大，主要表现为最大误差较大。即全局最优LWL的非线性映射学习能力较局部最优LWL弱。BPNN预报结果在线性部分较好，图8(a)～(c)初始阶段非线性部分预报效果较差，这是由于BPNN的泛化性较弱，对比说明本文算法的泛化性较强。

图6 35° Z形试验结果对比Fig.6 The comparison results with 35° zigzag test

加速度信号数量级较小，且有部分加速度数值趋于从上述仿真试验结果可以看出，LWL是一种针对船舶操纵运动建模的有效地学习算法。通过Z形试验和旋回试验的仿真操纵取得的良好效果可以看出LWL算法可以很好的学习到船舶操纵运动的特性。此外，LWL可以对训练数据集一定范围以外特性相似的数据进行很好的预测，这表明该算法具有一定的泛化能力。由表3～6可以看出，加速度变量仿真平均误差偏大，这是由于0造成平均误差百分比偏大。

图7 35°Z形试验操纵结果Fig.7 35° zigzag manoeuvring result

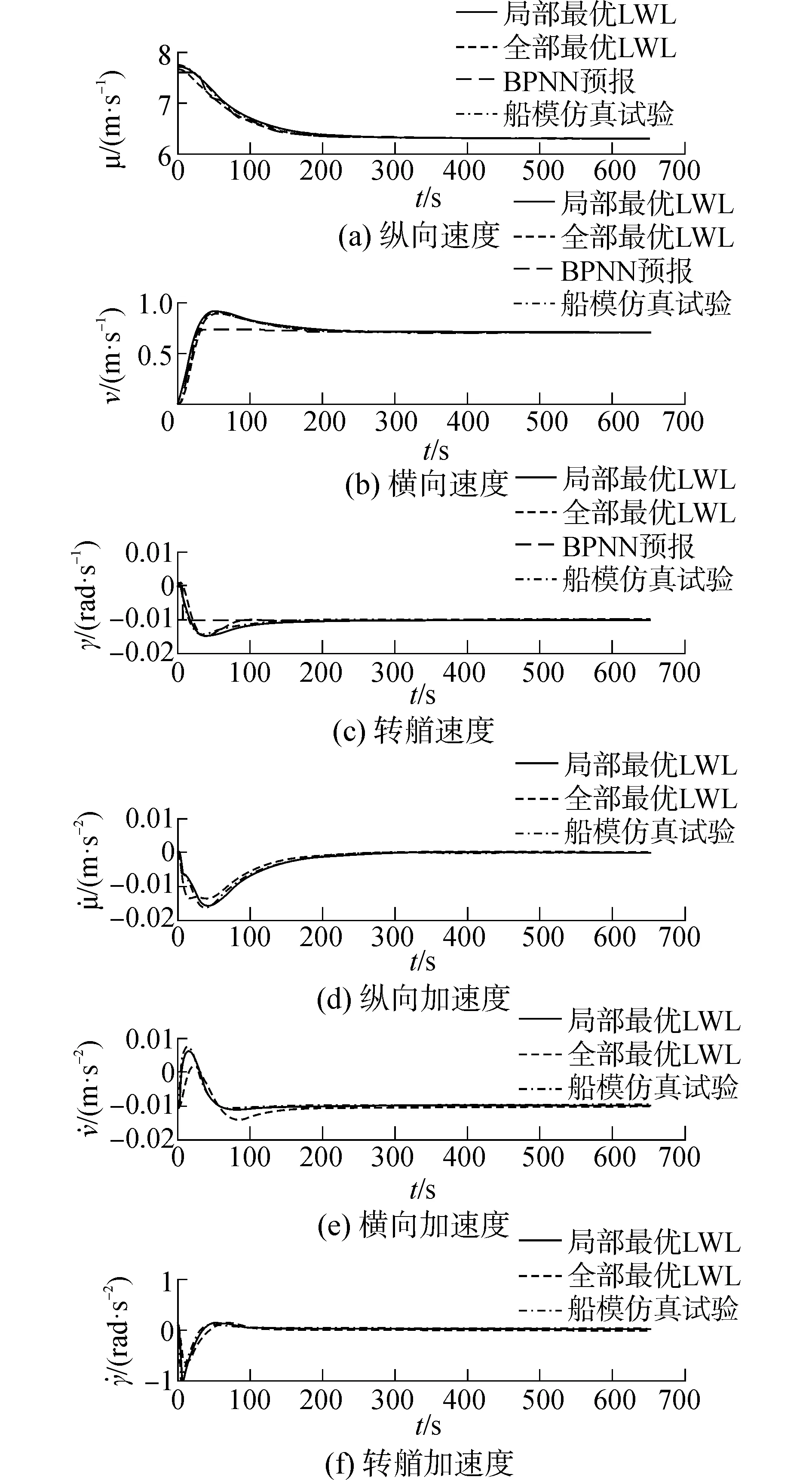
图8 22°旋回试验结果对比Fig.8 The comparsion with 22° turning test

图9 22°旋回试验结果Fig.9 22° turning manoeuvring results

Table 5 Local optimal LWL error quantitative analysis of test experiment No.2

船舶运动状态最大误差最大误差时间点/s平均误差平均误差百分比/%u0.0556m/s560.0130m/s0.20v0.0540m/s210.0052m/s0.71r0.0014rad/s130.0001rad/s1.3u0.0020m/s250.0002m/s210.7v0.0065m/s250.0002m/s211.76r0.0003rad/s230.00001rad/s232.71

表6 全局最优LWL测试试验2误差定量分析表

Table 6 Global optimal LWL error quantitative analysis of test experiment No.2

船舶运动状态最大误差最大误差时间点/s平均误差平均误差百分比/%u0.0702m/s260.0075m/s0.12v0.0948m/s160.0053m/s0.73r0.0052rad/s110.0004rad/s4.1u0.0060m/s2130.0002m/s29.9v0.0221m/s260.0017m/s297.69r0.0007rad/s250.00003rad/s290.37

5 结论

1)针对船舶操纵运动建模提出了一种基于存储在计算机中数据的离线辨识建模的局部最优LWL算法，克服了传统机理建模中存在的参数漂移和未建模动态问题。

2)在学习过程中，运用留一交叉验证法对样本点进行逐一训练学习，为每个样本点关联一个距离测度，通过这种学习方式避免了陷入局部最优，增强了算法的非线性映射能力。

3)通过提高输入空间的维度，解决了船舶运动状态的一对多映射和状态不可分问题，并取得了良好的预测结果。

4)仿真结果表明，LWL算法针对船舶操纵运动建模是一种强有力的工具，具有较强的泛化能力。

另外，本文算法在训练距离测度时选取初值只能依靠经验。LWL算法在每次计算时需重新确定参数，当数据量很大时，存在计算量较大的缺点，这是本文未来研究的重要方向。

[1]金一丞， 尹勇. 航海模拟器[M].北京:科学出版社， 2013: 9-10.

[2]FOSSEN T. Handbook of marine craft hydrodyna- mics and motion control [M]. New York John wiley and sons， 2011.

[3]YOON H， LONGO L， TODA Y， et al. Benchmark CFD validation data for surface combatant 5415 in PMM maneuvers-Part I: Force/moment/motion measurements [J]. Ocean engineering， 2015(109)： 705-734.

[4]SERGE S， SOARES C. An algorithm for offine identification of ship manoeuvring mathematical models from free-running tests [J]. Ocean engineering， 2014(79)： 10-25.

[5]ZHANG G， ZHANG X， PANG H. Multi-innovation auto-constructed least squares identification for 4 DOF ship manoeuvring modelling with full-scale trial data [J]. ISA transaction, 2015(58)： 186-195.

[6]YIN J， ZOU Z， XU F， et al. Online ship roll motion prediction based on grey sequential extreme learning machine [J]. Neurocomputing， 2014(129)： 168-174.

[7]孙洪波， 施朝健. 基于Elman网络的船舶运动模型辨识 [J]. 上海海事大学学报， 2014， 35(1)： 10-13.

SUN Hongbo， SHI Chaojian. Ship motion model identification based on Elman network [J]. Journal of Shanghai Maritime University， 2014， 35(1)： 10-13.

[8]WANG X， ZOU Z， HOU X， et al. System identification modeling of ship manoeuvring motion based on support vector regression [J]. Journal of hydrodynamics， 2015，27(4)： 502-512.

[9]XU H， SOARES C. Vector field path following for surface marine vessel and parameter identification based on LS-SVM [J]. Ocean engineering， 2016(113)： 151-161.

[10]WILLIAM S C. Robust locally weighted regression and smoothing scatterplots， Journal of the american Statistical association [J]. 1979， 74(368)： 829-836.

[11]MIILLER H G， STADTMULLER U. Variable bandwidth kernel estimators of regression curves [J]. The annals of statistics， 1987， 15(1)： 182-201.

[12]STANISWALIS J. Local bandwidth selectionfor kernel estimates [J]. Journal of the american statistical association， 1989， 84： 284-287.

[13]MICHAEL B， THEO G， EVA H. Locally adaptive bandwidth choice for kernel regression estimators [J]. Journal of the american statistical association， 1993， 88(424)： 1302-1309.

[14]STEFANT S， CHRISTOPHER G. Receptive field weighted regression [J]. ART human inf. process. lab.， kyoto， Japan， tech. rep. tR-H-209， 1997.

[15]STEFAN S， CHRISTOPHER G. Robot juggling: an implementation of memory-based learning [J].Control systems magazine， 1994， 14(1)： 57-71.

[16]STEFAN S， CHRISTOPHER G， SETHU V. Scalable techniques from nonparametric statistics for real time robot learning [J]. Applied intelligence, 2002，17 (1)： 49-60.

[17]MA J， JONATHAN C， FRANK C. Robust locally weighted regression for superresolution enhancement of multi-angle remote sensing imagery [J]. IEEE journal of selected topics in applied earth observations and remote sensing, 2014， 7(4)： 1357-1371.

[18]FOSSEN T. Guidance and control of ocean vehicles [M]. John wiley and sons， New York， 1994.

[19]STONE M. Cross validatory choice and assessment of statistical predictions [J]. J roy statist soc ser. B， 1974， 36:111-147.

[20]HWANG W. Cancellation effect and parameter identifiablity of ship steering dynamics [J]. International shipbuilding progress, 1982(26)： 90-120.

[21]张永库， 尹灵雪， 孙劲光． 基于改进的遗传算法的模糊聚类算法 [J]． 智能系统学报， 2015， 10 (4)： 627-635.

ZHANG Yongku， YIN Lingxue， SUN Jinguang. Fuzzy clustering algorithm based on the improved genetic algorithm [J]. CAAI transactions on intelligent systems， 2015， (04)： 627-635.

本文引用格式：

白伟伟， 任俊生， 李铁山， 等. 基于局部最优LWL的船舶操纵运动辨识建模[J]. 哈尔滨工程大学学报， 2017， 38(5)： 676-683.

BAI Weiwei， REN Junsheng， LI Tieshan， et al. Locally optimal-based LWL identification modeling for ship manoeuvring motion[J]. Journal of Harbin Engineering University， 2017， 38(5)： 676-683.

Locally optimal-based LWL identification modeling
for ship manoeuvring motion

BAI Weiwei， REN Junsheng， LI Tieshan， LI Ronghui

(Navigation College， Dalian Maritime University， Dalian 116026， China)

An identification modeling approach， locally weighted learning (LWL)， was proposed for ship maneuvering motion modeling. First， samples were rearranged， and the input dimension was raised to solve the one-to-multiple mapping and inseparability of the ship motion states; second， a distance metric was trained for every sample by the leave-one-out cross validation; finally， the motion states of the ship were directly forecast by the weighted least squares in the local neighborhood. By constructing a local cost function， the defect that the conventional global optimal LWL algorithm was easily caught in the local optimality was avoided. Compared with the traditional mechanism modeling， the method settles the problem of parameter drift caused by multicollinearity and the unmodeled dynamics existing in the model. The algorithm realizes high-accuracy modeling for nonlinear systems by learning a group of artificial data and 3-DOF of the mariner class vessel. Compared with the back propagation neural network (BPNN) prediction， the proposed scheme has improved generalization.

locally weighted learning (LWL); locally optimal; distance metric training; identification modeling; ship maneuvering; one-to-many mapping; unmodeled dynamics; local cost function

2015-12-24.

日期：2017-04-26.

国家高技术研究发展计划项目(2015AA016404)；国家自然科学基金项目(511090-20)；交通部应用基础研究项目(2014329225370)；海洋公益性行业科研专项经费项目(201505017-4).

白伟伟(1989-)， 男， 博士研究生； 任俊生(1976-)， 男， 教授， 博士生导师.

任俊生， E-mail: jsren@dlmu.edu.cn.

10.11990/jheu.201512082

U675.9

A

1006-7043(2017)05-0676-08

网络出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20170426.1040.016.html