巧赋妙解二项式定理问题

■江苏省仪征市南京师范大学第二附属高级中学 何晓勤

巧赋妙解二项式定理问题

■江苏省仪征市南京师范大学第二附属高级中学 何晓勤

赋值法是给代数式、方程或函数表达式中的某些字母赋予一定的特殊值,从而达到解决问题的目的。比如在解决与二项式定理有关的系数和、化简求值等相关问题时,我们就要对二项式定理中的字母进行赋值,下面举例加以说明,供同学们参考。

一、赋值解决与二项式系数和有关问题

证明:

(1)C0n+C1n+C2n+…+Cnn=2n;

(2)在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和。

分析:结合欲证等式的形式特征,需要在二项展开式中对字母a,b赋特殊值,如1和-1等。

解:(1)记(a+b)n=C0nan+C1nan-1b+

令a=b=1,即可得C0n+C1n+C2n+…+ Cnn=2n。

(2)在①式中,令a=1,b=-1,可得:

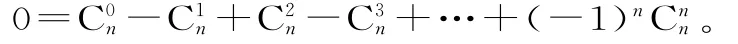
故C0n+C2n+…=C1n+C3n+…。②

故在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和。

点评:上述证明过程,通过对二项式定理中的字母进行赋值,得到与二项式系数的和有关的式子①和②。以上结论可以用来求解二项展开式的二项式系数的和及有关问题。

二、赋值解与二项式定理有关的化简问题

化简1-2C1n+22C2n-23C3n+…+

分析:观察该式的特征,可以发现该式应该为某式的二项展开式。

解:在(a+b)n=C0nan+C1nan-1b+C2nan-2· b2+…+Cnnbn中,令a=1,b=-2,可得1-2Cn1+22Cn2-23Cn2+…+(-1)n2nCnn= (1-2)n=(-1)n。

点评:在二项式定理中,赋予字母适当的值,即可得到很多相应的恒等式。

三、赋值解与各项系数和有关问题

已知(1-2x)2017=a0+a1x+…+ a2017x2017(x∈R),求下列各式的值:

(1)a0+a1+a2+…+a2017;

(2)(a0+a2+a4+…+a2016)2-(a1+a3+…+a2017)2;

(3)|a0|+|a1|+|a2|+…+|a2017|;

(4)a0+a2+a4+…+a2016。

分析:(1)式直接在原式中,赋x=1即可;(2)式可利用平方差公式,然后再分别赋x等于1和-1,联立起来求解即可;(3)式可先结合二项展开式的通项,判断各项系数的符号,再将目标式中的绝对值去掉,最后进行赋值;(4)式中欲消去展开式中的偶数项的系数,只需要在已知式中分别赋x等于1和-1,并将两式相加即可。

解:(1)在已知式中,令x=1,可得a0+ a1+a2+…+a2017=(1-2)2017=-1。①

(2)已知,(a0+a2+a4+…+a2016)2-(a1+a3+…+a2017)2

=(a0+a1+a2+…+a2017)(a0-a1+a2-a3+…+a2016-a2017)。

在已知式中,令x=-1,可得a0-a1+ a2-a3+…+a2016-a2017=32017。②

再结合①,可得(a0+a2+a4+…+ a2016)2-(a1+a3+…+a2017)2=-32017。

(3)已知(1-2x)2017的展开式的通项为Tr+1=Cr2017(-2x)r,则a2k+1<0,a2k>0,k∈N,k≤1008。

所以|a0|+|a1|+|a2|+…+|a2017|

=a0-a1+…+a2016-a2017=32017。

点评:求解展开式系数和的有关问题的关键是给二项式定理中的字母赋值,并进行适当的组合,赋值的选择则根据展开式的系数和形式特征来定。一般地,多项式f(x)=a0+a1x+…+ anxn的各项系数的和为f(1),常数项a0=f(0),偶次项的系数和为,奇次项的系数和为

四、先求导再赋值解决系数和有关问题

设(1-3x)5=a0+a1x+a2x2+

解:对(1-3x)5=a0+a1x+a2x2+a3x3+ a4x4+a5x5两边求导,则:

[(1-3x)5]'=-15(1-3x)4=a1+ 2a2x+3a3x2+4a4x3+5a5x4。

令x=1时,可得:

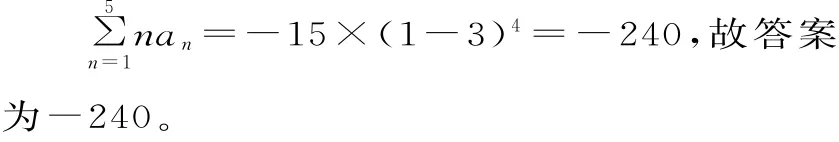
点评:解决本题的关键是先求导数,再利用赋值法来求解各项系数和,很多同学未能联想到导数,导致思维受阻。

(责任编辑 徐利杰)