经历比较过程，突出数位概念本质——“谁的红果多”教学思考

◇位惠女

经历比较过程，突出数位概念本质
——“谁的红果多”教学思考

◇位惠女

在进行北师大版教材一年级下册第三单元“生活中的数”集体备课时，老师们一致认为“谁的红果多”（百以内数的大小比较）这节课内容简单，学生不用教都会了，没有什么可备的内容。

首先，这节课的内容是在学生学习了百以内数的数数、读数、写数的基础上进行教学的，学生已经有了通过数数比较数的大小经验。其次，通过一年级上册学习20以内数的大小比较，学生已经积累了一定的数的大小比较的经验，老师们自然地认为内容好学。但是，老师们忽视了抽象地比较数的大小，对一年级小朋友来说，还是比较困难的。同时，此内容的学习并不仅限于学生会比较数的大小，更为重要的是借助这一载体，帮助学生进一步积累比较数的大小的经验，体会数位的意义，发展数感。

那么，如何从学生的已有经验出发，鼓励学生经历探索百以内数的大小的比较方法，突出 “数位”概念本质的教学呢？我进行了如下的教学尝试。

活动一：借助已有经验进行比较

课始，教师出示教材的情境图（如图 1），带领学生解读图意，提出“小熊和小猴，谁的红果多”的问题，鼓励学生自主探索百以内数的大小比较的方法。发现大部分学生都有了自己的想法后，再组织全班交流。

图1

师：我们来交流一下比较的方法，谁来说说自己的想法？

生1：我是用数数的方法，18、19、20、21，21在18的后面，所以是小熊的红果多。

师：谁和生1的方法一样？请举手示意一下。

此时，班里约有三分之一的学生举手，表示自己比较的方法与生1一样，即用数数的方法。这种方法，学生利用的是数数的经验，顺着数，后数到的数比先数到的数大，利用数的顺序直观比出数的大小。

生2：我觉得我的想法和生1差不多，但又有不同，我是在尺子上表示的（如图2）。

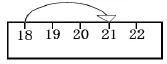
图2

师：谁能看懂生2的方法？

生3：他的方法是画了一截尺子，21在18的后面，很明显地看出来21比18大。

生4：这和我们以前在尺子上读数是一样的，先读18，再读21，所以21比18大。

师：还有谁也是通过画出这样的“尺子”来比较大小的？

在学习20以内数的认识时，教材借助尺子认识11~20各数，帮助学生体会20以内数的排列顺序，并比较大小，这样的学习经验自然延续到百以内数的学习。大约有5个学生采用了这样的方法进行比较，虽然还是数数的经验，却能借助“尺子”这个模型清楚地表达自己的想法，非常好。

师：谁还有不同的比较方法？

生5：我找20这个数作比较，21比20多1，18离20还差2，所以小熊的红果多。

生6：我的想法和生5一样，让20当中间人，比它大的数当然大了。

师：能明白他们的方法吗？谁有问题？

生7：我不太明白，为什么要找20这个数？

生5：20是个整十数，也正好在 18和21之间。

生8：19也在这两个数之间，为什么不用19这个数呢？

生6：（低头思考一会儿）我觉得19也行，但没有20方便，用两个数之间的整十数肯定更方便，一个少点，另一个过了，过了的数肯定大。

（生7点头表示同意生6的意见）

师：谢谢生7的问题，经过讨论我们更清楚了，20就是个“标准”，和这个标准进行比较，比标准大的数就大，所以是小熊的红果多。

在巡视中，发现借助“20”这个标准进行比较的学生不多，约有4人。寻找一个“标准”进行比较，是一种很重要的解决问题的策略。因此，我稍作停顿，鼓励学生提出问题，在问题交流中，确定“标准”必须是两个要比较数的中间的数，并逐步清晰什么样的“标准”比较方便，正如学生所言，19和20这两个数都行，但20是个整十数，比较方便。

活动二：借助模型进行比较

在学生自主探索比较方法的过程中，我发现有两个学生已经能借助直观模型方块进行比较了。借助这两个学生的方法，我们进入教材第2个问题的学习和讨论，主要交流过程如下。

师：有同学是这样比较的（如图3），你能看懂吗？

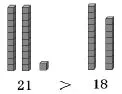
图3

生1：就是10个方块摞在一起，就变成1条了。21就是2条，再加1个小方块。

生2：1条就是 1捆小棒那样的，表示 1个十。

生3：18为什么也是摞在一起的2条？

生2：左边的1条是10个，表示1个十；右边的是8个，不到1个十，不能说是2条，只能说是1条，再加上8个小方块。

生4：这样一摆，可以清楚地看出来21里面有2个十，18不到2个十，21大于18，写成21＞18。

师：通过讨论，大家都明白了，下面请你利用学具摆一摆、写一写，并与同桌交流一下你是怎么做的。

在我看来，学生刚才的讨论是比较清楚的，要不要让学生再用小方块来摆一摆、说一说，我有点儿纠结，但学生的学习不能仅靠听别人讲是如何做的，自身去“做”非常重要。何况这里摆的小方块，要对应到计数器相应的数位上，教师需要帮助学生完成由直观到抽象的过程，把学生的数学直觉变得清晰准确。为此，我选择了让学生先摆一摆，再在计数器上拨一拨。

师：摆好后，再在计数器上拨一拨，说说你是怎么拨的。

生1：在摆的时候，21摆了2条零1个，我就在计数器的十位上拨2颗珠子，在个位上拨1颗珠子。

生2：18摆了1条零8个，对应在计数器上就是十位上1颗珠子，个位上8颗珠子。

师：也就是说，成条的方块对应的是计数器上的十位，单个的方块对应的是计数器上的个位。接下来，请你对照计数器写一写、填一填（如图4）。

（学生先独立完成，然后全班交流）

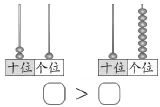
图4

生：我发现“21”十位上有2颗珠子，表示2个十；“18”十位上有1颗珠子，表示1个十。十位上2比1大，所以21＞18。

……

方块模型比实物抽象，但比计数器形象直观，在摆一摆、拨一拨、比一比的过程中，借助方块模型与计数器之间的连接，初步帮助学生从数位的角度来比较数的大小。

活动三：利用计数器进行比较

在教学教材上问题3（如图5）时，我还是选择了放手，直接出示问题3，鼓励学生先自主完成，再进行全班交流。

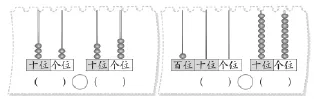
图5

从学生的学习情况来看，学生完成这两个小问题并不难，关键是如何让学生体会位值的价值，从数位的角度来比较数的大小。

师：我们先来交流左边的问题，谁来说说自己的想法？

生1：我写出的两个数是32与34。

生2：十位上都是3，是一样的，怎么比较呢？

生3：十位上的数一样的时候，可以看个位，个位上4比2大，所以34＞32。

师：谁同意生3的方法？

（大部分学生举手表示认同，个别学生有点儿犹豫）

生2：要是个位上的数也相同了怎么办？

师：你能举个例子说一说吗？

生2：都是32了怎么办？

生3：那就是相等的关系了，32=32。

（生2点头表示同意，其他学生自发鼓掌）

师：对于右边的问题，谁来说说自己的想法？

生4：右边的问题是比较100和99的大小。

生5:100比99大。

师：对，确实是100＞99，说说你的比较方法。

生6：考试的时候100分是最好的，比99分多（生笑），所以100＞99。

生7:100的最高位是百位，百位上是1，表示1个百，99的最高位是十位，百位上没有数，所以100＞99。

师：大家能明白生7的比较方法吗？谁再来说一说？

……

借助计数器比较两个数的大小，体会数位的重要性，为学生比较数的大小建立直观表象，积累比较数的大小的经验。

活动四：抽象的数的比较

数线是帮助学生建立数序、比较大小的重要模型。教材上问题 4（如图6）是利用数线上的数序，写出比45大的数，比90小的数，帮助学生体会100以内数的大小顺序。

在教学时，我先出示问题（如图6），鼓励学生独立利用数线图填写完成，再让学生说说自己的想法，重点进行了下面的交流。

图6

师：在填写的过程中，你有什么发现？

生：我发现45右边的数都比45大。

生：我发现90左边的数都比90小，右边的数就比90大了。

师：从数线上看，我们很容易就能发现45小于它右边的数，90大于它左边的数。想一想，如果没有图，该怎样比较两个数的大小呢？

生：我举个例子，如45＜□，可以看十位，十位上的数比4大就行。

生：我有补充，十位上的4不变的话，个位上可以是6、7、8、9。

生：先比十位上的数，十位上大的这个数就大，如果一样就比个位上的数。

生：我补充，100比99大，99百位上没有数，说明三位数比两位数大。

……

听着学生七嘴八舌的交流与讨论，我忽然失去了做小结的勇气，学生清晰的表达远远比我做小结重要得多。

数的大小比较的核心是位值制，无论是现今学生学习的整数大小比较，还是今后要学习的小数大小比较，看起来是位数、数位间的比较，实质上却是计数单位及其个数的比较。百以内数的大小的比较，看似简单，却是学生正式接触从数位的角度比较数的大小的开端，是学生后面学习大数之间比较的重要基础，来不得半点马虎。

（作者单位：河南省实验小学）