Decision-Making of a Single Supplier and Multiple Loss-Averse Retailers under Partial Trade Credit

WANG Zhihong(王志宏), LI Yue(李 悦), LI Hongguo(李红果)

Glorious Sun School of Business and Management, Donghua University, Shanghai 200051, China

Abstract: Under partial trade credit, suppliers usually require retailers to pay a fraction of the purchase cost immediately when ordering and the remaining payment is deferred at the end of the sales period. Considering a supply chain consisting of a risk-neutral supplier and multiple loss-averse retailers, we develop models under partial trade credit. We analyze the optimal decisions of a supplier and retailers under decentralized decision-making. The study shows that there is a unique Nash equilibrium among the retailers, and the optimal total order quantity of retailers increases as the delayed payment ratio increases and as the degree of retailers’ competition increases, but decreases with an increase in the loss aversion. Numerical studies are conducted to demonstrate the solution procedures and the effects of the parameters on decisions and profits.

Key words: partial trade credit; loss aversion; multiple retailers; decision; supply chain

Introduction

Trade credit is one of the most important short-term financing methods widely used by enterprises in different countries and regions such as China, the United States and Europe[1-4]. It is an effective incentive and coordination contract in supply chain management[5-7]. Suppliers provide trade credit to downstream retailers, which allows the retailers to postpone payment. Trade credit reduces retailers’ capital occupancy and encourages them to increase their orders. At the same time, suppliers receive more profits. In actual operation, suppliers usually require retailers to pay a fraction of the purchase cost immediately when ordering and to settle the remaining payment at the end of the sales period. This is partial trade credit. For example, Sany Heavy Industry Co., Ltd. offers partial trade credit to the dealership within the allowable credit period. Nowadays, partial trade credit is widely used in the engineering machinery industry in China[8-9].

Trade credit is facing an increasing number of uncertain factors that bring risks to the operation of trade credit and immeasurable losses to the supply chain. Capital-constrained and smaller enterprises tend to respond more strongly to loss and show characteristics of loss aversion, which will affect supply chain decisions. In addition, a single supplier often provides partial trade credit for multiple competing vendors simultaneously. Thus, how will multiple retailers’ competitiveness and loss aversion affect credit decisions and operation decisions in the supply chain? What will happen to the supply chain’s profits? These are the theoretical and practical issues of concern.

The operation management literature on partial trade credit mainly concerns the buyer’s inventory problem under given trade credit terms, where the economic order quantity (EOQ) model is adopted as one of the simplest and most basic inventory models in partial trade credit[10]. To develop EOQ models under partial trade credit, Zhouetal.[8]developed a synergic EOQ model by considering partial trade credit, shortages, imperfect quality, and inspection errors simultaneously. Rajan and Uthayakumar[11]built an EOQ model for instantaneous deteriorating commodities with inventory-level-dependent demand to obtain optimal replenishment policies under partial trade credit. Instead of setting trade credit as a given parameter, Wangetal.[12]developed a Stackelberg model from the perspective of the supplier. In the model, the supplier set a threshold for a trade credit policy, the proportion of payment for the order, and the discount factor for partial payment; then the retailer made the decision accordingly.

In recent years, Mahata[13], Soni and Joshi[14], Chenetal.[15], and Wuetal.[16]considered the two-tier trade credit (upstream full trade credit and downstream partial trade credit) in the perishable product supply chain consisting of a supplier, a retailer and a customer, and studied the retailer’s optimal replenishment decision. In contrast, Liaoetal.[17]investigated the optimal wholesaler’s replenishment decisions for deterioration items within the EOQ framework by assuming that the wholesaler obtained partial trade credit from the supplier, but the wholesaler offered full trade credit to the retailer，i.e., upstream partial trade credit and downstream full trade credit.

Several researchers have investigated three-level trade credit. Pramaniketal.[18]proposed an EOQ model under three levels of a partial trade credit policy, where a supplier, a wholesaler and a retailer offered some credit periods on some fraction of the total purchased amount to the wholesaler, the retailer and the customer, respectively. Pramaniketal.[19]developed an integrated supply chain model with price, credit period, and credit amount dependent on demand, where both the wholesaler and the retailer enjoyed the same full credit facility but the retailer only offered partial trade credit to the customers. For stochastic demand, Zhouetal.[9]determined the optimal order and payment decision of the retailer with different penalty rates given under partial trade credit when the retailer’s immediate payment ratio was exogenous and endogenous.

The existing studies on partial trade credit do not consider the loss aversion of decision makers and the situation where multiple retailers are involved in a supply chain. In order to fill these gaps in the existing literature, we explore the decision-making of a supply chain with a single supplier and multiple loss-averse retailers under partial trade credit. The main contributions of this study are in two ways. First, we formulate a Stackelberg game model in the case where a supplier offers partial trade credit to multiple loss-averse retailers, and analyze the Nash Equilibrium of retailers. The key distinction is that we incorporate the loss aversion of multiple retailers into the model. Second, we investigate the impact of the degree of retailers’ loss aversion, the retailers’ competition, and the fraction of delayed payment on the optimal decisions of retailers and the supplier.

The remainder of this article is organized as follows. Section 1 focuses on the parameters and assumptions of the model. Section 2 studies the optimal policies of retailers and suppliers under decentralized decision-making. A set of numerical experiments and analyses are conducted to illustrate the effectiveness of partial trade credit models in section 3. Finally, conclusions are drawn in section 4.

1 Parameter Settings and Assumptions

Consider a supply chain that consists of a supplier andnretailers, where the supplier is risk neutral and the retailers are loss averse. The retailers order the same product from the supplier at the beginning of each selling period and pay a certain proportion of the payment when ordering; that is, the supplier offers a certain partial trade credit to retailers. Then the supplier organizes production according to the total order quantity and delivers goods to the retailers on time. In the paper, the degree of retailers’ competition is described by the number of retailers, and more retailers mean more competition. The optimal decision variables are indicated by the superscript*.

Model parameters and variables are as follows.

λis the loss aversion coefficient of retailers;kis the proportion of the payment provided by the retailer immediately when ordering;k′ is the proportion of the payment delayed (0≤k′≤1, andk′=1-k);wis the unit product wholesale price provided by the supplier;cis the supplier’s unit product production cost;pis the retailer’s unit product sales price;sis the salvage value of unit product unsold (p>w>c>s);Qscis the total production under centralized decision-making;Xis the total random demand ofnretailers with probability density functionf(x) and cumulative distribution functionF(x);Xiis the random demand faced by the retaileriwith probability density functiong(xi) and cumulative distribution functionG(xi),i=1, 2, ...,n.

Model assumptions are as follows.

(1) Information shared between the decision makers in the supply chain is common knowledge.

(2) The working capital of the retaileriis [kwQi,wQi]; that is, the initial capital of the retaileriis not sufficient to cover the full payment, and the retailers assume limited liability.

(3)nretailers sell the same product and there is competition among them. Under decentralized decision-making, letQibe the order quantity of the retaileri,Q-ibe the order quantity ofn-1 retailers except the retaileri, andQ(Q=Qi+Q-i) be the total order quantity ofnretailers. We assume that the total demandXis divided among the retailers in proportion to their respective order quantity. Specifically, the demand of the retaileriisXi, and

We can get the following equations:

(1)

(2)

The demand allocation rule is known as the proportional demand allocation rule in Refs. [20-23]. As pointed out by Cachon[20], Wang[21]and Wuetal.[23], the proportional demand allocation rule is a reasonable model when customers have a relatively low search cost (e.g., online shopping) and the qualitative insights from this rule are consistent with other demand allocation rules considered in Ref.[24].

(4) We assume that the retailers are loss averse and consider a simple piecewise-linear form of a loss-aversion utility function.

where,ziis the expected profit of the retaileri;z0is the reference wealth level (decision reference point) of the retaileriat the beginning of the selling period；λ(λ≥1) indicates loss aversion coefficient of the retailer, the loss of the retailer is neutral ifλ=1, and greater values ofλimply higher levels of loss aversion. Without loss of generality, we normalizez0=0. This piecewise-linear form of loss aversion utility function has been widely used in behavioural economics and operations management literature (seen in Refs. [21, 25-27]) and is an approximation of the non-linear loss aversion utility functions presented by Tversky and Kahneman[28].

2 Decision-Making in the Supply Chain

2.1 Decisions of loss-averse retailers

According to the actual operation of partial trade credit, the supplier plays a dominant role in the supply chain. Consider a Stackelberg leader-follower relationship among the supplier and the loss-averse retailers, and a Nash game betweennretailers. Specifically, the sequence of events is as follows. The supplier determines the wholesale pricewand the proportion of delayed paymentk′ according to the loss aversion of retailers, and then retailers decide their individual order quantityQiaccording to the decision-making of the supplier and their own loss aversion.

As retailers are loss averse, their decision objective is to maximize the expected utility. In partial trade credit, in order to control their own risks, the supplier requires the retailers to pay part of the full payment when ordering, and allows the retailers to postpone the remaining payment (wQi-kwQi); that isk′wQi. At the end of the selling period, the income of the retailer including salespxiand the salvage value income of the unsold productss(Qi-xi) are used to pay the outstanding paymentk′wQi. Comparing the income of the retailer with its outstanding payment, the profit function of the retaileriis

Then we can express expected profit function of the retaileriasE[πri(Qi,Q-i)] and expected utility functionE[U(πri(Qi,Q-i))] as

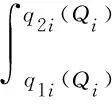
(3)

From Eq. (1) and Eq. (2), we rewrite and simplify Eq. (3) and obtain:

(4)

Theorem 1 Whens/w≤k′≤1, the retailerihas a unique optimal order quantityQi*that satisfies the following first-order condition:

(5)

Proof See APPENDIX A.

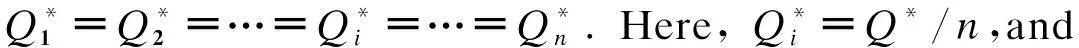
(w-s)F(q2(Q*))-(p-s)F(Q*)+

p-w=0,

(6)

Proof See APPENDIX B.

Inference 1 The optimal total order quantityQ*ofnretailers is a decreasing function on the degree of loss aversionλ, an increasing function on the numbernof retailers, and an increasing function on the delayed payment ratiok′ whens/w≤k′≤1.

Proof See APPENDIX C.

2.2 Decision of the supplier

The supplier is risk neutral and his/her decision is to maximize expected profit. In partial trade credit, the expected profit function of the supplierE[πs(w,k′)] is

Under decentralized decision-making, according to the optimal ordering response function of retailers, the supplier determines the wholesale pricewand the delayed payment ratiok′ to maximize his/her own profit. Then the decision problem of the supplier can be transformed into an optimization problem with the following constraint conditions:

s.t.

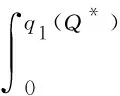
(w-s)F(q2(Q*))-(p-s)F(Q*)+p-w=0.

(7)

It is usually difficult to have an explicit solution for the relationship function amongQ*,k′ andw. So we numerically solve the model (7) to get the optimal total order quantityQ*, the optimal wholesale pricew*, and the optimal delayed payment ratiok′*with the aid of the Lagrange multiplier method.

Thus, we obtain the following equations. The largest expected profit of the supplier is

(w*-c)Q*.

(8)

The largest expected total profit ofnretailers is

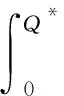
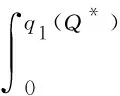
(k′*w*-s)Q*F(q1(Q*)).

(9)

The largest expected total utility ofnretailers is

(10)

3 Numerical Examples

We now employ numerical examples to further analyze and verify the above research. We assume thatp=100,c=40,s=5, and the market demandXis subject to uniform distribution，i.e.,X～U(0, 20 000).

(1) We analyze the influence of the delayed payment ratio on the optimal order decision of the retailers in the case of different degrees of loss aversions and different numbers of retailers, as shown in Fig. 1.

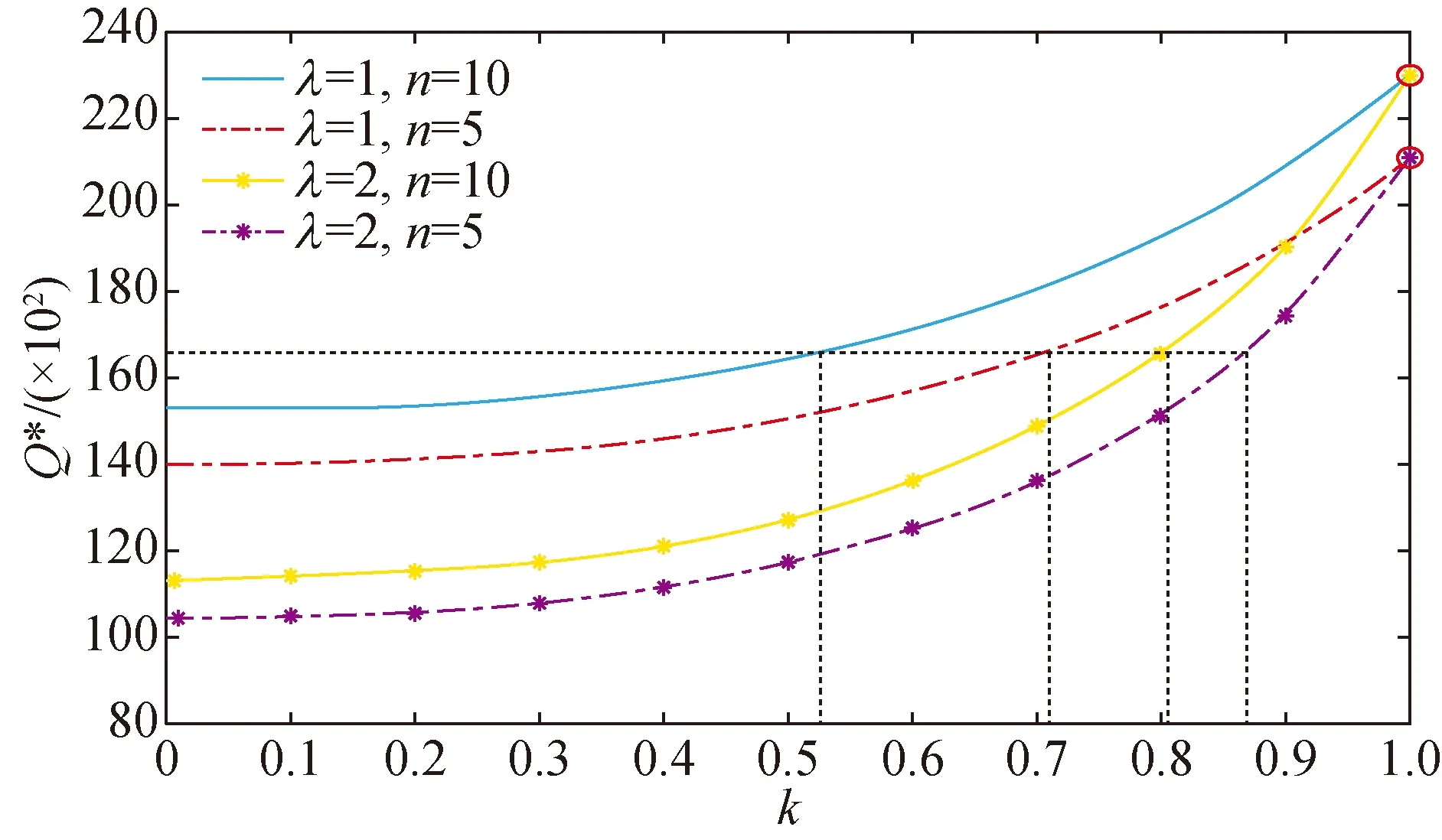
Fig. 1 Influence of delayed payment ratio on the optimal total order quantity of retailers (w=60,1/12≤k′≤1)

As can be seen from Fig. 1, when the degree of loss aversion is the same, in order to make the optimal total order quantity of retailers maintain the same level, the delayed payment ratio offered by the supplier decreases with the increasing number of retailers. When the number of retailers is the same, the proportion of delayed payment offered by the supplier increases rapidly as the loss aversion increases if the optimal total order quantity of retailers is maintained at the same level.

The result is interesting whenk′=1, as seen in Fig. 1. The optimal order quantity will not depend onλwhenk′=1, which can also be justified by Eq. (6) in Theorem 2.

(2) We analyze the influence of the wholesale price on the optimal order decision of the retailers in the case of different degrees of loss aversion and different numbers of retailers, as shown in Fig. 2.

Fig. 2 Influence of wholesale price on the optimal total order quantity of retailers (k′=0.6)

As seen from Fig. 2, the optimal ordering decision of retailers is the decreasing function of the wholesale price inc

4 Conclusions

In this paper, we considered a supply chain where multiple loss-averse retailers can enjoy partial trade credit and purchase items from the supplier to satisfy random demand. We studied the decisions of one-to-multiple supply chains, and obtained the following interesting results about the policy of retailers: (1) Nash equilibrium exists between multiple loss-averse retailers, and a unique optimal total order quantity exists to maximize the expected utility; (2) the optimal total order quantity of retailers is a decreasing function of their loss aversion, an increasing function of the number of retailers, and an increasing function of the proportion of the delayed payment.

In partial trade credit, a delay in payment makes the supplier face a default risk. How will a default risk affect the decision-making policies of the supplier and loss-averse retailers as well as supply chain coordination? This will be our future research. We will also further investigate loss-averse supply chain coordination under partial trade credit considering the following two cases: the supplier is loss averse, and the supplier and retailers are both loss averse.

APPENDIX A

Proof of Theorem 1.

We take the first-order and second-order derivatives ofQifor Eq. (4) and obtain

λ(k′w-s)F(q1(Qi+Q-i))-(λ-1)(w-s)×

F(q2(Qi+Q-i))-(p-s)F(Qi+Q-i)+p-w.

dE[U(πri(Qi,Q-i))]/dQi=0.

Hence, we conclude the proof.

APPENDIX B

Proof of Theorem 2.

From Theorem 1 and its proof process, it can be seen that both the strategy space and the payment function in the ordering game ofnloss-averse retailers meet the requirements of the Nash equilibrium existence theorem, so the game has a pure strategy Nash equilibrium solution. Asnretailers decide the order quantity at the same time in the Nash game, according to the symmetry, the optimal order quantity ofnretailers is equal to that of each other. Then there must beQ1*=Q2*=…=Qi*=…=Qn*.

Obviously,Qi*=Q*/nandQ-i*=(n-1)Q*/n. The two equations are substituted into Eq. (5), which is further simplified, and the equilibrium total order quantity must satisfy Eq. (6).

Let the left side of Eq.(6)be the functionl(Q).

(B1)

Taking the first-order derivative ofQforl(Q), we can obtain the following:

Hence, we conclude the proof.

APPENDIX C

Proof of Inference 1

Based on Eq. (B1), Inference 1 can be proved according to the implicit function derivation rule. The optimal total order quantity ofnretailers decreases with an increase in the degree of loss aversion and increases with an increase in the degree of competition (more retailers mean more competition in the market).

In addition, each retailer determines his/her own order decision based on the wholesale pricewand the delayed payment ratiok′ set by the supplier, and the optimal total order quantityQ*increases with the increase of the delayed payment ratiok′, which indicates that a partial delay in payment strategy plays a part in motivating retailers to a certain extent.

Hence, we conclude the proof.