Wind Speed Prediction by a Hybrid Model Based on Wavelet Transform Technique

LI Shengpeng (李生鹏)， ZHANG Shun (张 顺)， YAO Hongyu (姚洪宇)， CAO Shibao (曹士保)， ZHAO Bing (赵 冰)

State Power Grid Gansu Electric Power Company Electric Power Science Research Institute, Lanzhou 730000, China

Abstract: It is difficult to predict wind speed series accurately due to the instability and randomness of the wind speed series. In order to predict wind speed, authors propose a hybrid model which combines the wavelet transform technique(WTT), the exponential smoothing (ES) method and the back propagation neural network(BPNN), and is termed as WTT-ES-BPNN. Firstly, WTT is applied to the raw wind speed series for removing the useless information. Secondly, the hybrid model integrating the ES method and the BPNN is used to forecast the de-noising data. Finally, the prediction of raw wind speed series is caught. Real data sets of daily mean wind speed in Hebei Province are used to evaluate the forecasting accuracy of the proposed model. Numerical results indicate that the WTT-ES-BPNN is an effective way to improve the accuracy of wind speed prediction.

Key words: wind speed; forecasting; wavelet transform technique(WTT); exponential smoothing(ES) method; back propagation neural network(BPNN)

Introduction

Recently, since global environmental pollution issues have become more and more serious, the production of renewable energy has been drawn much attention to. As one of non-pollution renewable energy, wind has huge potentials for its development. Wind energy is the kinetic energy of the air and mainly depends on wind speed. As a result, it is significant to forecast wind speed accurately in order to improve the reliability of the wind power generation system[1-2].

In the past several years, many scholars proposed a large amount of models on wind speed series forecasting. In general, these methods can be divided into two parts[3]. One is a statistical model, such as the auto regressive integrated moving average (ARIMA) model[4-8], the regression method[9-10], and the exponential smoothing (ES) method[11]. These statistical models have low prediction accuracy. Wind speed series are instability and randomness. However, these models only catch the linear component and neglect the nonlinear component. The other is an artificial intelligence(AI) model, and it is proposed by overcoming the limitation of the statistical model, which is mainly covered by artificial neural networks (ANNs)[12-14]. The AI model has more accurate results in wind speed forecasting than statistical models, and there are a large amount of important applications about daily wind speed forecasting. Zhongetal.[2]employed both an ARIMA and a Kalman filter to build an optimized hybrid model for daily wind speed forecasting in Gansu Corridor. Shukur and Lee[15]proposed a hybrid Kalman filter artificial neural network(KF-ANN) model based on ARIMA forecasting daily wind speed data from Iraq and Malaysia. Guoetal.[16]built a new hybrid daily wind speed prediction model based on the BP neural network and seasonal adjustment, which used a daily mean wind speed series from the year 2001 to 2006 about the Minqin area in Gansu Province, China. Wang and Xiong[17]and Wangetal.[18]proposed a hybrid model consisting of an outlier detection and bivariate fuzzy time series to forecast daily wind speed data sets from January 2008 to December 2012 in Hainan Province, China, and successfully applied support vector regression(SVR) to seasonal index adjustment and Elman recurrent neural network methods analyzed for three different sites in Xinjiang, China. Mohandesetal.[19]built and tested the support vector machine(SVM) model based on daily mean wind speed series from Madina City, Saudi Arabia. Ramasamyetal.[3]used an ANN model to predict daily wind speeds for more than ten locations in the Western Himalayan Indian state of Himachal Pradesh, and temperature, air pressure, solar radiation and altitude were taken as inputs for the ANN model.

The wind speed is affected by comprehensive factors such as topography, climate, temperature and so on, so the wind speed series are unstable and contain noisy. While it will produce large errors when forecasting the series that contain noise directly. Considering the actual characteristics of wind speed series, in this paper, a model named wavelet transform technique exponential smoothing back propagation neural network (WTT-ES-BPNN) for wind speed forecasting is proposed by applying wavelet transform technique(WTT) into a hybrid model which integrates the exponential smoothing and back propagation neural network(BPNN). As we all know, WTT is used to process de-noising in this paper. ES and BPNN capture the linear component and the nonlinear component separately, and then put the prediction values together to get the forecasting values of original data.

The paper is organized as follows: section 1 presents the hybrid model WTT-ES-BPNN for the prediction of wind speed; section 2 provides the evaluation criteria and the numerical results that are compared with other models; section 3 is the conclusions.

1 Proposed Approach

1.1 Wavelet transform and de-noising

WTT is a basic tool for data pre-processing, and its basic idea is the same as the traditional Fourier transform[20]. WTT can be mainly divided into two categories: continuous wavelet transform(CWT) and discrete wavelet transform(DWT).

The expression of CWT is defined as[21]

CWTf(a,b) =〈f(x),ψa, b(x)〉=

(1)

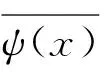
Signalf(x) must be discreted into a discrete series, as well asaandb. Leta=1/2j, andb=i/2j. The expression of DWT is defined as

(2)

wherei,j∈Z.

A one-dimensional signal which contains noisy can be expressed as[22]

s(x)=f(x)+ε×e(x),

(3)

wheref(x) is a real signal,e(x) is a noise signal ands(x) is a signal with noisy. The real signalf(x) often represents low-frequency signal or stable signal.e(x) often represents high-frequency signal. The soft threshold processing method[23]or hard threshold processing method[24]can be used in the process of threshold for the wavelet coefficient.

1.2 Exponential smoothing method

S1=y0,St=αyt-1+(1-α)St-1，t≥2,

(4)

where,αis the smoothing factor and 0<α<1;Stis the smooth value of exponential smoothing at timet;St-1denotes the smoothed value at timet-1;y0is the first data of {yi}.

The value ofαand the initial valueS1are important in ES. However, no formally correct procedure exists for the value choosing. Generally, an appropriate value is also based on the statistician’s judgement[11].

The prediction formula of ES is

1.3 Back propagation neural network

The topological structure about BPNNs has three layers: an input layer, a hidden layer and an output layer. Figure 1 is a typical three layer structure of a BPNN. As shown in Fig. 1,xjis the input value of thejth node in the input layer andj=1, 2, ...,m;wi, jis the weight fromith node in the hidden layer tojth node in the input layer;θirepresents the threshold aboutith node in hidden layer;φis the excitation function in the hidden layer;wk, irepresents the weight fromkth node in the output layer toith node in the hidden layer, andi=1, 2, ...,q;αkrepresents the threshold aboutkth node in the output layer, andk=1, 2, ...,L;ψis the excitation function in the output layer;ykis the output value aboutkth node in the output layer.

Fig. 1 Three layer feed-forward BPNN

In the process of the BPNN, the mainly challenge is how to decide the number of nodes in the hidden layer[25-27], but there is not an uniform approach. In this paper, 2n+ 1 hidden neurons are sufficient to map some functions forninputs, which are based on the Hecht-Nelson method[23], and all weights are assigned with random values initially. The input layer includes five nodes, and each node represents one historical data. The output layer includes one node representing one forecast data.

1.4 Proposed approach

The proposed hybrid model WTT-ES-BPNN for predicting wind speed is a combination of the WTT, the ES and the BPNN. The hybrid model used in this paper is described as follows.

Step 1: The raw wind speed data series are decomposed into two parts, namely the low-frequency component and the high-frequency component by the WTT. The low-frequency component represents the main features of the raw data series, and the high-frequency component is often termed as the noisy signal. The idea of this step is to extract the main characteristics and remove the random disturbance from the raw data series.

Step 2: The ES is used to catch the linear pattern from the low-frequency component of the wind speed series.

Step 3: The BPNN is used to catch the non-linear pattern from the low-frequency component of the wind speed series. The BPNN is constructed from the error between the low-frequency component and the predicted values of the ES.

Step 4: The prediction values of the raw wind speed data series are calculated by adding the predicted values of the residual error series to the predicted values of the ES .

2 Experimental Design and Comparison Results

2.1 Evaluation criteria

In this paper, in order to test the model prediction effect, three forecast error measures are employed as the evaluation criteria: the mean absolute error (MAE), the root mean-square error (RMSE), and the mean absolute percentage error (MAPE).

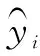
2.2 Data sets and results

In this paper, real data sets of mean daily wind speed in Hebei Province are used to evaluate the forecasting accuracy of the proposed model. The data are collected from October 1, 2013 to September 21, 2014 with a total of 356 values. The mean daily wind speed data from the site are presented in Fig. 2.

It is obvious that the raw data have noise. The WTT is used to remove the noise information from the raw data series. There are many types of wavelet functions. However, in this paper, the wavelet function db2 is applied to remove the noise from the raw data sets and level 1 work best with the series of this paper. Figure 3 shows the low-frequency series and the high-frequency series.

Fig. 2 Mean daily wind speed data

(a)

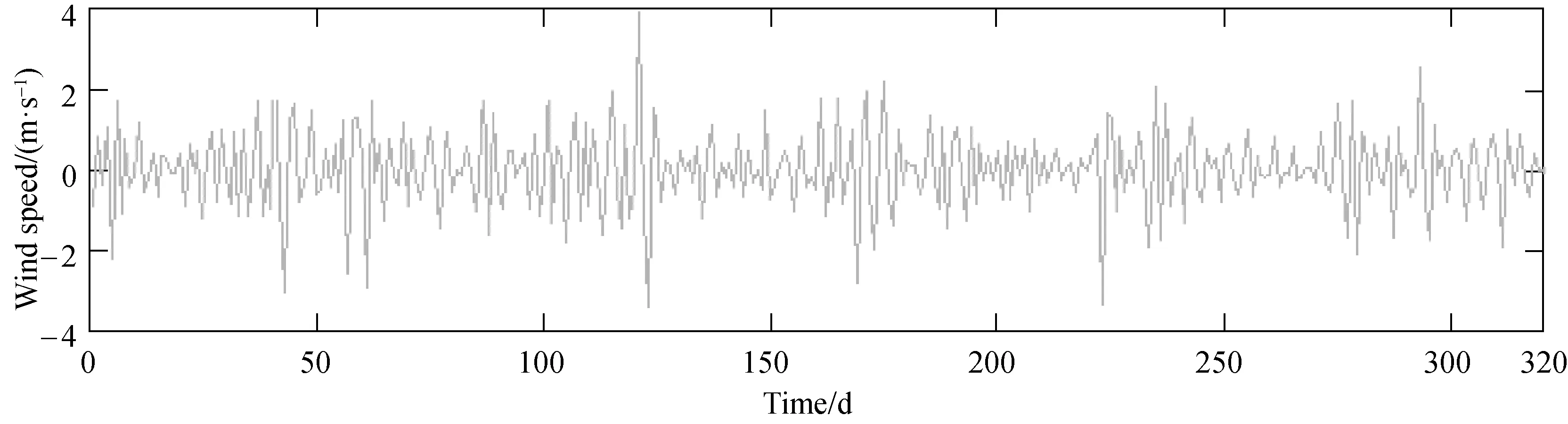
(b)Fig. 3 WTT decomposition process of the raw data: (a) low-frequency component; (b) high-frequency component

Next, the raw wind speed series are predicted. Firstly, the linear component of the low-frequency signals is predicted by the ES. Secondly, the BPNN is used to predict the error between the low-frequency signals and the predicted values of the ES. Finally, the predicted values of the residual error series are added to the predicted values of the ES in order to get the forecasting results of the raw wind speed series.

In the calculation, we use the first 320 data of the low-frequency component as the training sets, while the last 36 data are used to validate the model identified. Figure 4 shows the forecasting results of the raw wind speed.

Fig. 4 Forecasting results of the raw wind speed

2.3 Model comparisons

In order to validate the prediction capacity of the proposed hybrid model, the model comparisons are given in this section. The WTT-ES-BPNN is compared with the BPNN, the ARIMA, the WTT-BPNN, the WTT-ES and the ES-BPNN. The comparison results are shown in Table 1, and the data in Table 1 are obtained by the MATLAB program. It can be clearly seen that the proposed model has the minimum errors of MAE, RMSE and MAPE, which are 0.575 2, 0.763 8 and 0.138 7, respectively. Compared with the hybrid model, the results of the BPNN and the ARIMA present that they have higher values of MAPE(0.327 0 and 0.259 2), which can be indicted that the hybrid model has stronger prediction capacity than the single model. Compared with the hybrid model, the results of the WTT-BPNN and the WTT-ES(0.183 6 and 0.224 9) present that the proposed approach also performs better, which indicates that the WTT-ES-BPNN captures both linearity and non-linearity of the wind speed. When comparing the proposed model with the ES-BPNN, we find wavelet transform and de-noising are reasonable for the daily wind speed series in this study, because the three indices(MAE, RMSE and MAPE) are all greatly improved. As a result, the proposed hybrid model can improve the forecasting performance and it is an effective approach to predict daily wind speed, especially the data in Hebei Province used in this paper.

Table 1 Comparison results among different models

3 Conclusions

Considering instability, randomness and highly-noisy of wind speed, we proposed a hybrid model which combines the WTT, the ES and the BPNN for wind speed forecasting. The main idea of the proposed model is to delete the useless information, and take the linear component and the nonlinear component into consideration. The daily mean wind speed series in Hebei Province are used to evaluate the forecasting accuracy of the proposed model. The WTT-ES-BPNN makes full use of the advantages of single models and numerical results also indicate that the approach is a more effective way to improve the prediction accuracy.

In this paper, we only use the daily wind speed series to prove the proposed hybrid model WTT-ES-BPNN, and realize the one-step prediction by the daily wind speed series in Hebei Province. In the later study, we can also develop a hybrid model for forecasting hourly, monthly, quarterly or even yearly wind speed data, and the multi-step prediction hybrid model will be discussed.