基于模糊PID控制器的麦弗逊悬架联合仿真研究

王孝鹏

（1. 三明学院机电工程学院，福建 三明 365004；2. 机械现代设计制造技术福建省高校工程研究中心，福建 三明 365004；3. 绿色铸锻及其高端零部件制造福建省2011协同创新中心，福建 三明 365004；4. 福建省铸锻零部件工程技术研究中心，福建 三明 365004）

基于模糊PID控制器的麦弗逊悬架联合仿真研究

王孝鹏1, 2, 3, 4

（1. 三明学院机电工程学院，福建 三明 365004；2. 机械现代设计制造技术福建省高校工程研究中心，福建 三明 365004；3. 绿色铸锻及其高端零部件制造福建省2011协同创新中心，福建 三明 365004；4. 福建省铸锻零部件工程技术研究中心，福建 三明 365004）

通过实验测出磁流变阻尼器在不同电流作用下的力与速度关系的阻尼系数特征数据，并将所得阻尼数据导入麦弗逊悬架多体动力学模型；计算簧载质量速度及其变化率作为主动悬架控制的输出量；半主动悬架采用模糊PID复合控制器，用模糊控制策略对PID控制器在给定的参数范围内进行在线实时调整；在MATLAB中搭建悬架系统联合仿真模型。仿真计算结果表明：在各不同车速阶段，采用模糊PID复合控制器均对改善悬架的总体性能有明显作用；且车身垂直加速度、悬架动行程及车轮侧向滑移量在低频阶段改善突出，提升了整车在不同车速范围内的乘坐舒适性与操作稳定性。

磁流变阻尼器；麦弗逊悬架；路面模型；模糊PID；联合仿真

0 引言

车辆在行驶过程中，整车的平顺性与操纵稳定性取决于悬架系统特性的调整。悬架是车身与车轮之间的传力装置，在整车行驶过程中，只有在特定的行驶条件下，被动悬架状态才能达到最优状态，当路面条件或者行驶速度发生变化时，悬架的最优状态会被破坏。因此，对于被动悬架的设计，只能采取折中的方法进行解决。

半主动悬架的核心是采用不同的控制策略对减震器的阻尼特性进行调节。纯模糊控制系统具有不依赖系统的数模模型、鲁棒性好、容错能力强等优点，但是其存在一定的稳态误差。经典的PID控制策略可以较好地消除系统的稳态误差，采用模糊PID复合控制策略，可以把两种控制器的优势结合起来，实现优势互补，获得较好的控制效果。半主动悬架是近些年相关文献研究的一个热点。相对于主动悬架，半主动悬架主要通过改变减震器的可变力输出来控制整车的震动特性，其性能与主动悬架接近。相比于主动悬架，半主动悬架的结构转较为简单，能耗较小[1-8]。因此，本文拟通过建立麦弗逊主动悬架联合仿真模型，采用模糊PID控制器对1/4整车模型进行仿真研究，并且与被动悬架的性能进行对比，分析悬架在各个不同车速段的车速加速度、悬架动行程以及车轮侧向滑移量等的特性，以期为车辆的稳定性设计提供一定的理论参考依据。

1 麦弗逊模型

麦弗逊悬架多体动力模型的建立是联合仿真的前提工作，其建模精度将直接导致仿真结果与真实实验的差距。

1.1 磁流变阻尼器实验

具有良好可调性能的磁流变阻尼器是半主动悬架系统的关键设备之一。磁流变液是一种在磁场控制下黏性会发生明显变化的特殊磁性流体，在一定的磁场强度下，流体会停止流动达到固化；而当去掉外加磁场时，流体又会恢复到原来的流体状态。这种效应实现了磁流变液在液态和固态之间的转换，且这种转换是可逆的，因此具有较大的工程应用价值。

本实验在西安交通大学振动与噪声控制研究所振动室内进行，试验台如图1所示。实验过程中，位移传感器安装在低频振动实验台内，压力传感器的一端通过螺杆固定在振动台支架上，而另一端通过套管连接至磁流变阻尼器的活塞杆，磁流变阻尼器的线圈导线经中空活塞杆后通过套管引出。

图1 磁流变阻尼器试验台Fig. 1 Magneto-rheological damper test rig

具体的实验方法如下：实验中，将磁流变阻尼器垂直安装，一端固定在台架上，另一端由配备了电测系统和计算机控制系统的低频振动台实现简谐运动。实验室内的温度保持在常温状态；实验行程变化范围为0.01～0.04 m；速度变化范围为0.063（0.02π）～ 0.380（0.12π）m/s。磁流变阻尼器的初始位置大致在阻尼器行程的中间。实验中，使用的磁流变液为重庆仪表材料研究所生产的MRF-01K型磁流变液，其密度为2.65 g/cm3；零场黏度（=14 s-1，20 ℃）为0.6 Pa·s；工作温度范围为-20～100 ℃。图2所示为垂向振幅a=0.02 m，频率f=2 Hz，输入电流I=0, 1, 2, 3 A时的阻尼力与速度关系图。

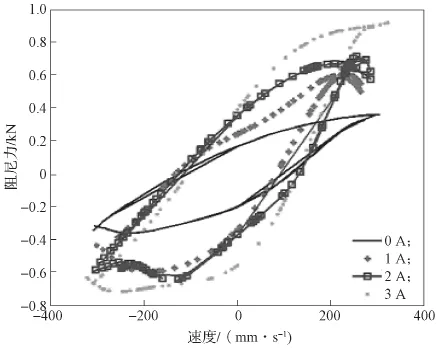
图2 阻尼系数特性图Fig. 2 Damping coef fi cient characteristic diagram

由图2 可知：在输入电流不同的情况下，磁流变阻尼器的阻尼性能发生了变化。输入电流为0 A时，由于此时没有剪切力，因此测得的只是黏滞力和摩擦力之和。随着输入电流的增加，磁滞区剪切力出现并不断增大，总阻尼力也不断增加。

1.2 悬架模型

大多数基于联合仿真的文献在模型建立中存在如下问题：

1）采用弹簧质量系统模拟悬架运动特征，此模型能较好地反映悬架的垂直震动特性，但是不能反映悬架的实际运行状态，并且忽略了车轮的侧性运动。

2）悬架的下控制臂与转向横拉杆与地面进行相互约束，弹簧减震器直接与车身或地面直接连接；正确应为与车身进行约束，在车身与弹簧减震器之间添加无质量的虚部件。

此模型虽然具有悬架模型的多体形式，且能反映悬架的K&C特性，但是车身与车轮之间相对（悬架动行程）与真实情况不相符。因此，本文拟通过ADAMS软件建立麦弗逊悬架模型，在减震器上下安装点分别建立安装部件，下安装点部件的虚部件与转向节点固定连接，上安装点部件与车身的胡克副连接，上安装点部件与下安装点部件的圆柱副连接，转向横拉杆与下控制臂与车身分别为球副与旋转副连接。同时，在减震器上下安装点之间建立主动力函数，在测试试验台建立路面输入函数，模拟B级路面不同车速段的输入；将实验测得的磁流变液阻尼器特性曲线输入麦弗逊悬架中，建立好的麦弗逊悬架模型主视与侧视图如图3所示。

图3 麦弗逊主动悬架模型Fig. 3 Macppherson active suspension model

建立车身的速度、加速度、悬架动行程及车轮侧向滑移量状态输出函数如下：

VY(.adams_view_zhengche.body.cm)；

ACCY(.adams_view_zhengche.body.cm)；

DZ(MARKER_76, test_patch.cm)+0.367 4；

DY(body.cm, wheel_right.cm)-DY(body_cm, ground.wheel_cm)+11.4。

建立的悬架主动力、路面状态输入函数如下：

VARVAL(.adams_view_zhengche.zhudongli_ shuru)；

VARVAL(.adams_view_zhengche.road_shuru)。

2 路面模型

对悬架性能分析时，需要输入路面模型。根据国家标准将公路等级分为8种，在不同的路段测量，很难得到两个完全相同的路面轮廓曲线。通常是将测量得到的大量路面不平度随机数据经数据处理后得到路面的功率谱密度。产生随机路面不平度时间轮廓有两种方法，即由白噪声通过一个积分器产生或者由白噪声通过一个成型滤波器产生。

路面时域模型可用公式（1）描述：

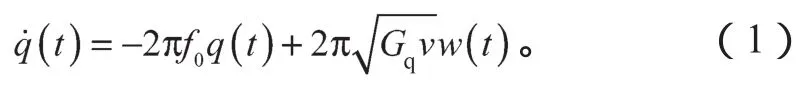
式中：f0为时间频率；

q(t)为路面随激励；

Gq为路面不平度系数；

v为汽车行驶速度；

w(t)为积分白噪声。

根据公式（1）建立B级路面不同车速的仿真模型，如图4所示。B级路面不同车速的垂直位移计算结果如图5所示。由图5可知：随着车速的增加，路面谱的垂向位移成比例缩放，路面谱随时间变化的趋势相一致。

图4 B级路面不同车速Gain 6时域仿真模型Fig. 4 Time domain simulation model of class B road under different speeds

图5 B级路面各车速垂向位移Fig. 5 Vertical displacementon class B road under different speeds

3 模糊PID控制器设计

模糊PID复合控制器具有PID与模糊控制器各自的优势。其中PID控制具有调节原理简单、参数容易整定和实用性较强等优点，其控制规律如公式（2）所示：

式中：u(t)为实时主动控制力；

Kp为比例系数；

e(t)为实时误差，即车身速度与理想值间差值；

Ki为时间极品常数；

Kd为微分时间常数。

模糊PID控制系统的输入，为车身的速度及其变化量，其输出为主控制力；模糊控制器的输出为ΔKp, ΔKi, ΔKd，实际的PID控制参数如公式（3）～（5）描述：

式中：Kp、Ki、Kd为预设PID控制参数；

Hp、Hi、Hd为比例因子。

模糊控制规则是模糊控制器的核心，它用语言的方式描述了控制器输入量与输出量之间的关系。悬架的输入输出分别采用7个语言变量规则进行描述：负大（-3）、负中（-2）、负小（-1）、零（0）、正小（1）、正中（2）、正大（3）。输入采用高斯隶属函数，以保证输入参数的平缓且稳定性好；输出采用三角隶属函数，以保证其较好的灵敏度。当误差较大时，Kp取较大值，系统响应较快，模糊控制系统输出较大的ΔKp值，ΔKd取较小值，避免系统出现过大超调量线性，产生不稳定现象；当误差中等时，Kp取较中间值，保证系统具有较小的超调量，ΔKd取值不变或者稍微减小，Ki取适当值；当误差较小时，Kp取较小值；当误差及其变化率方向一致时，说明误差有增大的趋势，此时应取较大的ΔKp值[8-12]。误差及其变化率同ΔKp、ΔKi、ΔKd的模糊控制规则如表1～表3所示。根据式（2）～（5）及模糊控制规则，建立模糊PID复合控制器，如图6所示。

表1 模糊控制规则ΔKpTable 1 Fuzzy control rules of ΔKp

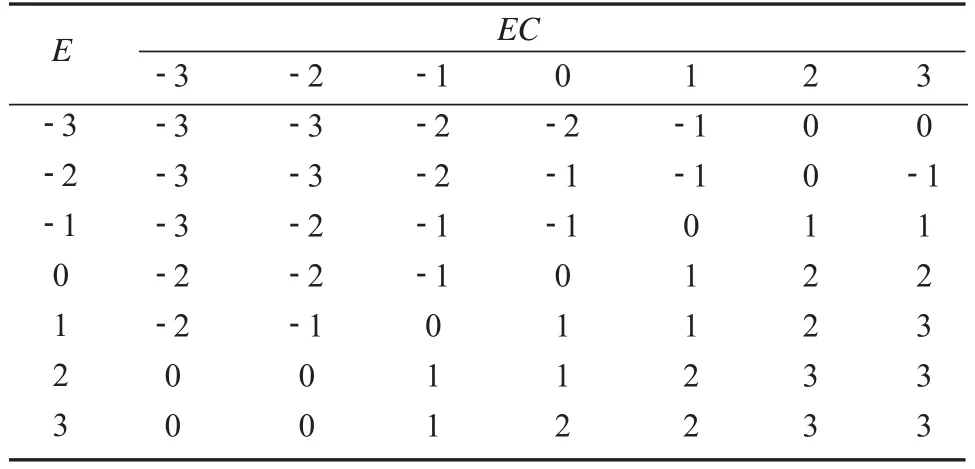
表2 模糊控制规则ΔKiTable 2 Fuzzy control rules of ΔKi

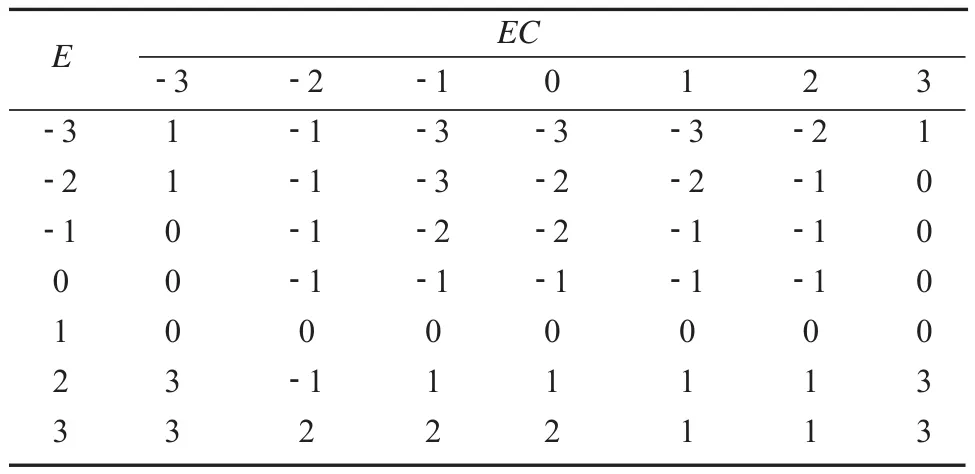
表3 模糊控制规则ΔKdTable 3 Fuzzy control rules of ΔKd

图6 模糊PID控制器Fig. 6 Fuzzy PID controller

4 仿真分析

导通ADAMS与MATLAB软件之间通信，其状态函数见图7；对路面及模糊PID复合控制器进行封装，建立ADAMS主动悬架联合仿真模型，见图8。

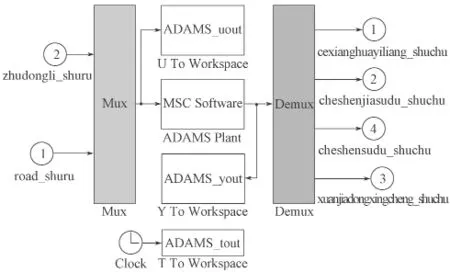
图7 通信状态函数Fig. 7 Communication status function

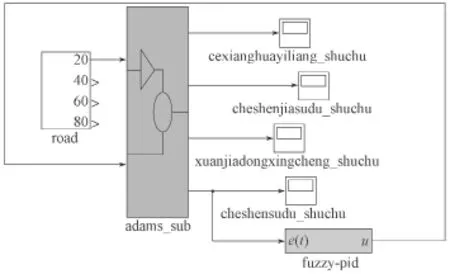
图8 联合仿真模型Fig. 8 Co-simulation model

在B级路面上，车辆分别以20, 40, 60, 80 km/h的速度直线行驶，计算主被动悬架的车身加速度、悬架动行程、车轮侧向滑移量，所得计算结果见图9～11，仿真步长为0.005 s，仿真时间为10 s。

从图9～11所示计算结果变化曲线可以看出，主动悬架相对于被动悬架，在性能上整体都有所提升。在各不同车速阶段，车身垂直加速度、悬架动行程、轮胎动位移性能均有所改善。其中，车身垂向加速度的改善尤为突出，在全速范围内改善了车辆行驶的乘坐舒适性。随着车速的增加，悬架动行程及侧向滑移量少有改善，增加了整车行驶过程中的操作稳定性。各个速度段的悬架性能参数变化如表4所示。

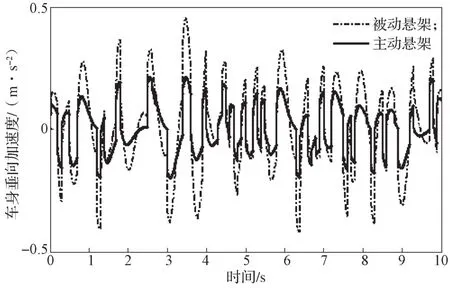
图9 车身垂向加速度变化曲线Fig. 9 Body vertical acceleration

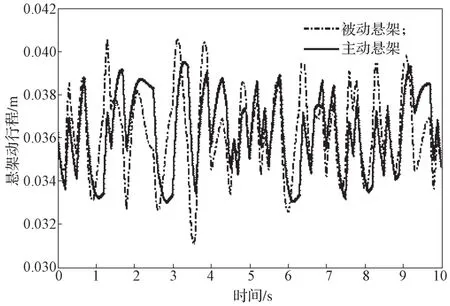
图10 悬挂动行程变化曲线Fig. 10 Suspension dynamic travel

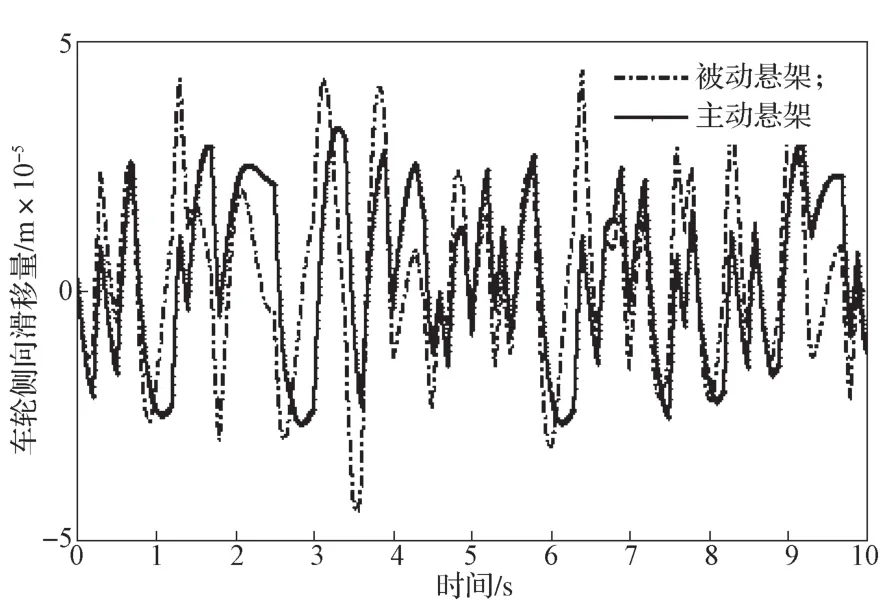
图11 车轮侧向滑移量变化曲线Fig. 11 Curves of wheel lateral slip

表4 主被动悬架性能参数值Table 4 Performance parameter value of main passive suspension

图12和13分别为车身加速度、悬架动行程的功率谱曲线。从图12和13所示功率谱变化曲线中可以得知，整车运行过程中，主动悬架的幅值相对被动悬架的都较小。同时可以得知，振幅最大值都出现在频率较小处，即低频路面输入信息对整车的震动特性较大，悬架动行程在高频路面激励下车轮的震动得到了较好的抑制。

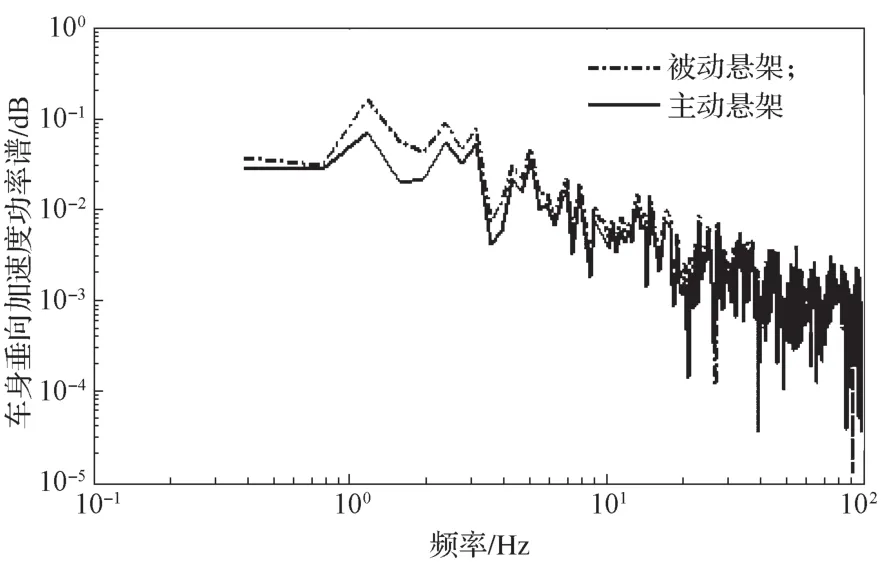
图12 车身加速度功率谱变化曲线Fig. 12 Power spectrum of vehicle acceleration

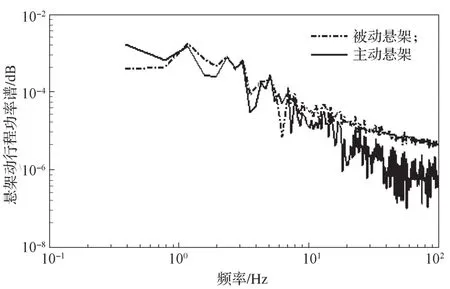
图13 悬挂动行程的功率谱变化曲线Fig. 13 Power spectrum of suspension displacement

5 结论

本文通过建立麦弗逊主动悬架联合仿真模型，采用模糊PID复合控制器对阻尼力进行控制，分析悬架在各个不同车速段的车身垂直加速度、悬架动行程及车轮侧向滑移量特性，可得出如下结论：

1）车身的垂直加速度、悬架动行程及车轮侧向滑移量在全速范围内均有改善，且车身垂直加速度提升尤为明显，提升了整车乘坐舒适性与操作稳定性；

2）车身的垂直加速度、悬架动行程功率谱幅值，在全频段相对被动悬架幅值都较小；低频状态时对悬架性能的影响显著；

3）模糊PID控制器整的体综合性能优越，鲁棒性强，满足对整车全速范围内实时最优参数控制。

[1] 杨礼康. 基于磁流变技术的车辆半主动悬挂系统理论与试验研究[D]. 杭州：浙江大学，2003. YANG Likang. An Theoret1ea1 and Experimental Investigation on Semi-Aet1ve Vehicle Suspens1on Emp1oying Magneto-Rheologieal Teehnology[D]. Hangzhou：Zhejiang University，2003.

[2] 唐志桥. 二分之一车辆悬架系统的动力学仿真研究[J].公路与汽运，2015 (1) ：5-8，56. TANG Zhiqiao. Dynamic Simulation of Half Vehicle Suspension System[J]. Highways & Automotive Applications，2015 (1) ：5-8，56.

[3] 刘 静. 带天棚阻尼的1/2车辆主动悬架仿真研究[J].公路与汽运，2015，166 (3) ：15-20，80. LIU Jing. The Skyhook Active Suspension Simulation Research of Half Vehicles[J]. Highways & Automotive Applications，2015，166(3) ：15-20，80.

[4] 张 洁. 公路车辆与桥梁耦合振动分析研究[D]. 成都：西南交通大学，2007. ZHANG Jie. Studies on Coupling Vibration of Highway Vehicle-Bridge System[D]. Chengdu：Southwest Jiaotong University，2007.

[5] XU X，ZHOU K K，ZOU N N，et al. Hierarchical Control of Ride Height System for Electronically Controlled Air Suspension Based on Variable Structure and Fuzzy Control Theory[J]. Chinese Journal of Mechanical Engineering，2015，28(5) ：945-953.

[6] 喻 凡，林 逸. 汽车系统动力学[M]. 北京：机械工业出版社，2012：171-172. YU Fan，LIN Yi. Automotive Systems Dynamics[M]. Beijing：Machinery Industry Press，2012：171-172.

[7] 周 兵，赵保华. 汽车主动悬架自适应模糊PID控制仿真研究[J]. 湖南大学学报（自然科学版），2009，36(12) ：27-30. ZHOU Bing，ZHAO Baohua.Simulation Study of Self-Adaptive Fuzzy-PID Control of Active Suspension[J]. Journal of Hunan University(Natural Sciences)，2009，36(12) ：27-30.

[8] 张 昆，习文辉，邓文华，等. 基于CarSim-Simulink联合仿真的整车半主动悬架模糊控制仿真研究[J]. 昆明理工大学学报（自然科学版），2015，40(1) ：39-44. ZHANG Kun，XI Wenhui，DENG Wenhua，et al. Fuzzy Control Simulation of Full Vehicle Semi-Active Suspension Based on Carsim-Simulink Co-Simulation[J]. Journal of Kunming University of Science and Technology（Natural Science Edition），2015，40(1) ：39-44.

[9] SU Xiaojie，YANG Xiaozhan，SHI Peng，et al. Fuzzy Control of Nonlinear Electromagnetic Suspension Systems[J]. Mechatronics，2014，24(4) ：328-335.

[10] LI R，CHEN W M，LIAO C R，et al. Fuzzy Hybrid Control of Vibration Attitude of Full Carvia Magneto-Rheological Suspensions[J]. Chinese Journal of Mechanical Engineering，2010，23(1) ：72-79.

[11] NGUYEN S D, CHOI S B. A Novel Minimum- Maximum Data-Clustering Algorithm for Vibration Control of a Semi-Active Vehicle Suspension System[J]. Noise & Vibration Bulletin，2013，227(9) ：1242-1254.

[12] GUANJ F，GU L，HOU C Z，et al. Fuzzy Logic Control for Semi-Active Suspension System of Tracked Vehicle[J]. Journal of Beijing Institute of Technology，2004，13(2) ：113-117.

（责任编辑：廖友媛）

A Co-Simulation Research on Macpherson Suspensions Based on Fuzzy-PID Controllers

WANG Xiaopeng1,2,3,4
（1. School of Mechanical & Electronic Engineering, Sanming University，Sanming Fujian 365004，China；2. Engineering Research Center in Fujian Province University for Modern Mechanical Design and Manufacturing Technology，Sanming Fujian 365004，China；3. Fujian Provincial Collaborative Innovation Center for Green Casting，Forging and Advanced Manufacturing，Sanming Fujian 365004，China；4. Fujian Provincial Engineering Research Center for Castingand Forging Parts，Sanming Fujian 365004，China）

The characteristic data of damping coefficient of the magneto-rheological damper, which are concerning the relationship between force and velocity, are to be measured under different currents and to be introduced to the multi-body dynamic simulation model of Macpherson suspension. With the sprung mass velocity and its change rate as the active suspension control output, the semi-active suspension adopts the fuzzy PID controller, followed by an online real time adjustment of fuzzy PID controller with a fuzzy control strategy within a given parameter range, thus establishing a co-simulation model of the suspension system in MATLAB. The simulation results show that: at different speed stages, the fuzzy PID controller has an obvious effect on the improvement of the overall performance of the suspension.The vertical acceleration of the vehicle body, the dynamic stroke of the suspension and the lateral slip of the wheel are drastically improved at the low frequency stage, and the ride comfort and handing stability of the vehicle are enhanced in different speed ranges.

magneto-rheological damper (MRF damper)；Macpherson suspension；road model；fuzzy PID；co-simulation

U270.1

A

1673-9833(2017)02-0066-06

10.3969/j.issn.1673-9833.2017.02.012

2016-11-26

福建省省属高校科研专项基金资助项目（JK2014048）

王孝鹏（1983-），男，山西运城人，三明学院讲师，硕士，主要研究方向为车辆系统动力学及控制，汽车NVH分析与控制，E-mail：mrxp1984@163.com