短肢剪力墙结构扭转效应有限元分析

周 磊，杨晓华，卢学臣

（湖南工业大学 土木工程学院，湖南 株洲 412007）

短肢剪力墙结构扭转效应有限元分析

周 磊，杨晓华，卢学臣

（湖南工业大学 土木工程学院，湖南 株洲 412007）

利用ANSYS有限元分析软件，建立三层短肢剪力墙空间结构有限元模型，通过改变控制参数和受力条件，研究轴压比、荷载偏心距和节点区箍筋配筋率对短肢剪力墙结构抗扭承载能力的影响，并将计算结果与一个结构模型试验结果进行对比。计算结果表明：当轴压比小于等于0.5时，短肢剪力墙结构抗扭承载能力随轴压比增加而增大，当轴压比超过0.5以后，结构抗扭承载能力随轴压比增加而降低；荷载偏心距增大，扭转效应加强，结构承载能力降低，扭矩增加加速了连梁端部受拉破坏，外边缘结构的连梁端部受到弯剪扭复合作用，是结构抗震的薄弱位置，建议加强配筋；适当增加节点区水平箍筋配筋率能有效提高结构抗扭承载能力。

短肢剪力墙空间结构；扭转效应；轴压比；偏心距；节点区箍筋配筋率

0 引言

短肢剪力墙结构是一种介于异形柱和剪力墙之间的结构形式，具有结构布置灵活、节能等优点，被广泛应用于民用住宅、宾馆客房等建筑中，因此，研究其抗震性能具有重要意义。结构的地震反应是多维的[1]，由此而引起的结构扭转效应是造成结构破坏的一个重要原因[2]。在短肢剪力墙结构抗震性能方面，对单个墙肢构件或对单个节点构件的研究较多[3-9]，而利用三维空间结构模型对在水平地震荷载作用下结构节点抗扭转的研究较少[10-11]，由此得出的相关结论并不能完全说明短肢剪力墙节点扭转的破坏机理。

本文建立一个三层短肢剪力墙空间结构有限元模型，对受扭转作用下的短肢剪力墙空间结构的墙肢节点进行研究，通过改变控制参数和受力条件，研究轴压比、荷载偏心距、节点区箍筋配筋率对短肢剪力墙结构抗扭承载能力的影响。

1 模型建立

1.1 结构原型

为便于同结构试验结果进行对比，本文建立的有限元分析模型完全参照一个典型结构试验模型，该试验模型是按实际工程结构设计的1/4缩尺比例的两跨三层短肢剪力墙空间结构模型，短肢剪力墙肢厚比为5。结构模型基本尺寸如图1所示，单位为mm。

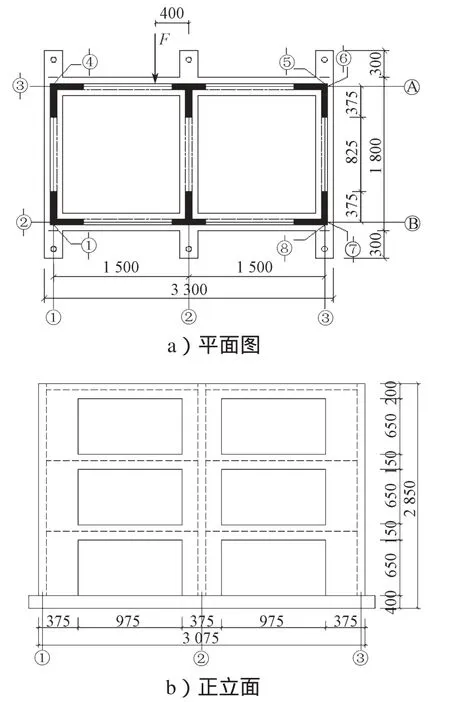
图1 结构试验模型Fig. 1 Test model of structures

1.2 有限元分析模型

采用ANSYS有限元软件建立短肢剪力墙结构分析模型，并对结构进行非线性有限元分析。考虑到短肢剪力墙中钢筋较多，且分布比较均匀的特点，本文采用整体式方式建立有限元分析模型，划分单元采用含筋的SOLID65混凝土分析单元，认为钢筋以均匀分布的形式含在混凝土中。

结构非线性分析中混凝土本构关系采用多线性等向强化模型。根据GB50010—2010《混凝土结构设计规范》[12]规定的混凝土单轴应力-应变关系公式，用一系列数据点拟合混凝土的本构关系，混凝土材料特性为：抗压强度设计值fc=11.9 N/mm2，抗拉强度设计值ft=1.27 N/mm2，泊松比v=0.2。采用双线性等向强化模型模拟钢筋的本构关系，钢筋材料特性为：弹性模量E=2×105MPa，抗拉强度设计值fy=300 N/mm2，泊松比v=0.3。为保证结构非线性分析中结果收敛，关闭了含钢筋SOLID65混凝土分析单元压碎开关，通过设置剪力传递系数来考虑混凝土出现裂缝时的剪切力损失。整体模型采用六面体映射划分，建立的有限元分析模型如图2所示。

图2 有限元模型Fig. 2 A fi nite element model

1.3 边界条件的确定

根据结构试验模型的具体试验情况和实际工程工作状态，对建立的有限元分析模型底部所有节点施加固定端约束，即限制有限元分析模型底部所有单元节点沿3个坐标轴方向上的位移为0 mm，在顶层距中轴线400 mm处施加循环往复的水平集中荷载。

利用建立的有限元分析模型，通过改变不同的控制参数来作如下研究：

1）根据工程实际受力情况，在顶层屋面施加一组固定不变的竖向面荷载，然后对顶层连梁单元不同节点施加循环往复的水平集中荷载。由于施加水平荷载的节点不同，荷载偏心距发生改变，对整体结构施加的扭矩也发生改变，以此来研究扭矩大小对短肢剪力墙整体结构受力性能的影响。

2）施加单一偏心循环往复荷载，根据不同的轴压比对顶层屋面施加不同的竖向均布压力，以此研究不同轴压比对短肢剪力墙结构抗扭承载力的影响。

3）根据工程实际受力情况，在顶层屋面施加一组固定不变的竖向面荷载，然后对顶层连梁单元固定节点施加循环往复的水平集中荷载，再改变短肢剪力墙和连梁节点区域水平箍筋配筋率，研究不同箍筋配筋率对结构扭转抗震性能的影响。

2 结果分析

2.1 有限元分析结果与试验结果的比较

在有限元分析模型的顶层连梁上施加单调逐级增加的偏心循环往复水平集中荷载，集中荷载施加点偏中间对称轴400 mm。计算得到顶层平面左上角点处水平侧移和左右上角点水平位移差与施加外力的关系曲线，并将计算结果与已经完成的结构模型试验结果进行比较，比较结果如图3和图4所示。

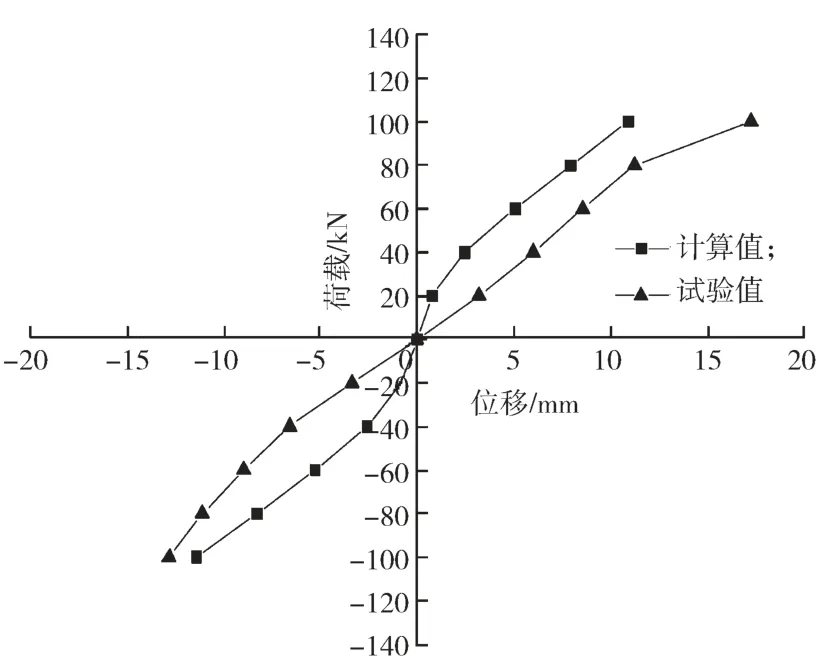
图3 左上角点水平位移曲线Fig. 3 Horizontal displacement curves

图4 左右上角点水平位移差值曲线Fig. 4 Horizontal displacement difference curves

由图3和图4可知，有限元计算分析结果与结构模型试验结果变化趋势一致。在加载中前期，计算值与试验值比较接近，结果吻合程度较高，这说明建立的有限元分析模型可以较好地模拟短肢剪力墙结构的水平抗扭性能的分析。由于建立的有限元分析模型是理想均匀模型，没有考虑实际结构中材料物理性质的差异，所以在同样的水平外力作用下，结构模型试验测量到的位移值大于有限元分析模型的计算值。

2.2 轴压比对抗震性能的影响

轴压比[12-13]大小是影响短肢剪力墙结构抗震性能的重要因素之一。针对所建立的有限元结构分析模型，在各层楼面板和屋面板上施加不同的面荷载。这些面荷载最终传递到短肢剪力墙上，再根据短肢剪力墙承受的竖向荷载和横截面积换算成轴压比。然后在有限元结构模型的顶层楼盖对应节点上施加偏心距为400 mm的循环往复水平集中荷载，外荷载逐级加入，每级增加20 kN，直到有限元计算网格发生破坏而中止。计算得到的最大水平循环外荷载与短肢剪力墙轴压比之间的关系如图5所示。

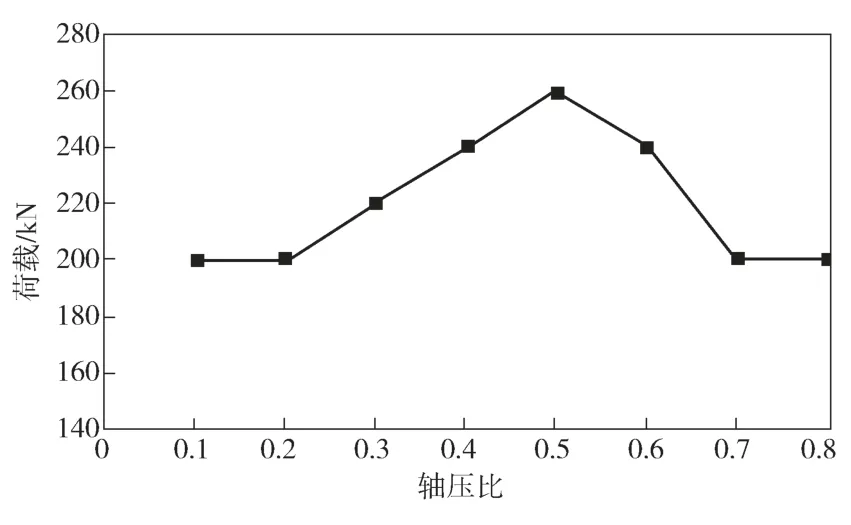
图5 不同轴压比下的结构极限荷载Fig. 5 Ultimate load of structure under different axial compression ratios

由图5可知，结构的抗扭承载能力随着轴压比的递增呈现先增加后减小的变化趋势。当轴压比不超过0.5时，轴压比的增加可以有效地提高结构的极限承载能力；当轴压比大于0.5以后，轴压比的增加对结构抗震反而不利，结构的抗扭承载能力随之减小。

图6给出了具有不同轴压比的有限元结构分析模型的顶层平面角点在200 kN循环往复水平荷载作用下的最大水平位移。

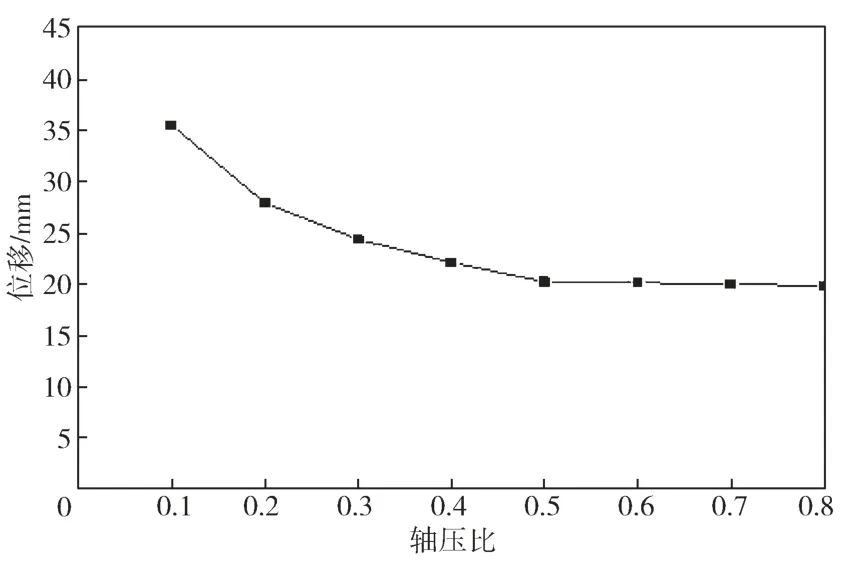
图6 不同轴压比时结构顶层角点水平位移Fig. 6 Ultimate displacement of structure under different axial compression ratios

由图6可知，同等荷载条件下，轴压比增大，结构侧移减小，延性减弱，轴压比增加可以缩小短肢剪力墙结构水平方向上的变形。结合图5和图6可以得出，JGJ3—2010《高层建筑混凝土结构技术规程》[13]给出的短肢剪力墙轴压比限值为0.45是比较合理的。

2.3 偏心距对抗震性能的影响

在轴压比为0.3，偏心距分别为400, 750, 1 100, 1 500 mm时，对模型进行数值模拟，研究扭矩对结构的破坏情况及其承载力的影响，模拟结果如表1所示。

表1 偏心距对结构受力性能的影响Table 1 In fl uence of eccentricity on the structure performance

从表1可以看出，结构破坏情况都表现为①轴线位置连梁端部单元破坏。偏心距增大，扭转效应加强，结构承载能力降低，扭矩的增加使得连梁端部受拉破坏加速，结构未能充分发挥承载能力。外边缘结构的连梁端部受到弯剪扭复合作用，是结构抗震的薄弱位置，建议加强配筋。

2.4 节点区箍筋配筋率对抗震性能的影响

JGJ149—2006《混凝土异形柱结构技术规程》[14]中，对异形柱节点核心区水平箍筋的间距和配筋率作了限定。本文针对建立的有限元分析模型，通过改变节点区域箍筋间距来调整配筋率，研究节点区域箍筋配筋率对短肢剪力墙结构水平抗扭承载能力的影响，设定轴压比为0.3，计算结果如表2所示。

表2 节点区箍筋配筋率对结构承载能力的影响Table 2 In fl uence of node-area stirrup reinforcement ratio on the structure’s bearing capacity

从表2中可以看出，当节点区水平箍筋配筋率从0.37%提高至0.48%时，其承载力提高约9%，后期继续增加配筋率，承载力不再提高。因此，在低配箍率时适当提高短肢剪力墙结构节点核心区箍筋配筋率，对提高结构抗震性能是有利的。

3 结论

ANSYS有限元分析，可以较好地模拟偏心水平循环荷载作用下，短肢剪力墙结构的受力情况，通过前面的研究，可得出如下结论。

结构的抗扭承载能力随着轴压比的递增呈现先增加后减小的变化趋势，当轴压比小于等于0.5时，轴压比的增加可以有效地提高结构的极限承载能力。

偏心距增大,结构承载能力降低,扭矩的增加使得连梁端部受拉破坏加速,外边缘结构的连梁端部受到弯剪扭复合作用，是结构抗震的薄弱位置，建议加强配筋。

在低配箍率时，适当增加节点区水平箍筋配筋率能提高结构抗扭承载能力。当节点区水平箍筋配筋率达到一定值后，再提高节点区水平箍筋配筋率，其水平抗扭承载力不再提高。

[1] 李宏男. 结构多维抗震理论与设计方法[M]. 北京：科学出版社，1998：53. LI Hongnan. Multidimensional Aaseismic Theory and Design Methods[M]. Beijing：Science Press，1998：53.

[2] 徐培福，黄吉峰，韦承基. 高层建筑结构的扭转反应控制[J]. 土木工程学报，2006，39(7)：1-8. XU Peifu，HUANG Jifeng，WEI Chengji. Control of Torsional Response of Tall Building Structures[J]. China Civil Engineering Journal，2006，39(7)：1-8.

[3] 傅剑平. 钢筋混凝土框架节点抗震性能与设计方法研究[D]. 重庆：重庆大学，2002. FU Jianping. Seismic Behavior and Design of Joints in a Reinforced Concrete Frame[D]. Chongqing：Chongqing University：2002.

[4] 黄东升，程文瀼，彭 飞. 对称双肢短肢剪力墙的低周反复荷载试验研究[J]. 建筑结构学报，2005，26(3)：51-56. HUANG Dongsheng，CHENG Wenrang，PENG Fei. Low-Cycle Loading Experiment Study on Symmetric Double Short-Pier Shear Walls[J]. Journal of Building Structure，2005，26(3)：51-56.

[5] 彭 飞，程文瀼，陆和燕. 对称双肢短肢剪力墙的拟静力试验研究[J]. 建筑结构学报，2008，29(1)：64-69. PENG Fei，CHENG Wenrang，LU Heyan. Quasi-Static Test Research of Symmetric Double Short-Limb Shear Walls[J]. Journal of Building Structure，2008，29(1)：64-69.

[6] 都洪钢. T形截面短肢剪力墙中间层中节点抗震性能试验研究[D]. 重庆：重庆大学，2006. DU Honggang. Experimental Research on the Seismic Behavior of Interior Joints of T Shaped Short Pier Shear Wall[D]. Chongqing：Chongqing University，2006.

[7] 况建刚. T型短肢剪力墙中间层端节点抗震性能试验研究[D]. 重庆：重庆大学，2006. KUANG Jiangang. Experimental Research on Seismic Behavior of Exterior Joints of T-Shape Short Pier Shear Wall[D]. Chongqing：Chongqing University，2006.

[8] 王 飞. 短肢墙预应力楼盖结构顶层端节点抗震性能试验研究[D]. 重庆：重庆大学，2004. WANG Fei. The Earthquake-Resistant Experimental Researches on Top Story Knee Joint of Concrete Structures with Short Shear Wall and Unbonded Tendons Prestressed Floor[D]. Chongqing：Chongqing University，2004.

[9] 冯建平，吴修文. T形截面柱框架边节点的抗震性能[J].华南理工大学学报（自然科学版），1995，23(3)：123-130. FENG Jianping，WU Xiuwen. Seismic Behavior of Exterior Beam-T Column Joints[J]. Journal of South China University of Technology(Natural Science) ，1995，23(3)：123-130.

[10] 程绍革，陈善阳，刘经纬. 高层建筑短肢剪力墙结构振动台试验研究[J]. 建筑科学，2000，16(1)：12-16. CHENG Shaoge，CHEN Shanyang，LIU Jingwei. A Shaking Table Test on Shear Wall Structure with Framed Short Pillars for High-Rise Buildings[J]. Building Science，2000，16(1)：12-16.

[11] 张 晋，吕志涛. 短肢剪力墙-筒体结构模型振动台试验研究[J]. 东南大学学报（自然科学版），2001，31(6)：4-8. ZHANG Jing，LZhitao. Earthquake Simulation Test of Short-Leg Shear Wall-Tube Model[J]. Journal of Southeast University(Natural Science Edition)，2001，31(6)：4-8.

[12] 中华人民共和国住房和城乡建设部.混凝土结构设计规范：GB 50010—2010[S]. 北京：中国建筑工业出版社，2010：35. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Design of Concrete Structures：GB 50010—2010[S]. Beijing：China Building Industry Press，2010：35.

[13] 中华人民共和国住房和城乡建设部. 高层建筑混凝土结构技术规程：JGJ 3—2010[S]. 北京：中国建筑工业出版社，2010：80. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Technical Speci fi cation for Concrete Structures of Tall Buildings：JGJ 3—2010[S]. Beijing：China Building Industry Press，2010：80

[14] 中华人民共和国住房和城乡建设部. 混凝土异形柱结构技术规程：JGJ 149—2006[S]. 北京：中国建筑工业出版社，2006：36. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Technical Speci fi cation for Concrete Structure with Special-Shaped Columns：JGJ 149—2006[S]. Beijing：China Building Industry Press，2006：36.

（责任编辑：邓光辉）

Finite Element Analysis of the Torsional Effect of Short-Limb Shear Walls

ZHOU Lei，YANG Xiaohua，LU Xuechen
（School of Civil Engineering of Hunan University of Technology，Zhuzhou Hunan 412007，China）

PA fi nite element model of a three-layered short-limb shear wall space structure has been established by using ANSYS software. By modifying the controlling parameter and stress condition, a research has been conducted on the in fl uence of axial compression ratio, load eccentricity and stirrup reinforcement ratio in node areas on the torsional bearing capacity of short-limb shear walls, followed by a comparison between the experimental results and those of a structural model test. The conclusion shows that: the torsional bearing capacity of short-limb shear walls increases with the increase of axial compression ratio with its value at or under 0.5, while the torsional bearing capacity of short-limb shear walls decreases with the increase of axial compression ratio with its value above 0.5. The torsional effect has been strengthened and the structural bearing capacity has been reduced with the increase of the load eccentricity. The increase of the torque increases the tensile failure of the end of external structure of coupling beams under ending shear torsion, which makes the external structure a vulnerable place for seismic resistance that requires reinforcement. An appropriate increase in stirrup reinforcement ratio will effectively improve the torsional bearing capacity of structures.

short limb shear wall space structure；torsional effect；axial compression ratio；load eccentricity；stirrup reinforcement ratio in node areas

U398+.2

A

1673-9833(2017)02-0028-05

10.3969/j.issn.1673-9833.2017.02.005

2016-11-31

周 磊（1992-），男，江苏无锡人，湖南工业大学硕士生，主要研究方向为高层建筑结构，E-mail：690032140@qq.com