国家电网电容器投标报价模型
刘增杰,祝方才,黄金霞
(1.湖南工业大学 土木工程学院,湖南 株洲 412007;2.湖南工业大学 理学院,湖南 株洲 412007)
国家电网电容器投标报价模型
刘增杰1,祝方才1,黄金霞2
(1.湖南工业大学 土木工程学院,湖南 株洲 412007;2.湖南工业大学 理学院,湖南 株洲 412007)
针对国家电网的综合评标法的投标报价得分算法,运用数理统计分析了2013年第5批至2014年第3批共5批数据的货物清单与各批部分包中的价格得分情况,得出2014年第3批货物清单与合容电气的投标报价确定每类货物的平均报价,提出改进的非合作模式下浮比例可变投标报价模型;运用马氏链算法计算2014年第4批的预算价格,并运用该模型预测了2014年第4批给定包的预算价格;最后提出国家电网招投标方法改革的合理化建议。
投标报价模型;数学建模;最优报价;减分速率指数;下浮比例;综合评标法
0 引言
随着国家的基础设施建设进一步扩大,国家电网建设所用的电容器采购方式采用招标投标形式,招标投标在国家及企业建设的物资采购中应用越来越广。随着招标投标所面对的经济对象不断大型化、复杂化和招投标行为的多批次化,给投标商带来新的挑战。如何依据招标单位的评标方法,在分析竞争对手过去已有的报价数据基础上构建有效的投标报价模型,并以此为依据制定出既有最优利润又有较高中标率的合理报价,成为投标企业生死攸关的大事,从而引起了众多学者的广泛关注[1-3]。邓铁军等[4]在综合评标法的基础上,以数理统计原理和模糊数学综合评判理论为依据提出了工程投标最优报价的报价策略模型。谢小波等[5]提出了利用数理统计的回归分析理论,确定其报价函数以及优势报价区间。樊建强等[6]基于贝叶斯博弈均衡理论,针对合理低价评标法,从双方博弈和多方博弈两个角度建立了最优化投标报价模型。
根据国家电网电容器投标计划,国家电网于2013—2015年每年举行6批电容器类货物的招标,每批又分若干包,不同包包含的电容器规格、数量不同。依据以往数据显示,参加投标厂家每年基本固定,主要厂家有17家。国家电网在2013—2014年采用的是综合评标法进行招标。该评标办法中,技术、价格、商务占的比例分别为30%, 60%, 10%,以总分100分计。假定各厂家在技术、商务方面实力基本相当,因此此问题中各厂家只需考虑通过合理的投标报价提高价格得分,得到价格得分第一就认为中标。各投标厂家具体得分情况以区间平均下浮双边曲线算法计算。
1 区间平均下浮双边曲线算法
1.1 计算原则
对于某批次某包中基准价的计算区间,以该包中各厂家全部有效投标报价算术平均值A的80%~115%为基准区间,根据不同批次各包投标报价的不同情况可分为以下3种情况,其中以A1作为有效报价的算术平均值。
1)若在某一批次的某一个包中的投标报价全部在基准区间内,则A1表示该包全部投标报价的算术平均值,以B作为基准价,则B=A1×(1-a),其中a为下浮比例(或称下浮系数、价格下浮基准点);
2)若在某一批次的某一个包中的投标报价既有在基准区间内的也有在区间外的情况,则先剔除区间外的报价,以全部基准区间内的有效投标报价算术平均值作为A1,计算基准价B=A1×(1-a);
3)若在某一批次的某一个包中的投标报价都在此区间外,则所有基准区间外的投标报价即为有效投标报价,计算算术平均值A1,基准价B=A1×(1-a)。
1.2 区间平均下浮双边曲线算法的价格得分
求所有参与投标报价厂家出价的算数平均数A,设某种配备货物有N个公司参加报价,报价分别为xi(i=1, 2, …,N),则。
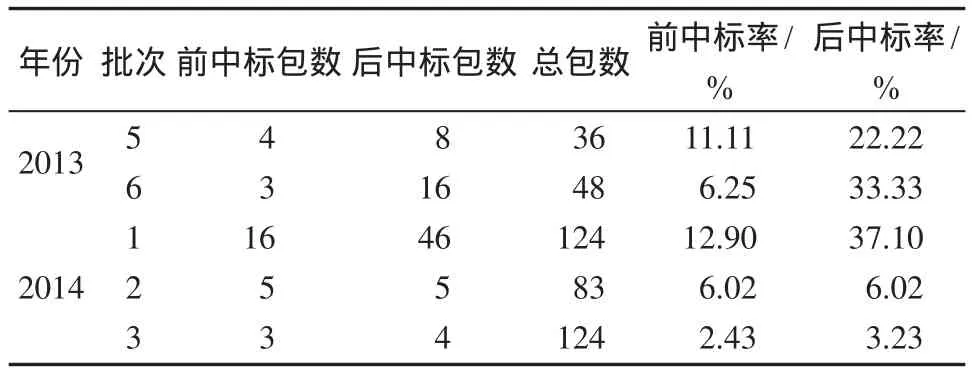
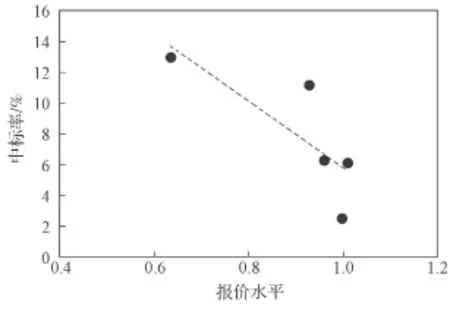
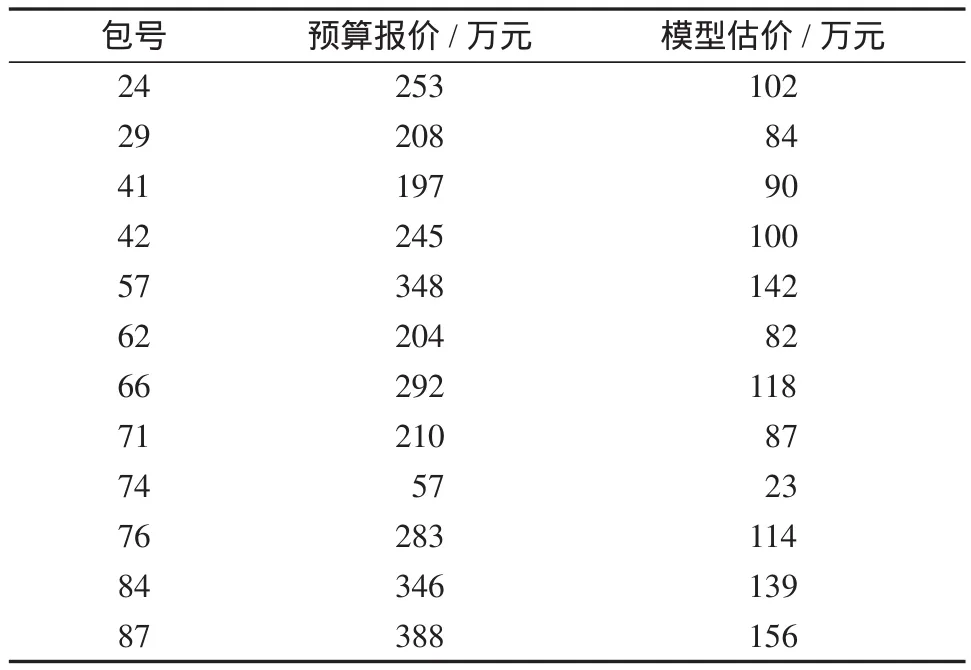
求算数平均数A1。A1表示所有参与投标报价厂家的出价中落在有效基准区间内的价格的算术平均值。设参加该种配备货物报价的N个公司有M个公司的报价均落入(0.8A, 1.15A)有效基准区间(即0 当M=N时(即参加该种配备货物报价的N个公司全部落入(0.8A, 1.15A)有效基准区间内时),有A1=A,基准价B=A1×(1-a); 当M=0时(即参加该种配备的货物报价的N个公司全部落入有效区间(0.8A, 1.15A)外时,有A1=A,基准价B=A1×(1-a)。 价格得分计算公式为: 当P≥B,得分DF=(B/P)n; 当P 式中:P为投标人的评标总价; m,n为减分速率指数。本例中n,m取值有2种情况:n=1.5,m=0.6;n=2.0,m=0.3。 2.1 计算方法 在非合作模式下浮比例可变投标报价模型[7]中,假设第i批中某种配置的货物所有投标报价的厂家共ni个,另设需要帮助设计投标的厂家(以下用甲厂家表示)原报价为xi,ni,其余ni-1个厂家报价分别为xi,1,xi,2, …,xi,ni-1,故在基本假设中假设所有报价均在有效报价区间,以此为例计算基准价为 Bi为第i批中某种配置的货物所有投标报价的基准价。 设Ai为第i批中某包配置的货物投标报价的算术平均值,为使甲厂家价格报价得分最高,设甲厂家投标报价为Hi,则Hi为最优报价,有 若全部报价均落在有效报价区间,以A1i表示第i批货物某包的有效投标报价算术平均值,则 相应的该批货物基准价Bi′为 由价格计算得分公式分析可知,报价越接近基准价,得分越高,因此最优报价为 联立式(2)~(5),可得 运用式(6)进行编程,对以往各厂家投标报价数据中给出的每一批的每个包的数据进行计算,整理得出运用上述模型程序计算前后不同批次的中标率,如表1所示。 表1 中标率对比Table 1 Contrast of successful bidding ratios 在已知竞争对手的投标报价基础上,可以得出基于式(6)的最优投标报价模型。但实际应用中,竞争对手的投标报价是未知的,各投标厂家是在非合作模式下的竞标,该模型不能对下一次厂家投标报价进行有效指导,需要进一步改进。 2.2 定量分析的方法与步骤 分析甲厂家历年来的投标报价资料,用数理统计的方法[8],统计计算报价水平与投标成功率的关系,绘制报价与中标率的散点分布图,然后利用数学回归拟合的方法,分析得出报价水平与中标率的相关关系数学公式,以此为投标报价决策提供理论依据。 首先,计算出投标单位j在历次投标中所有报价的平均值,为(A1j,A2j, …,Anj),则Nij=Bij/Aij。其中Nij为投标单位j在第i次投标中的标准标价比值,Aij为投标单位j在i次投标报价的平均值;Bij为投标单位j在第i次投标的报价。 然后计算投标单位j在各次投标中标准价比值的平均值,也为平均标价比值。若投标单位j已投n次标,则 设投标单位j在n次投标中成功的次数为Vj,则该单位的中标率Pj=Vj/n; 报价水平与中标率统计见表2。 分别以报价水平和中标率为x,y坐标建立直角坐标系,绘制报价水平-中标率数理统计散点分布图,如图1所示。 表2 报价水平与中标率统计Table 2 Statistics of the quotation levels and successful bidding ratios 图1 报价水平-中标率散点分布图Fig. 1 Scattered plots of the quotation levels and bid-winning rates 确立报价水平x与中标率的数学模型后,可以找到x与y之间的关系,但回归的非线性曲线能否确切反应报价水平与中标率之间的关系及其关系密切程度,需要计算回归方程与(Xi,Yi)的相关系数来验证。假设统计投标单位的个数为m,统计值为(xi,yi),(Xi,Yi)的线性化算数平均数为,计算相关系数R的过程如下。 设LXX,LYY,LXY分别为: 相关系数 R反应了回归方程与(Xi,Yi)关系的密切程度,有以下结论。 当LXY=0,R=0,此时Y的变化与X无关,即X与Y不存在线性关系。 当0<|R|<1,X与Y之间存在一定的线性关系,R的绝对值越小,其关系密切程度越小;反之,密切程度越高。 当|R|=1,X与Y为完全线性关系;R=1时,为完全正相关;R=-1时,为完全负相关。 对图6的散点分布图进行拟合计算得出基于回归分析的线性拟合结果Y=a+bx,其中b=0.770 887 8,a=0.775 867 199。 由以上分析可知,选定所想达到的中标率,并依据模型推出报价水平,若已知下一批次的投标次数n与平均报价即可逆向推导出下一批的预测报价。 将往年投标报价中标结果代入分析模型验证,本文提出的模型是合理可行的,代入2014年第3批数据验证发现经过本文国家电网电容器投标报价模型调整后的报价结果较未经调整的报价最终中标率2.43%,约提高了33%,达到了3.23%。另外该模型是基于数理统计的方法得出的,统计数据量越大,则预测的结果越准确。 本文以湖南省第二届研究生数学建模竞赛的试题为依托,题目中未给出厂家对各类货物的直接报价,故采用马尔科夫链算法,根据往年的投标报价估算该厂家各类货物的平均价格用于计算。 马尔科夫分析法认为某一系统在现在情况已知的情况下,系统未来时刻的情况只与现在的状况有关,与过去的历史无直接关系。而该项目的报价也存在以下特点:1)配置相同的包(货物类型相同,数量相同、下浮比例也相同的包)在不同投标批次中报价不同;2)下一批次合包的报价受到当前批次的报价情况的影响,即2014年第4批各包报价受2013年第3批各包报价的影响。故2014年第4批各包的每类货物的报价由2013年第3批各包的每类货物的平均报价所决定。 设状态概率πj(k)表示的是事件在历史状态为已知的条件下,经过k次状态转移后,第k个批次处于的状态Ej的状态概率。从初始状态开始,经过k次状态变换后达到状态Ej的这一状态转移过程,pij为在转移过程的条件概率,根据马尔科夫过程的无效性及条件概率公式有 若行向量为π(k)=[π1(k),π2(k), …,πn(k)],再由式,可得到以下的公式 式中:以P代替各转移过程对应的条件概率pij; π(0)为初始状态概率向量。 设2013年第3批中有m个由n种同类型组成的包,设aij为第i个包中的第j类货物的数量,bj为该包的报价。建立如下线性方程组: 记系数矩阵为A,未知量矩阵为X,报价矩阵为B,线性方程组变为AX=B;求解后再综合考虑转移概率即可得到每类货物的平均报价。计算2014年第4批给定包的预算价格,并将预算价格带入所建立的模型中求解调整后的预算价格与模型估价,结果见表3。 表3 预算价格与模型估价计算结果Table 3 A diagram of budget prices and calculation results from the valuation model 对比表3中的结果可知,预算报价和模型估价的差别较大,且经过验证该模型报价结果对中标率有一定提高,故在保证盈利的前提下,可采用模型估价以提高投标的中标率。 对于投标企业来说投标报价策略与决策事关企业的兴衰与生死存亡,一个合理的投标报价模型是提高投标中标率的关键,决定着企业经济效益并影响着企业未来的发展。本文对国家电网电容器投标的2013年第5批至2014年第3批电容器发货清单与各批部分包的价格得分情况,结合国家给出的各种型号电容器的最高限价进行了分析,运用数理统计与马尔科夫分析法建立了改进的非合作模式下的下浮系数连续批次投标报价模型。该模型可对投标报价的预测和调整起到一定的指导意义,增加投标报价的中标率。研究组在模型分析的基础上对国家电网招投标方法的改革提出如下建议: 1)通过对国家电网综合评标法评标的价格得分算法分析,国家招投标方法改革应趋向于降低国家电网建设的投资。国家电网可以通过对下浮比例的增加来降低各个投标厂家的整体价格得分,从而减少国家电网的建设成本; 2)通过降低减分速率指数m,同时增加减分速率指数n,来驱使投标商降低投标报价来获得较高的报价得分,从而使区间平均下浮双边曲线算法计算的基准价降低,使国家电网低价购得同样数量与质量的电容器; 3)综合评标法中的区间平均下浮双边曲线算法的区间范围可适当减小。 [1] 郝丽萍,谭庆美,戈 勇. 基于博弈模型和模糊预测的投标报价策略研究[J]. 管理工程学报,2002,16(3):94-96. HAO Liping,TAN Qingmei,GE Yong. Study on Strategies Making of Project Offering Based on Game Model and Fuzzy Forecasting[J]. Journal of Industrial Engineering,2002,16(3):94-96. [2] 刘庆明. 弗里德曼模型在电网建设投标报价中的应用研究[D]. 北京:华北电力大学,2010. LIU Qingming. Application Research of Friedman’s Model in Bidding of Grid Construction[D]. Beijing:North China Electric Power University,2010. [3] 郭清娥,王雪青. 基于交叉评价和模糊控制理论的工程项目投标决策方法研究[J]. 运筹与管理,2012,21(6):100-104. GUO Qing’e,WANG Xueqing. A Decision Making Method for Bidding of Construcation Projects Based on Cross-Evaluation and Fuzzy Theory[J]. Operations Research and Management Science,2012,21(6):100-104. [4] 邓铁军,欧 莉,龚亮英. 工程投标报价策略模型的研究及应用[J]. 株洲工学院学报,2004,18(5):57-60. DENG Tiejun,OU Li,GONG Liangying. Analysis and Application of the Strategy Model for Project Quotation[J]. Journal of Zhuzhou Institute of Technology,2004,18(5):57-60. [5] 谢小波,张井泉,王月明,等. 回归分析法在投标报价中的应用[J]. 四川建筑,2010,30(3):247-249. XIE Xiaobo,ZHANG Jingquan,WANG Yueming,et al. The Application of Regression Anslysis Methed in the Tender Offer[J]. Sichuan Architechure,2010,30(3):247-249. [6] 樊建强,徐海成. 基于贝叶斯博弈均衡的合理低价中标下投标报价模型[J]. 统计与决策,2008(18):65-67. FAN Jianqiang,XU Haicheng. Bidding Model of Bidding Price Based on Bayesian Game Equilibrium[J]. Statistics and Decision,2008(18):65-67. [7] 冯卫兵. 非合作模式下动态下浮比例连续批次投标报价模型二[J]. 西安科技大学学报,2015,35(4):505-510. FENG Weibing. Dynamic Fall Ratio Consecutive Batch Bidding Model of Non-Cooperative Mode[J]. Journal of Xi’an University of Science and Technology,2015,35(4):505-510. [8] 徐立新,张新成,吴相林. 基于数理统计的工程投标决策定量分析方法及应用[J]. 计算机工程与应用,2006,42(8):204-206. XU Lixin,ZHANG Xincheng,WU Xianglin. A Quantitative-Analysis Method for Engineering Bidding Decision and It’s Application Based on Mathematical Statistics[J]. Computer Engineering and Applications,2006,42(8):204-206. (责任编辑:申 剑) A Price-Bidding Model for National Grid Capacitors LIU Zengjie1,ZHU Fangcai1,HUANG Jinxia2 In view of the bidding scoring algorithm adopted by the State Grid for a comprehensive evaluation, an analysis has been made, by using mathematical statistics, of the cargo list and price scoring concerning the statistics of fi ve batches, namely, from the fi fth patch in 2013 to the third patch of 2014. An average quotation can be obtained of the cargo list of the third patch in 2014 and the tender offer of the capacitive electricity. An improved bidding model under variable ratio has thus been established in the non-cooperative mode. A budget price of the fourth batch in 2014 will be worked out by using Markov chain algorithm, and a prediction of its budget price of the given packages can be achieved. Finally, some reasonable proposals have been made for the National Grid bidding method reform. bidding model;mathematical model;optimal price;reduced rate index;downward fl uctuation;comprehensive evaluation method TU723.2 A 1673-9833(2017)02-0084-05 10.3969/j.issn.1673-9833.2017.02.015 2016-12-11 刘增杰(1991-),男,河北石家庄人,湖南工业大学硕士生,主要研究方向为岩土加固技术,E-mail:1656347587@qq.com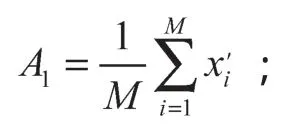
2 非合作模式下浮比例可变投标报价模型

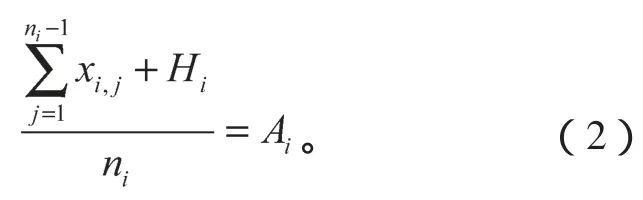



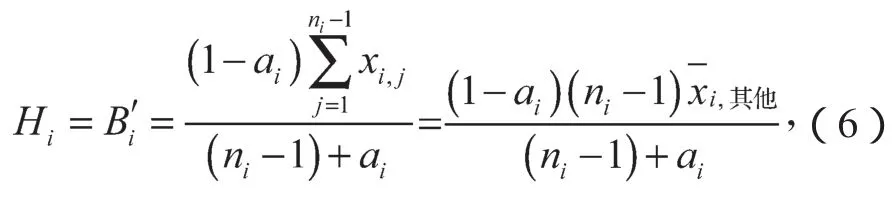
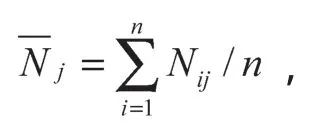

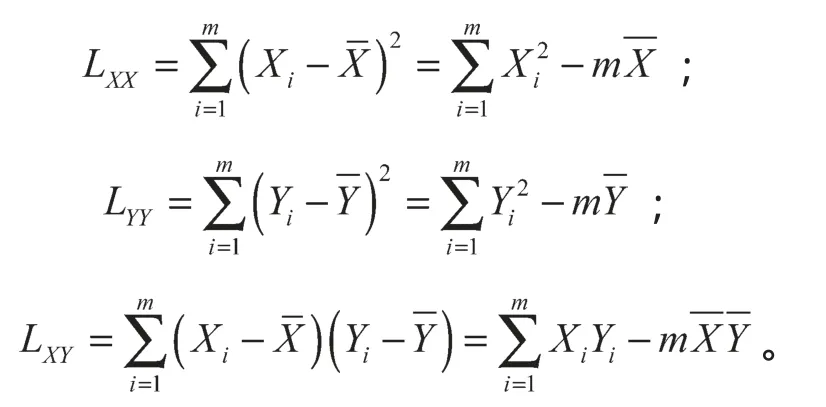

3 马尔科夫分析法计算各类货物平均报价


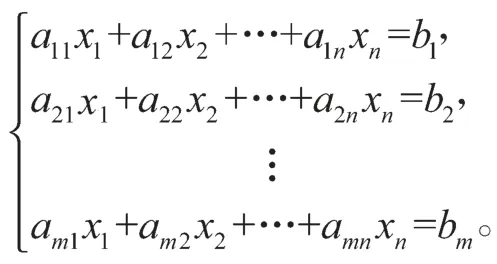
4 总结与建议
(1. School of Civil Engineering,Hunan University of Technology,Zhuzhou Hunan 412007,China;2. School of Science,Hunan University of Technology,Zhuzhou Hunan 412007,China)

