“图形与几何”试题精选

“图形与几何”试题精选

一、填空题

1.观察图1，将阴影部分与整个图形面积的关系分别用分数、 最简整数比、百分数表示：

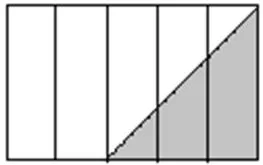
图1

2.把一张正方形的纸连续对折4次，折后的每一小块占这张正方形纸的（ ）。

3.小明搭了一个立体图形，从正面看到的形状是图2①，从上面看到的形状是图2②。搭一个这样的立体图形，最少需要（ ）个小正方体。

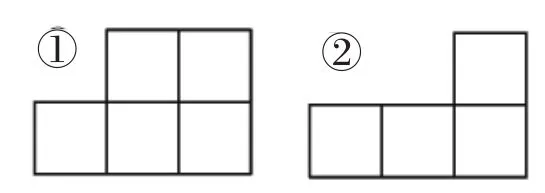
图2

4.如图3，拉动平行四边形的邻边后，它的面积会发生变化。当拉成（ ）形后，它的面积最大，最大面积是（ ）平方厘米。

图3

5.按照图4的方法拼下去（单位：厘米），第九个图形的周长是（ ）厘米。

图4

6.根据图5提供的信息可以知道，一个暖水瓶（ ）元， 一个水杯（ ）元。

图5

7.把一个圆沿半径剪成若干等份，拼成一个近似平行四边形（如图6），近似平行四边形的周长比圆的周长增加了20厘米，圆的面积是（ ）平方厘米。

图6

8.一种机器零件（如图7），圆柱部分和圆锥部分的体积比是（ ）。如果圆柱部分的体积是48立方厘米，这个零件的体积是（ ）立方厘米。

图7

9*.同学们，在我们小学阶段学到了很多数学知识，知识之间都有着密切的联系。比如长方体和正方体的关系可以用图8表示，除此以外，还有哪些知识之间的关系也可以用这样的图（如图9）表示？

图8

图9

若A是长方形，那么B可以是（ ）。

若B是长方形，那么A可以是（ ）。

除了上面的例子，你还能再写一组这样的关系吗？

如果A是（ ），那么B是（ ）。

10*.长方体的右侧面面积是12平方厘米，前面面积是8平方厘米，上面面积是6平方厘米。这个长方体的长、宽、高分别是（ ）厘米、（ ）厘米、（ ）厘米。

11.大课间活动，李老师和乐乐、棒棒、康康、盈盈、晶晶在操场上做游戏，所站的位置如图10所示。李老师的两边是乐乐、棒棒，李老师的正对面是康康，棒棒和晶晶不相邻，乐乐和盈盈不相邻。那么站在A位置的是（ ），站在C位置的是（ ）。

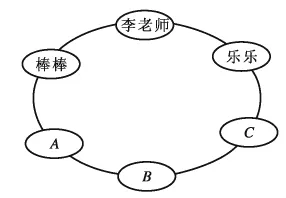
图10

12.图11是一个六边形，从A点开始将图形切割成数个三角形。

（1）六边形被切割成（ ）个三角形。

（2）每个三角形的内角和是（ ）度。

（3）只要把所有三角形的内角加起来，刚好就等于六边形的内角和，因此我们知道，n边形的内角和可以用式子记成（ ）度。

图11

二、选择题

1.下面图（ ）可能是图12这个单孔纸箱的展开图。

图12

2.如图13，在一个底是 8分米，高是6分米的平行四边形内画一个面积最大的三角形，这样的三角形可以画（ ）。

A．0个 B．1个

C．2个 D．无数个

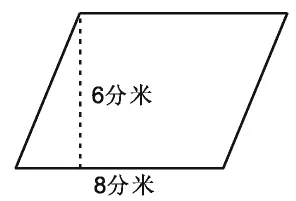
图13

3.如图14，各杯中饮料最多的是（ ）。

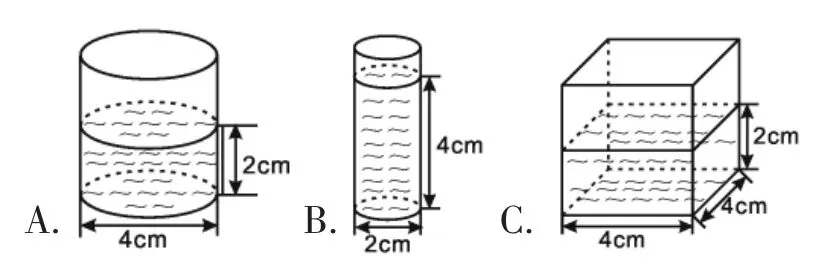
图14

4.玩一个搭积木游戏，每次增多的积木的个数相同，所搭成的积木形状如图15所示。根据规律，搭第8次一共需要积木（ ）个。

图15

A.24 B.21 C.27

5.图16是一个长3厘米，宽与高都是2厘米的长方体。将它挖掉一个棱长1厘米的小正方体，它的表面积（ ），体积（ ）。

A.比原来大 B.比原来小

C.不变 D.无法确定

6.一个圆形花坛内种了三种花 （如图17），用条形图表示各种花占地面积的关系应该是（ ）。

图17

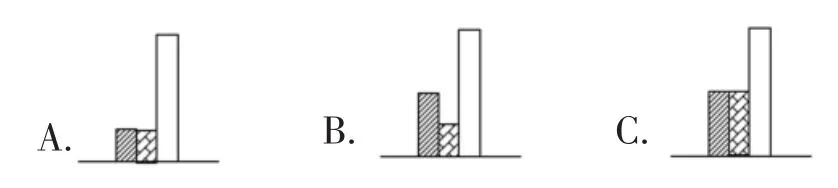
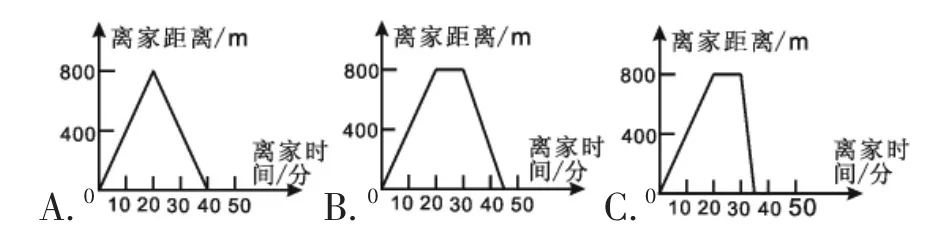
7.小强经常到离家800米远的沿河公园进行体育锻炼，他步行20分钟到公园，然后在公园的双杠上锻炼10分钟，最后用5分钟时间跑步到家。下面各图中，能正确描述小强离家时间和离家距离关系的是（ ）。

8.如图18，把圆柱体切拼成长方体，切拼后图形的体积和表面积（ ）。

图18

A.不变

B.体积不变，表面积变大

C.体积不变，表面积变小

9．如图19，三角形AOB、BOC、COD分别是同一个圆中的钝角三角形、锐角三角形、直角三角形。这三个三角形的面积相比较，（ ）。

图19

A.钝角三角形大 B.锐角三角形大

C.直角三角形大 D．三个三角形一样大

10.一盒酸奶，外包装是长方体形状，包装纸上标注“净含量650mL”。实际量得外包装长8厘米，宽5厘米，高15厘米。根据以上数据，你认为标注的净含量是（ ）。

A.真实的

B.虚假的

C.无法确定真假的

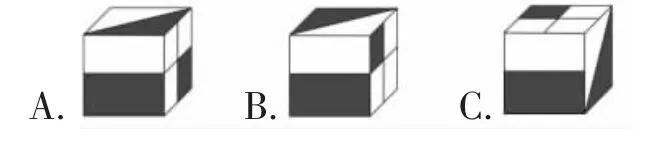
11.一个正方体，有三个面上分别画上了一个图形（如图20）。把这个正方体像图21那样翻动一下，得到的图形正确的是（ ）。

图20

图21

三、解答题

1*.我们知道，三角形的内角和是180°，一个平角也是180°，请你利用以上两个结论完成下列各题：

（1）如图22①，延长三角形ABC的边BC到点D，请探究∠ACD、∠A、∠B三者之间的关系，并说明理由。

（2）如图22②，已知∠A=40°，∠B=21°，∠C= 18°，求∠BDC的大小。

图22

2*.如图23所示，正方形ABCD和等腰直角三角形EFG中，∠F=90°，EG=AB=4厘米，且E、G、A、B在同一条直线上。若起始位置GA=3厘米，三角形EFG以每秒1厘米的速度向右平移t秒，求t为多少时，三角形EFG与正方形ABCD的重叠部分的面积等于0.5平方厘米。

图23

3*.如图24，在一个棱长为20厘米的正方体密闭容器的下底固定了一个实心圆柱体，当容器内盛有m升水时，水面恰好与圆柱体的上底面平齐。如果将容器倒置，则圆柱体有8厘米露出水面。已知圆柱体的底面积是正方体底面积的求实心圆柱体的体积。

图24