滚筒洗衣机悬挂系统动力学建模与实验

王 豪 刘 雷

南京航空航天大学机电学院，南京,210016



滚筒洗衣机悬挂系统动力学建模与实验

王 豪 刘 雷

南京航空航天大学机电学院，南京,210016

考虑上配重对洗衣机悬挂系统振动的影响，基于拉格朗日方程，对该系统进行动力学建模。进行了多工况下的洗衣机筒体振动测量实验，以实验得到的筒体振幅随转速变化的关系曲线为目标，对数学模型进行了参数修正。通过数值仿真与实验结果的对比分析，验证了动力学模型的正确性。

滚筒洗衣机;悬挂系统；上配重；动力学模型；振动测量

0 引言

滚筒洗衣机脱水时的振动大小直接影响消费者的体验，是衡量洗衣机性能优劣的重要指标。为研究其振动问题，可以将滚筒洗衣机悬挂系统看作一个多自由度振动系统。对该系统进行动力学建模，可以明确分析各参数对洗衣机振动的影响，便于开展减振方法的研究。

文献[1]运用拉格朗日方程建立了洗衣机三自由度平面运动微分方程，并基于振型叠加法推导了方程动力响应的求解公式，利用公式可以较为方便地进行系统动力学分析。文献[2]利用矢量法和拉格朗日方程建立了洗衣机系统六自由度动力学模型，利用该模型进行数值仿真，分析了各关键部件对洗衣机振幅的影响规律。文献[3]运用第二类拉格朗日方程，建立了带有磁流变阻尼器的滚筒洗衣机平面振动模型，通过数值求解分析了瞬态脱水振动特性，提出了振动控制综合效果较好的加速时间常数。文献[4]运用拉格朗日方程建立了洗衣机六自由度悬挂系统的动力响应方程，为虚拟样机仿真分析提供了理论依据。文献[5]运用牛顿第二定律建立了滚筒洗衣机关于旋转平面的动力学方程，通过试验验证了模型正确性，并基于遗传算法对洗衣机参数进行了优化设计。

以往的数学建模通常将滚筒洗衣机外筒上部配重的质量并入筒体，仿真结果显示此时筒体水平振幅与垂向振幅接近。而实际洗衣机运行时，上配重相对于筒体是个不平衡质量，会导致筒体垂向振幅明显大于水平振幅。本文通过拉格朗日方程建立了滚筒洗衣机的三自由度振动微分方程，建模时将上部配重与筒体分开，单独考虑上配重动能与势能，使得数学模型能够反映实际洗衣机的这一振动特性。同时，本文进行了多工况下的洗衣机筒体振动测量实验，以实验测得的筒体振幅随转速变化的关系曲线为目标，对数学模型参数进行了修正，使其在多工况下脱水的稳态响应与实际情况基本一致。

1 悬挂系统力学模型

1.1 基本假设

滚筒洗衣机悬挂系统由外筒、内筒、弹簧、阻尼、配重以及电机等组成，作如下假设：①将悬挂弹簧和阻尼器视为理想元件，忽略其质量和运动副间的摩擦力(阻尼器除外)；②将外筒、前配重以及电机组视为一个整体，统称为外筒；③将外筒与内筒视为刚体，旋转轴为同一轴线；④弹簧与箱体，阻尼器与箱体的连接点为固定点；⑤脱水工作时，衣物视为定质量质点，且与内筒保持相对静止；⑥悬挂系统做平面运动，忽略其沿筒体旋转轴方向的振动。根据以上假设建立的力学模型如图1所示。

图1 滚筒洗衣机悬挂系统力学模型Fig.1 Physical model of drum type washing machine’s suspension system

图1中，mD1为外筒质量;mD2为内筒质量；m1为偏心衣物质量;m2为上配重块质量;ω为内筒转速;φ1、φ2分别为静平衡时悬挂弹簧、阻尼器与y方向的夹角;L0、n0分别为静平衡时悬挂弹簧、阻尼的长度;e为偏心质量旋转半径;x、α、θ为悬挂系统自由度。

1.2 动力学方程

应用拉格朗日方程建立振动微分方程[6]：

(1)

j=1,2,…,N

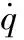
(1)悬挂系统动能为

(2)

式中，vG为外筒和内筒的质心速度；vm1为偏心质量质心速度；vm2为上配重质心速度；I1、I2、I3分别为外筒、内筒、上配重的转动惯量。

(2)悬挂系统势能为

(mD1+mD2+m1)gΔh+m2gΔh1

(3)

式中，Δh为将外筒、内筒、偏心质量看作整体后其质心的高度变化；Δh1为上配重质心的高度变化；k1为悬挂弹簧的刚度;g为重力加速度。

(3)悬挂系统能量散失函数。通常情况下，假设悬挂系统阻尼为黏性阻尼，黏性阻尼力与速度成线性关系，能量散失函数即为阻尼力在位移x3、x4上做的功，有

(4)

(4)悬挂系统振动微分方程。由于偏心质量产生的激振力已经表达为系统的动能和势能形式，因此在式(1)等号右边不再重复考虑这些激振作用力。应用矢量分析法对悬挂系统进行运动分析，点的位置矢径对时间的一阶和二阶导数分别为点的速度和加速度向量。将系统动能、势能以及能量散失函数表示为广义坐标x、α、θ的函数，然后代入式(1)，根据小位移假设理论，整理可得系统的振动微分方程：

(5)

I1+I2+I3

m12=m21=0

m13=m31=-M′(ccosφ1-h1sinφ1)-

m2(h1+h3+h0)sinφ1m23=m32=-M′(csinφ1+

h1cosφ1)L0+m2(h1+h3+h0)cosφ1L0

r11=2r1(cos2φ2cos2φ1+sin2φ2sin2φ1)

r33=2r1[c2cos2φ2+d2cos2φ2+(h1+h2)2sin2φ2-

2d(h1+h2)cosφ2sinφ2]

r12=r21=2r1L0cosφ1sinφ1cos2φ2

r13=r31=2r1[-ccos2φ2cosφ1+

(h1+h2)sin2φ2sinφ1-dcosφ2sinφ2sinφ1]

r23=r32=2r1L0[-ccos2φ2sinφ1-

(h1+h2)sin2φ2cosφ1+dcosφ1sinφ2cosφ2]

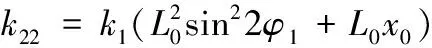
k33=4k1c2cos2φ1+Mgh1-m2g(h0+h3)

k12=k21=k1L0sin2φ1cos2φ1

k13=k31=-2k1ccosφ1cos2φ1

k23=k32=-2k1L0ccosφ1sin2φ1

M′=mD1+mD2+m1+m2

M=mD1+mD2+m1

通过观察可以发现，悬挂系统振动微分方程是耦合的，且矩阵中包含较多的结构参数，这给求解析解带来很大困难。为此，本文采用Runge -Kutta法求得该悬挂系统振动微分方程的数值解。

2 洗衣机振动测量实验

通常我们忽略洗衣机滚筒的轴向振动[7]，把洗衣机滚筒看作刚体，用滚筒上的点在悬挂平面中的运动状态直观地反映悬挂系统的运动状态，尤其是滚筒质心。本文考虑实验可行性，选取洗衣机外筒正上方一点作为测量点，以该点的振动响应表征洗衣机悬挂系统的振动响应。通过加速度计测量该点水平和垂向振动加速度，数据采集卡将采集到的信号输入电脑，通过LabVIEW生成信号文件，处理后得到该点水平和垂向振动位移以及运动轨迹。

表1所示为实验仪器参数。图2、图3分别为系统测试原理图和数据处理流程图。根据该型号洗衣机脱水转速模式与洗衣重量设定了20种工况，如表2所示。本次实际称取的衣物质量分别为0、1.060 kg、2.015 kg、2.955 kg、4.075 kg，见表3。

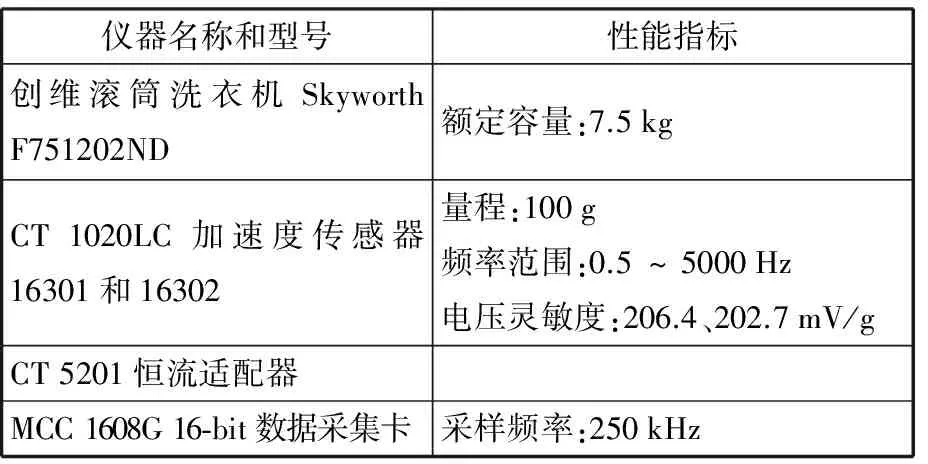
表1 实验仪器

图2 测试系统原理图Fig.2 Schematic of measurement system

图3 数据处理流程图Fig.3 Flow chart of data processing

表2 工况列表

表3 衣物列表

设置采集卡采样频率为300 Hz，编号16301和16302的两个传感器分别测量出每种工况下该点在悬挂平面内的水平加速度信号和垂向加速度信号。

以工况Test15为例，最终得到的该点水平和垂向振动位移-时间曲线如图4、图5所示，以水平位移信号为横坐标，垂向位移信号为纵坐标，可以得到该工况下测量点的运动轨迹，如图6所示。若数学模型仿真得到的测量点振动稳态响应与实验测量的一致，则说明数学模型能够较好地反映物理样机的振动特性。

图4 Test15测量点水平振动位移-时间曲线 Fig.4 The curve of xt-t under Test15

图5 Test15测量点垂向振动位移-时间曲线 Fig.5 The curve of yt-t under Test15

图6 Test15测量点运动轨迹 Fig.6 Movement path of drum under Test15

3 数学模型参数修正及仿真与实验对比

建立力学模型时进行了各种理想假设，现对数学模型工作状态也进行如下假设：①洗衣机本身所有参数固定且不受输入工况的影响；②对于一种工况，确定了偏心衣物质量，其质心的旋转半径也就固定，这一工况参数也和模型本身参数一样不受输入转速的影响。

如表4所示，洗衣机的固定参数有尺寸、弹簧刚度、阻尼系数、各部分质量和转动惯量等，数学模型直接调用这些参数。

表4 滚筒洗衣机参数

3.1 数学模型参数修正

实验中衣物体积随质量变化而变化，衣物质心旋转半径也随之改变。以往的数学模型中，将衣物抽象为偏心质点，通常以内筒内侧半径为该质点旋转半径，这与实际情况差距较大，因此需要对数学模型中偏心质量质心的旋转半径进行修正。

基于工作状态的假设，偏心衣物质心旋转半径不受洗衣机转速的影响，只与衣物质量相关。实验共有20种工况，将衣物质量相同的4种工况合并为一组工况，共5组工况。整理实验数据，可以得出每组工况下筒体测量点振幅平均值随转速变化的趋势，部分如图7所示。

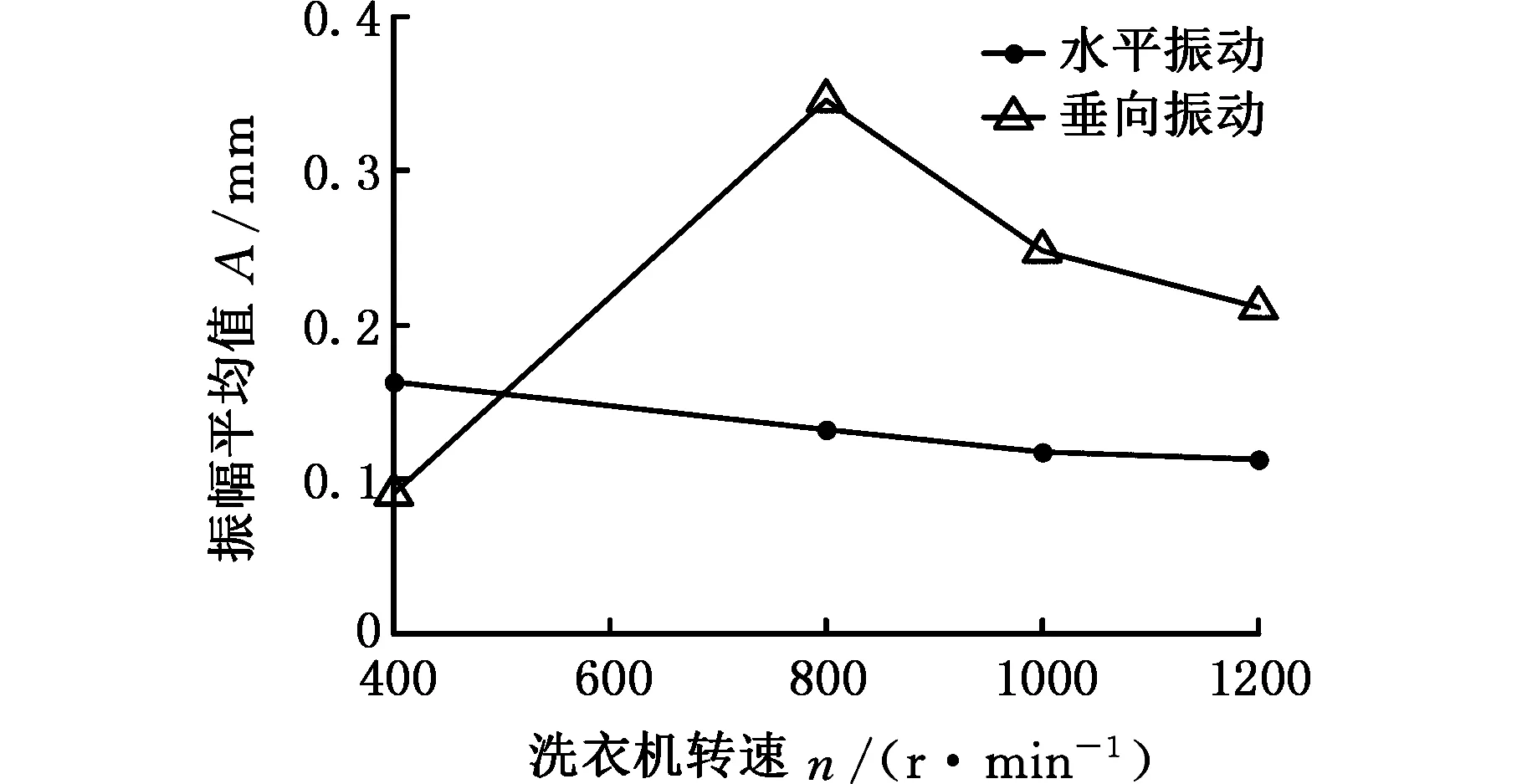
(a)m1=0

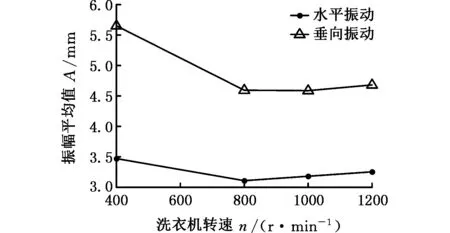
(b) m1=2 kg

(c) m1=4 kg图7 测量点振幅平均值-转速曲线Fig.7 The curve of A-n

以上述曲线为目标来修正数学模型参数，即在每一组工况下，以测量点的水平和垂向仿真振幅平均值组成向量f=(f1,f2,…,f8)，其中f1，f2，f3,f4分别为转速在400 r/min，800 r/min，1000 r/min，1200 r/min时仿真水平振幅平均值，f5，f6,f7，f8为各转速下仿真垂向振幅平均值，以实验测得的振幅平均值组成目标向量g=(g1,g2,…,g8)，其中g1，g2,g3，g4分别为转速在400 r/min，800 r/min，1000 r/min，1200 r/min时实测水平振幅平均值，g5，g6,g7，g8为各转速下实测垂向振幅平均值，这两个向量的距离为

以此来表征仿真和实验结果的相似程度，建立该距离关于偏心质量质心旋转半径的函数:

找出距离最小时的偏心质量质心旋转半径，通过编程求得该距离函数与旋转半径的关系曲线如图8所示。

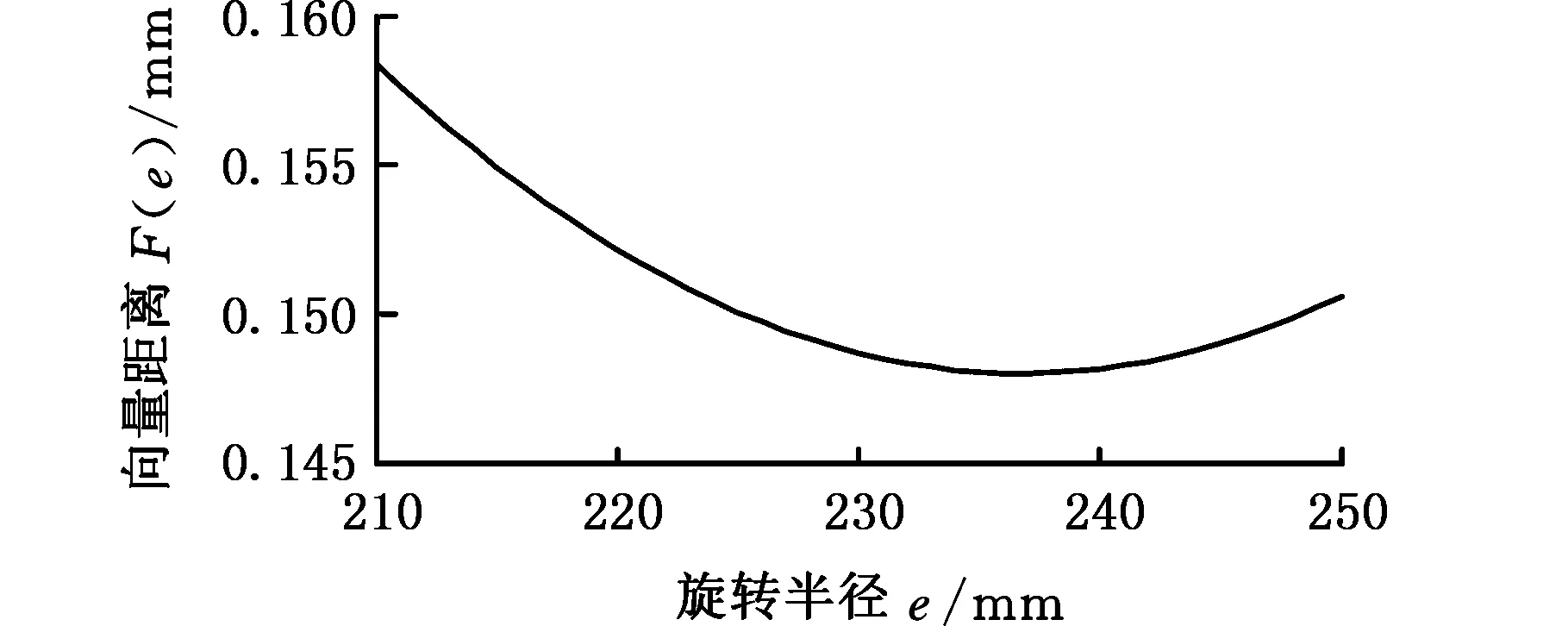
(a)m1=0

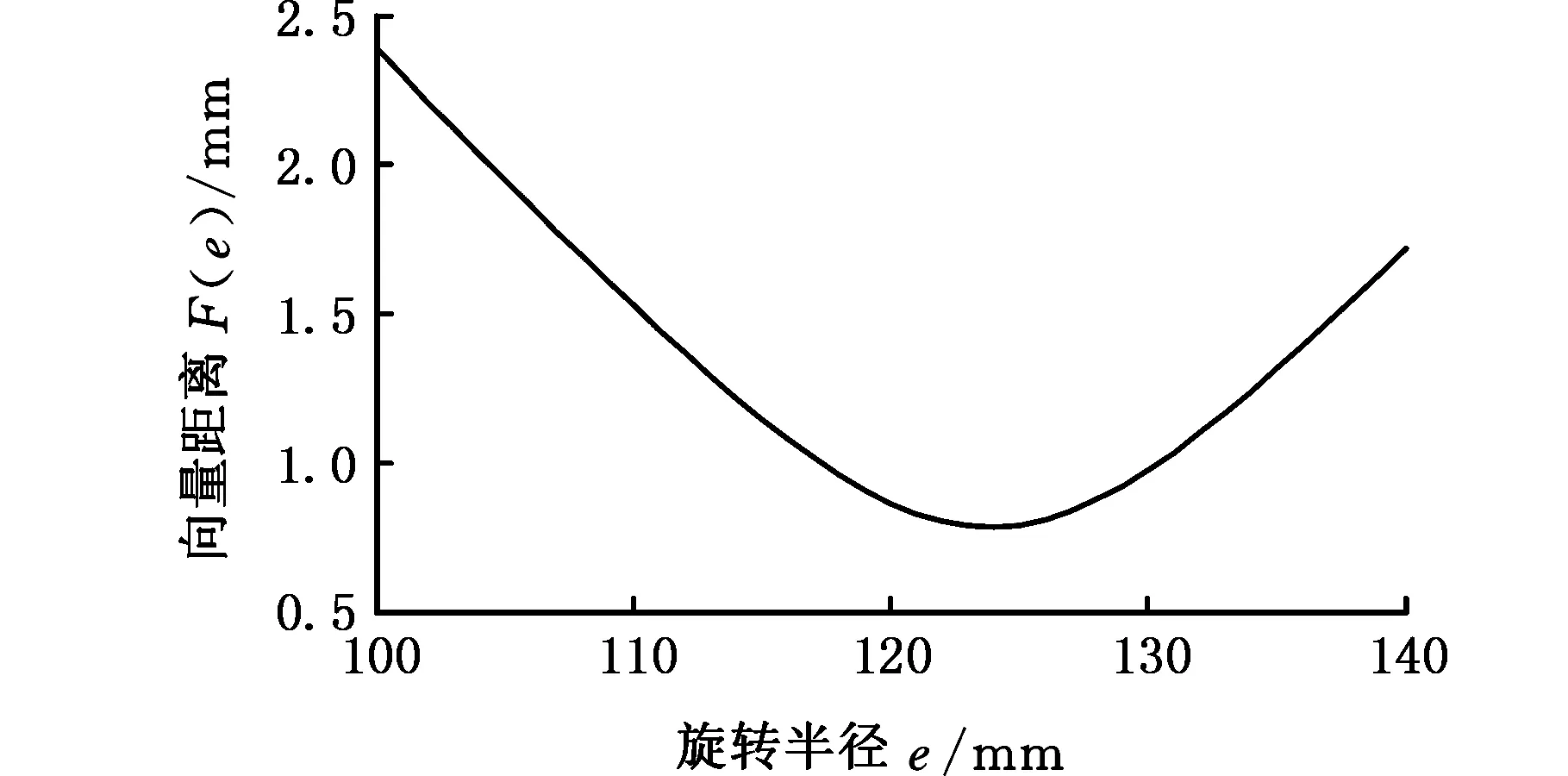
(b) m1=2 kg

(c) m1=4 kg图8 F(e)-e曲线Fig.8 The curve of F(e)-e

将旋转半径与实际情况相比较，若与实际差距较大，则适当调整偏心质量，重复上述步骤，以此确定合适的偏心质量和旋转半径，结果如表5所示。

表5 修正后数学模型在各组工况下的偏心质量和旋转半径

3.2 仿真与实验对比分析

上配重并入筒体的数学模型为未改进模型，本文新建立的数学模型为改进后模型，对这两种模型进行数值仿真，得到各工况下测量点的稳态响应。将仿真得到的每组工况下测量点振幅平均值随转速变化的趋势与实验结果进行对比，如图9～图11所示。将改进后数学模型在各工况下的测量点运动轨迹与实验结果进行对比，如图12所示。

(a)未改进

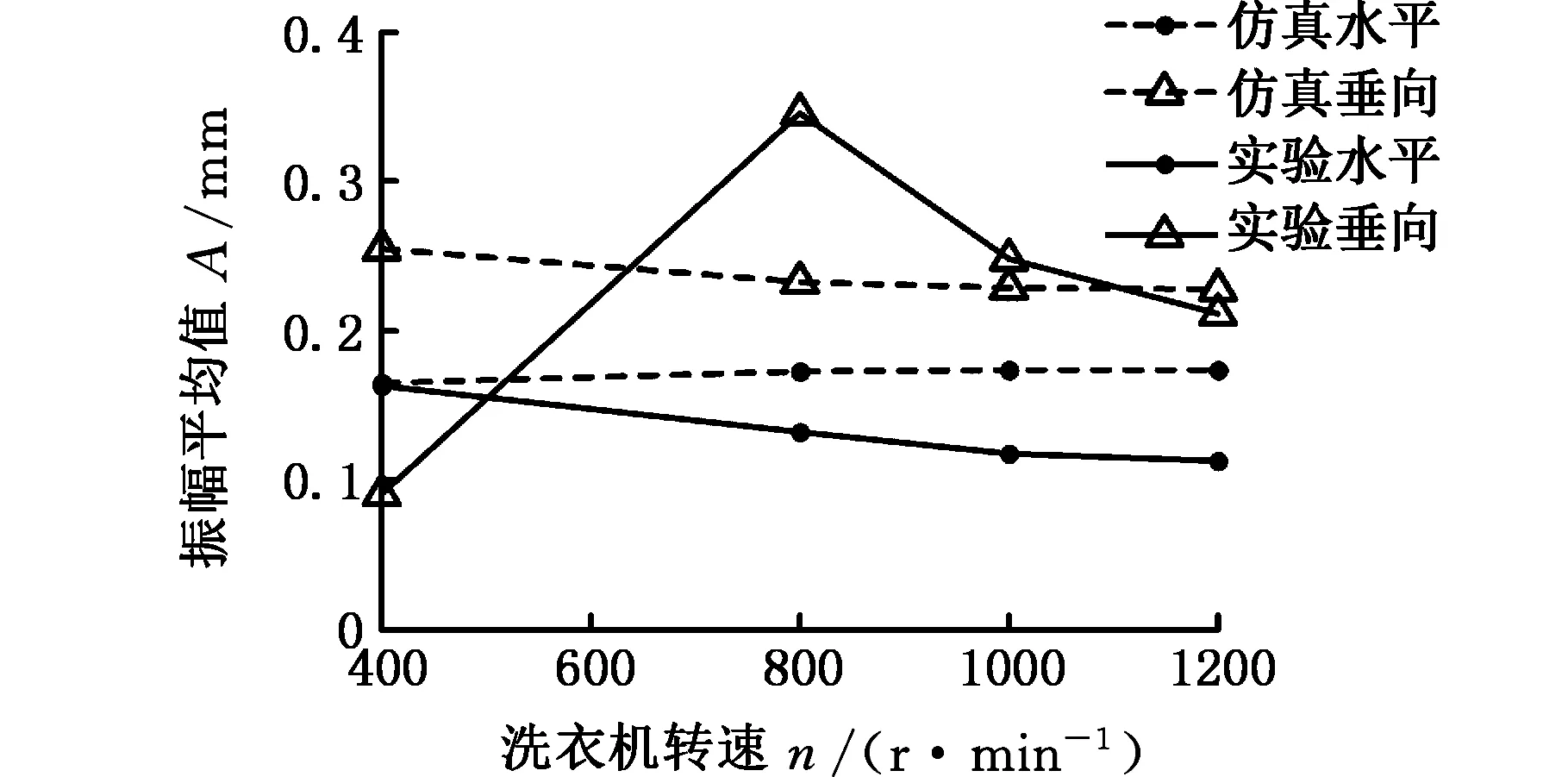
(b)改进后图9 m1=0时仿真与实验结果Fig.9 Simulation results and real measurements comparison under m1=0

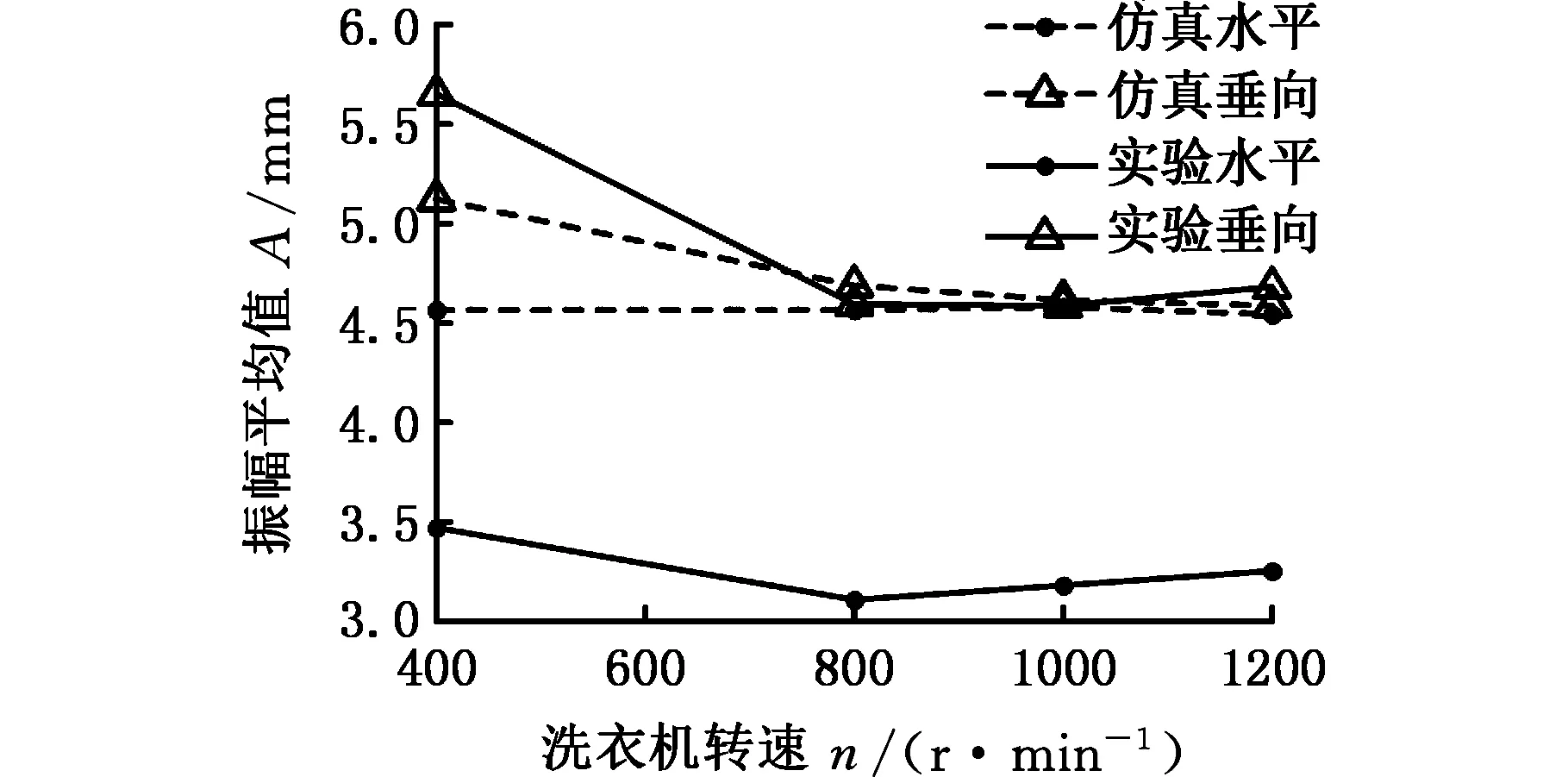
(a)未改进

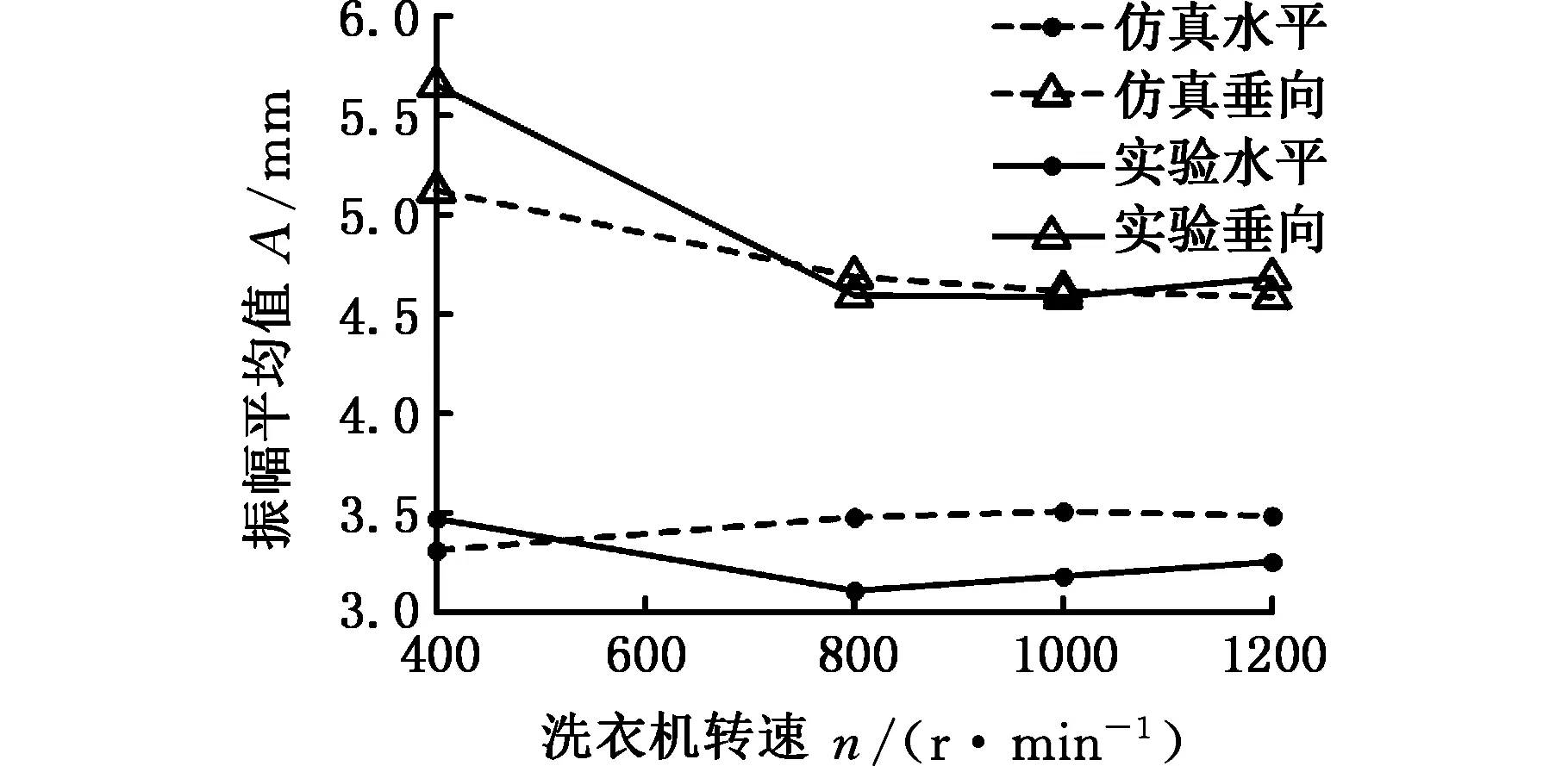
(b)改进后图10 m1=2 kg时仿真与实验结果Fig.10 Simulation results and real measurements comparison under m1=2 kg

综合图9～图11可知，是否独立考虑上配重对洗衣机筒体的垂向振幅无明显影响，而对筒体的水平振幅影响甚大。以往建模时上配重质量并入筒体，整个筒体质量均匀对称分布，此时筒体的水平振幅与垂向振幅数值相当接近，这种建模方式与仿真结果都与实际情况不相符。本文改进了建模方法，将上配重作为独立刚体，考虑其动能与势能，这样整个筒体的质量不再均匀分布，筒体水平与垂向振动不平衡这一特性得到更加准确的反映。

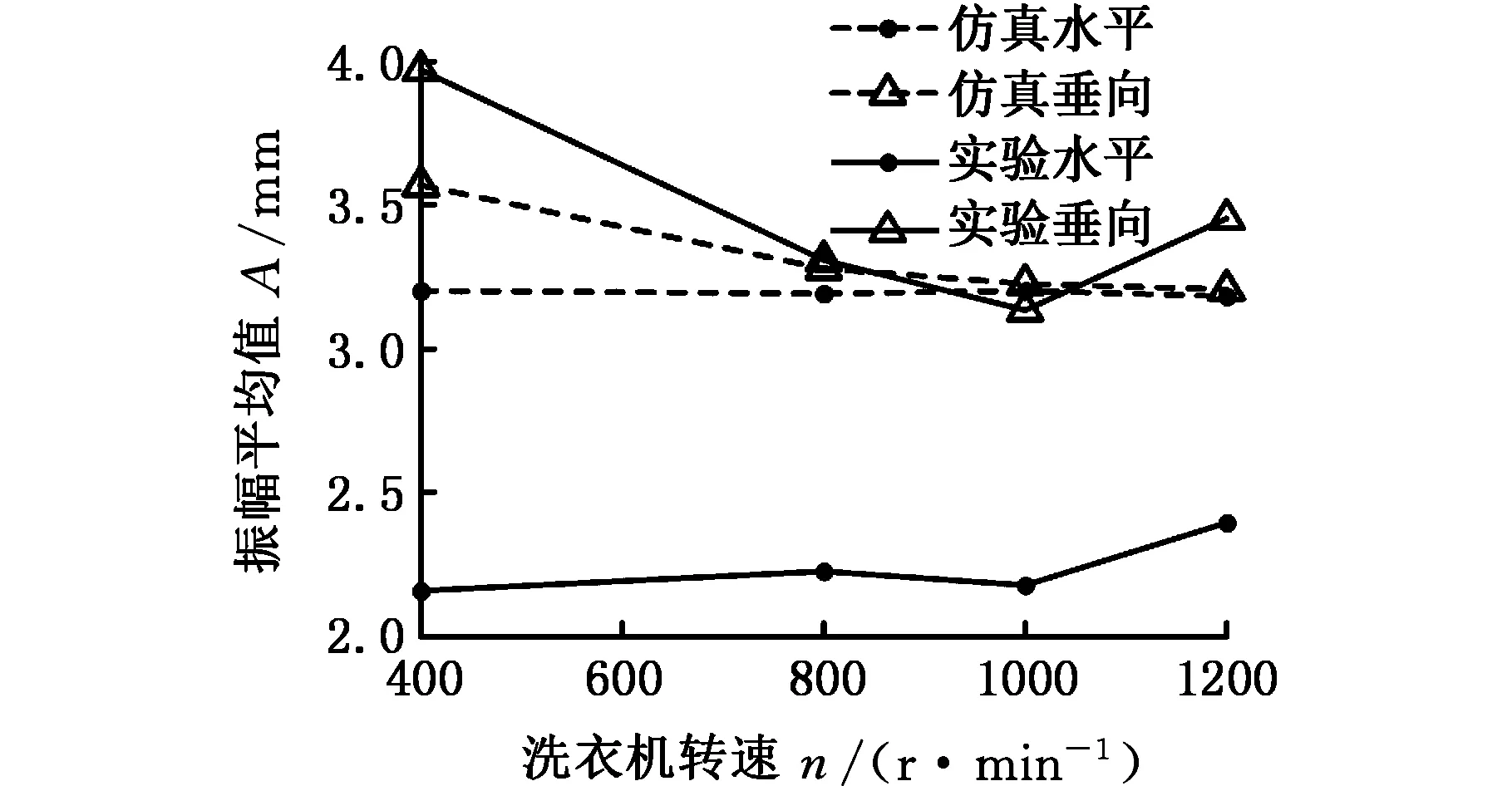
(a)未改进

(b)改进后图11 m1=4 kg时仿真与实验结果Fig.11 Simulation results and real measurements comparison under m1=4 kg

对比改进后的仿真与实验结果，可以发现，衣物质量为0时，两个结果的垂向振幅值及其随转速变化的趋势都存在较大误差，可能原因：一是此工况筒体振动微弱，测量误差较大；二是悬挂系统质量较小，各运动副阻力作用明显。由于此工况实际使用中不常出现，且筒体振动微弱，研究意义不大，所以不再纳入研究范围。

其他组工况下，仿真得到的振幅值随转速变化的趋势与实际测量基本一致。在400 r/min时筒体振动不稳定，此时垂向振幅最大，两结果的垂向振幅相对误差较大，最大达到13.71%。随着转速升高，筒体振动愈发稳定，垂向振幅逐渐减小，相对误差在2%左右。另外，整体上两结果在垂向振幅上的误差要小于水平振幅的误差。

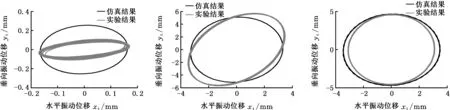
(a)Test01 (b)Test09 (c)Test10

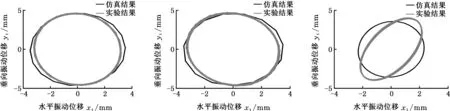
(d)Test11 (e)Test12 (f)Test17

(g)Test18 (h)Test19 (i)Test20图12 测量点轨迹对比图Fig.12 Comparisons of movement paths

结合图12分析，运动轨迹对比的结果进一步验证了上述观点。大部分工况下，测量点仿真运动轨迹与实验结果一致，说明随着输入工况的变化，数学模型的稳态响应与实际洗衣机的稳态响应一致，基于一系列假设建立的数学模型能够较准确地反映实际洗衣机的振动特性。

考虑到垂向振幅明显大于水平振幅，其对悬挂系统的振动影响更大，同时考虑部分结果误差较大，在使用本文建立的数学模型指导进一步减振研究时，侧重于将高转速下的筒体垂向振动作为研究对象。

4 结语

本文考虑洗衣机上配重对悬挂系统振动特性的影响，使用拉格朗日方程建立了滚筒洗衣机悬挂系统的数学模型。通过实验测量出洗衣机筒体上一点对脱水振动的稳态响应，以实验结果为目标对数学模型的参数进行了修正。在对数学模型仿真结果与实验结果进行对比分析后发现，本文建立的数学模型在参数修正后，能准确地反映多工况下的滚筒洗衣机的振动特性，可以指导滚筒洗衣机的减振研究。

[1] 付素芳，张秋菊，安伟.滚筒洗衣机悬挂系统动力学建模分析[J].机械设计与研究，2007，23(6):109-112. FU Sufang, ZHANG Qiuju, AN Wei. Dynamic Modeling and Analysis of Horizontal-axis Washing Machine Suspension System[J].Machine Design and Research,2007,23(6):109-112.

[2] 高建.滚筒洗衣机动态仿真及关键零部件优化[D].天津：天津大学，2008. GAO Jian. Dynamics Simulation of Front Loader Washing Machine and Optimization of Its Key Parts[D].Tianjin:Tianjin University,2008.

[3] 陈海卫，张秋菊.滚筒洗衣机瞬态脱水振动的分析与控制[J].振动与冲击，2013，32(15):47-53. CHEN Haiwei, ZHANG Qiuju. Transient Vibration Analysis and Control on a Horizontal Axis Washing Machine during Spin-drying Process[J]. Journal of Vibration and Shock, 2013,32(15):47-53.

[4] 范攀攀.滚筒式洗衣机动力学特性分析研究与参数优化[D].合肥：合肥工业大学，2012. FAN Panpan. The Research of Dynamic Characteristics and Parameters Optimization of the Drum Washing Machine[D].Hefei:Hefei University of Technology,2012.

[5] BOYRAZ P, GÜNDÜZ M. Dynamic Modeling of a Horizontal Washing Machine and Optimization of Vibration Characteristics using Genetic Algorithms[J]. Mechatronics, 2013, 23(6):581-593.

[6] 闻邦椿，刘树英，张纯宇.机械振动学[M].北京：冶金工业出版社，2010：57-58. WEN Bangchun, LIU Shuying, ZHANG Chunyu. Mechanical Vibration [M]. Beijing:Metallurgical Industry Press, 2010:57-58.

[7] 付素芳.滚筒洗衣机动态特性建模与结构参数优化研究[D].无锡：江南大学，2009. FU Sufang. Study on Dynamic Characteristics Modeling and Structural Parameter Optimization of a Drum Type Washing Machine[D].Wuxi:Jiangnan University,2009.

(编辑 王旻玥)

Dynamics Modeling and Experiments of Horizontal-axis Washing Machine Suspension System

WANG Hao LIU Lei

College of Mechanical and Electrical Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing，210016

Considering the effects of top balancing weights of washing machine suspension system, a dynamics model of this system was set up with Lagrange equations. Experiments were designed to measure vibrations of washing machine drum under multiple working conditions. An modification for parameters of dynamics model was performed based on the relation curves between the vibration amplitudes and speeds of the drum. The results calculated by dynamics model were compared with those obtained by experiments. The validity of dynamics model was verified.

washing machine; horizontal-axis; suspension system; top balancing weight; dynamics model; vibration measurement

2016-07-12

O327；O329；TP391.9

10.3969/j.issn.1004-132X.2017.11.009

王 豪，男，1991年生。南京航空航天大学机电学院硕士研究生。主要研究方向为滚筒洗衣机减振。刘 雷(通信作者)，男，1978年生。南京航空航天大学机电学院副教授。E-mail：liulei6278@163.com。