多层渐进黑白拓扑优化设计方法
付永清 张宪民
1.华南理工大学设计学院,广州,5106402.华南理工大学机械与汽车工程学院,广州,510640
多层渐进黑白拓扑优化设计方法
付永清1张宪民2
1.华南理工大学设计学院,广州,5106402.华南理工大学机械与汽车工程学院,广州,510640
提出一种多层渐进黑白(0-1)拓扑优化设计方法。采用SIMP方法松弛设计变量,利用灵敏度过滤消除棋盘格。将拓扑图中无效的中间单元看成多余材料,在此基础上,采用体积比多层延拓方案,逐步逼近优化问题的目标体积比,同时,利用基于相对密度的单元渐进筛选方法,分层地去除设计域中的无效材料,保留其中的最有效材料,并逐层缩小拓扑优化模型的可利用材料域。通过这种方式,使0-1拓扑设计转化为具有连续设计变量的多层渐进拓扑优化过程,从而最终得到满足目标体积比的黑白拓扑。最后,以柔性最小化及柔顺机构拓扑设计问题为例,进行了算法验证,结果表明该算法能够实现较好的0-1收敛效果。
黑白拓扑;优化设计;SIMP;多层;渐进
0 引言
目前,拓扑优化方法已经成为寻求经济又适用的拓扑结构形式的一种有效又实用的方法[1-2]。这种方法通常以有限元分析为基础,在拓扑优化的初始阶段,首先将设计域离散成一定数量的有限元网格,再利用优化算法确定单元材料的保留与删除,以满足预定的目标和约束条件。由于生产制造的原因,通常希望所得到的拓扑结果具有清晰匀质的黑白(0-1)设计模式。因而需要利用能够处理大量离散变量的整数规划方法,如遗传算法[3],模拟退火算法[4],渐进算法[5]等,寻找优化问题的可行解。但是,这类方法的不足之处在于计算量太大,并可能导致棋盘格或微穿孔现象出现。因此,为了减小求解过程中的困难,又发展了松弛法,如均匀化方法[6]和SIMP方法[7],以便可以采用基于连续变量的数学规划方法进行求解。其中,均匀化方法设计变量繁多,同时也可能产生棋盘格或微穿孔问题。而SIMP方法具有概念简单、计算效率高的特点,是目前拓扑优化领域应用最广泛的一种松弛方法[2]。不过,由于它的优化结果中容易出现灰色的中间单元(虽然通过增大该方法中惩罚因子的取值可以促使中间密度值趋近0和1,但较大的参数值同样将引起棋盘格的出现),因此在优化过程中还必须同时采用一些约束方法[2],以确保拓扑图中材料分布的连续性。然而由于这些约束方法又将导致拓扑图中容易出现灰色边界[2,8],因此,为了能够得到所期望的0-1拓扑,研究人员在松弛设计变量的基础上,又相继提出了一些解决中间单元问题的方法。如阈值法[9],在优化模型的目标函数[10]或约束条件[11]中追加显式惩罚函数方法,混合的SINH方法[12],修改最佳准则表达形式的启发式算法[13],二阶段方法[14],基于图像过滤技术的方法[15-16],单元连结参数化方法[17]和基于标准化元素的方法[18]等。从它们的优化结果来看,这些方法依然不能获得满意的0-1拓扑图。另外,还有基于曲线的方法,其中以水平集方法为代表[19],但这种方法也具有初始敏感性,不能生成新孔,以及难以收敛到不光滑的角点等缺陷。除了上述方法之外,还有模拟退火和SIMP相结合的方法[20],利用序列整数规划进行后处理的方法[21],以及基于复杂形状梁单元及图形理论的方法[22]等,这几种方法的共同之处是将松弛法和整数规划法相结合,因此也无法避免拓扑图中出现棋盘格或微穿孔现象,并且计算量较大。综上可知,解决中间单元问题的最佳方法仍有待研究。
因此,本文提出一种多层渐进黑白(0-1)拓扑优化设计方法。该方法采用SIMP方法松弛设计变量,利用灵敏度过滤消除棋盘格。算例验证结果表明,本文算法能够实现较好的0-1收敛效果。
1 多层渐进黑白拓扑优化方法
多层渐进方法的基本思想是,在将无效的中间单元看成多余材料的基础上,采用体积比多层延拓方案[23],逐步逼近优化问题的目标体积比,同时,利用基于相对密度的单元渐进筛选方法[23],分层地去除设计域中的无效材料,保留其中的最有效材料,并逐层缩小拓扑优化模型的可利用材料域,直至得到满足目标体积比的0-1拓扑。
1.1 体积比多层延拓方案
假定目标体积比为θ,初始阶段的拓扑优化层数为j=1,体积比为θ1,且θ1略大于θ,则体积比多层延拓方案可表示为
θj+1=max(αθj,θ)j≥1
(1)
其中,θj为第j层的体积比,α为体积比多层延拓因子,0 <α< 1,并且,在多层渐进拓扑优化过程中,α随层数j变化如下:
α=min(α0+(j-1)Δα,αu)
(2)
其中,αu为α的上限,以确保θJ-1及θJ(J为拓扑优化的总层数)精确取值为θ,α0为体积比延拓因子初值,且0<α0<1,Δα为体积约束延拓因子增量,且0<Δα<1。在实际应用中,为了确定α0和Δα的取值,需要首先给定总层数J的取值,另一方面,为了实现稳定的0-1收敛,第J层所需删除的单元数应为零,且第J-1层拟删除的单元数应尽可能地少。本研究中,选择第J-1层拟删除的单元数为1~5。
1.2 基于相对密度的单元渐进筛选方法
假定将设计域离散成N1个有限单元,{ρi}(i=1,2,…,N1)为第j层拓扑优化模型的最佳解,其中ρi为单元i的相对密度,且遵循SIMP松弛方法,因此任一ρi值满足:
0<ρmin≤ρi≤ρmax=1
(3)
式中,ρmin为单元密度下限,其作用是防止刚度矩阵奇异;ρmax为单元密度上限。
根据SIMP方法,ρi对优化问题的贡献可通过单元刚度矩阵Ki进行衡量[7],即
(4)
P∈Z,P>1,i=1,2,…,N1
式中,Ve为实心单元的材料体积;D为弹性矩阵;B为实心单元内任一点的应变矩阵;P为惩罚因子。
式(4)表明,和低密度单元相比,高密度单元对优化问题有更大的贡献,因而单元相对密度取值大小可作为单元渐进筛选依据,以删除设计域中的无效材料,保留其中的最有效材料。按从小到大的顺序对{ρi}进行重新排序,可得
(5)
i′=1,2,…,N1
然后从密度最小的单元开始,删除一定数量的低密度单元,直至设计域中所保留的单元数Nj+1等于第j层拓扑优化所期望的实心单元数,即有
(6)
式中,V0为设计域的总体积。
考虑到Nj+1为正整数,并且所删除的单元应为中间单元,将式(6)改写为[23]
(7)
其中,符号[·]表示取整运算。所有Nj+1个保留单元的集合构成第j+1层拓扑优化模型的可利用材料域Ωj+1,Ns是第j层优化解中密度为ρmax的单元数。由于第j+1层拓扑优化是在第j层拓扑优化最佳解的基础上进行的,因此,由Ns个密度为ρmax的单元构成的集合Ωj+1,2在下一层优化中恒定不变。
1.3 多层渐进黑白拓扑优化模型
综合多层渐进方法,可得优化问题第一层拓扑优化模型为
(8)
式中,K为整体刚度矩阵,且K=∑Ki;ρ为由ρi构成的列向量;f(ρ)为目标函数;F为仅在载荷输入点有非零元素Fin的力向量;U为Fin作用下的节点位移矢量;Fd为仅在位移输出点有非零单位虚拟载荷Fout的力向量;Ud为Fd作用下的节点位移矢量。
对于柔顺机构设计问题,为使其既有足够大的刚度又有足够大的柔性,可将f(ρ)表示为[14,24]
(9)
Es(ρ)=UTKU
(10)
(11)
式中,Es为系统的应变能[2];Ems为系统的互应变能。
当j≥2时,优化问题第j层拓扑优化模型为
(12)
式中,Ωj(j≥2)为优化模型的可利用材料域;Ωj,2为可利用材料域中密度为ρmax且恒定不变的单元集合;ΩjΩj,2为第j层优化模型可利用材料域中密度可变的单元集合;Ω1Ωj为第j层优化模型中所有已删除的单元集合。
2 多层渐进黑白拓扑优化最佳准则
结合传统的拓扑优化最佳准则[2]和多层渐进方法,可以得到第j+1层优化迭代中的密度更新准则为
(13)
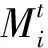
(14)

(15)
其中,∂f/∂ρi为目标函数的灵敏度,根据式(9)和式(10)可得[2,14,23-24]
(16)
(17)
此外,K(0)为实心单元的刚度,udi为单元i的虚拟位移,γ是拉格朗日乘子,可利用双截面算法调节,以使ρt+1满足体积约束,即[2,23,25]

(18)
3 灵敏度过滤
为了消除拓扑图中的棋盘格现象及确保拓扑优化解的存在性,采用灵敏度过滤算法对各单元灵敏度进行修正,即[2]
(19)
i=1,2,…,N1
其中,Ne为单元i的邻域, 该邻域内的各单元中心到单元i的中心的距离小于或等于过滤半径R,Hj是卷积因子,有[2]
Hj=R-‖xj-xi‖
(20)
式中,xi为单元i的中心坐标。
4 优化过程
多层渐近0-1拓扑优化过程如下:①建立第一层拓扑优化模型; ②对拓扑优化模型进行有限元分析,并得出体积约束和优化目标的灵敏度;③对优化目标的灵敏度进行过滤,以消除拓扑图中的棋盘格;④基于最佳准则更新设计变量;⑤重复步骤②~步骤④,直到优化迭代收敛;⑥判断拓扑优化最大迭代数或前后两次迭代的单元密度变化最大值小于一个阈值,或当前层删除单元数为零的条件是否满足,若满足则终止循环并输出结果,否则继续执行以下步骤;⑦建立下一层拓扑优化模型; ⑧重复步骤②~步骤⑦,如此不断缩小拓扑优化模型的可利用材料域,直至得到满足目标体积比的理想的柔顺机构0-1拓扑图。
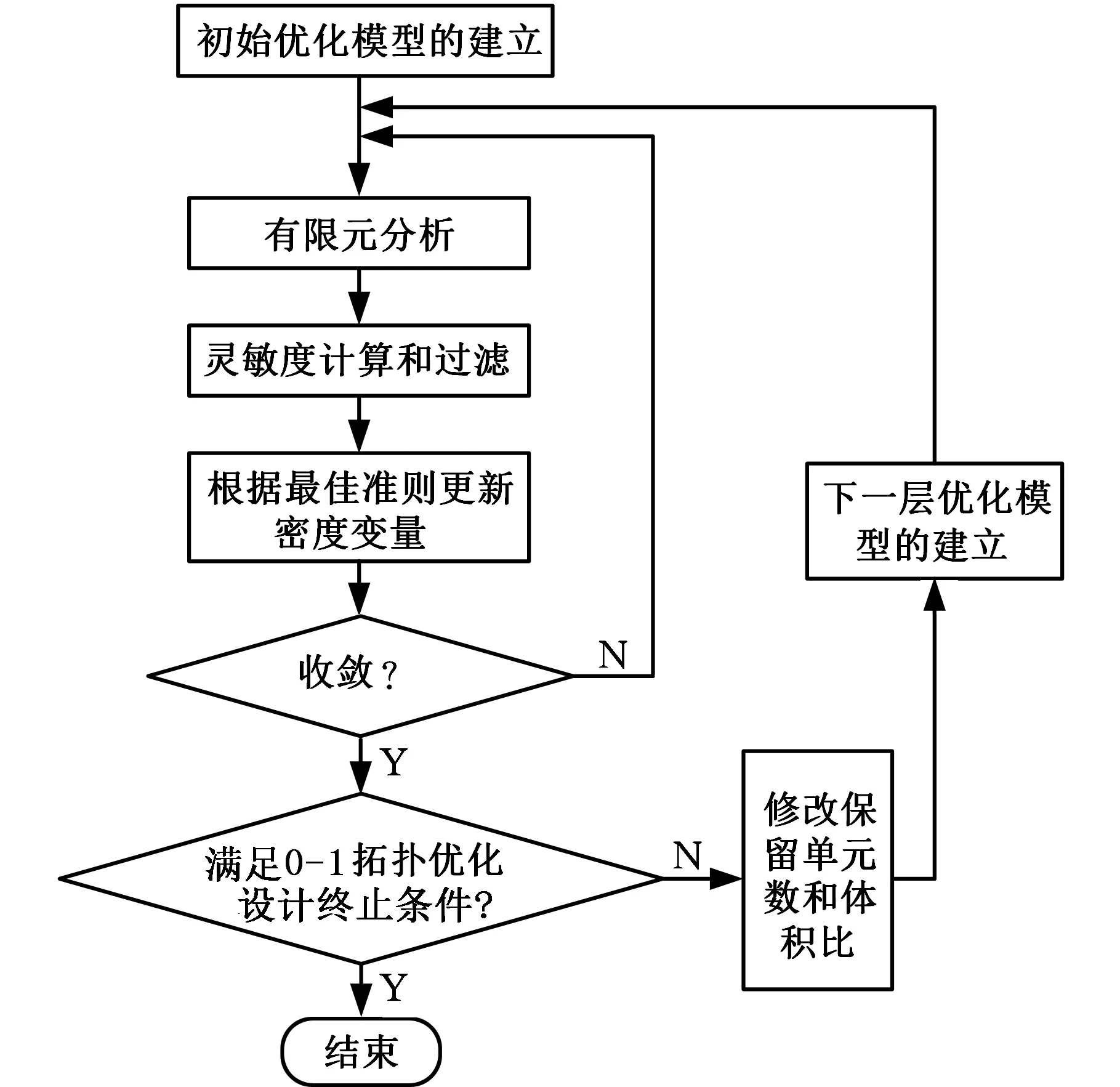
图1 多层渐进0-1拓扑优化设计流程图Fig.1 Flowchart of multi-level evolutionary approach for the 0-1 topology optimization design
图1为多层渐进0-1拓扑优化设计过程流程图。数值经验表明,设计问题的拓扑构成主要由第一层优化确定,因此,相较于后续各层来说,第一层优化迭代次数应选取更大的值。而且,在多层渐进方法中,多余的材料体积由待删除的中间单元构成,因此第一层拓扑优化的体积比只需取为稍大于目标体积比即可。另一方面,为了测量本文算法的0-1收敛效果,采用优化结果中的中间单元数N和非空单元的密度平均值ρa作为评价指标。其中,ρa定义为[16]
(21)
式中,Nn为优化结果中的非空单元数。
5 算例
5.1 MBB梁
图2所示为MBB梁设计域,大小为600 mm×100 mm,材料的弹性模量为210 GPa,泊松比为0.3,载荷Fin为10 N,目标体积比θ为0.5,过滤半径为0.15[16]。第一层的迭代次数取为100,后续各层的迭代次数取为20。拓扑优化方法采用相对密度法,惩罚因子设为3,优化目标是得到具有最小柔性的MBB梁的0-1最佳拓扑图。

图2 MBB梁设计域Fig.2 Design of MBB
优化问题采用四节点正方形单元进行求解,网格离散为180×30、240×40、300×50和360×60四种方式。首先采用传统最佳准则法求解拓扑优化问题,拓扑结果如图3所示。从图3中可以看出,优化结果中有明显的灰度区域,说明存在较多的中间单元。为此采用本文算法,在每一种离散方式中,对参数θ1、J、α0和Δα选取两组数值,如表1所示。其中,α0和Δα由θ1、J以及第J和第J-1层拟删除的单元数确定;选取α的上限值αu为0.998。最佳拓扑结果及数值解分别如图

(a)180×30网格 (b) 240×40网格

(c)300×50网格 (d) 360×60网格图3 基于传统最佳准则法的MBB梁最佳拓扑结果Fig.3 Optimal topology of MBB based ontriditional optimum criterion
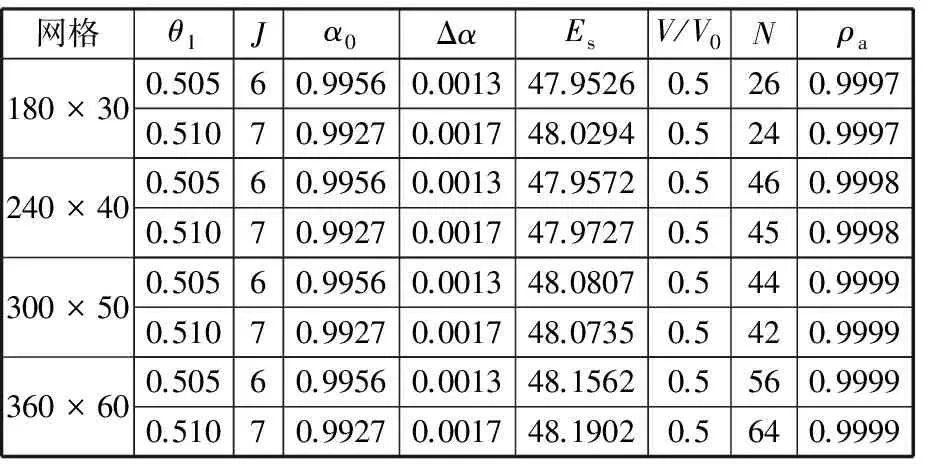
表1 多层渐进方法参数设置及数值解
4及表1所示。同时,目标函数和体积约束收敛过程分别如图5和图6所示。从图4可以看出,优化结果中没有出现明显的与中间密度值相关联的灰色区域,所有的拓扑图均具有清晰的黑白(0-1)设计模式。这是因为多层渐进方法将无效的中间单元看成多余材料,在此基础上,结合体积比多层延拓和基于相对密度的单元渐进筛选方法,分层地去除设计域中的无效材料,并保留其中的最有效材料,同时不断缩小拓扑优化模型的可利用材料域,因而随着优化层次的更新,拓扑图中的中间单元数不断减少,而实心单元数则不断增加,最终得到较满意的黑白拓扑。从图4还可看出,当参数θ1、J、α0和Δα变化时,无论网格密度是否变化,拓扑结果图均非常相似。这是由于在多层渐进方法中,MBB梁的拓扑构成主要由第一层优化确定,因而易于保证拓扑结果的恒定性。另外,从表1可见,所有的拓扑图均满足体积约束,且目标函数值相对恒定,虽然仍有少数中间单元存在,但其非空单元的密度平均值均以较高精度趋近于1,因而0-1收敛效果较好。再结合图5和图6可知,优化问题的目标函数和体积约束均能实现稳定的收敛。综上可见,本文算法对于柔性最小化问题的0-1拓扑设计是可行的。

(a)180×30,θ1=0. 505,J=6,α0=0.9956,Δα=0.0013

(b)180×30,θ1=0.510,J=7,α0=0.9927,Δα=0.0017

(c)240×40,θ1=0. 505,J=6,α0=0.9956,Δα=0.0013

(d)240×40,θ1=0.510,J=7,α0=0.9927,Δα=0.0017

(e)300×50,θ1=0. 505,J=6,α0=0.9956,Δα=0.0013

(f)300×50,θ1=0.510,J=7,α0=0.9927,Δα=0.0017

(g)360×60,θ1=0. 505,J=6,α0=0.9956,Δα=0.0013

(h)360×60,θ1=0.510,J=7,α0=0.9927,Δα=0.0017图4 MBB梁最佳拓扑结果Fig.4 Optimal topology of MBB
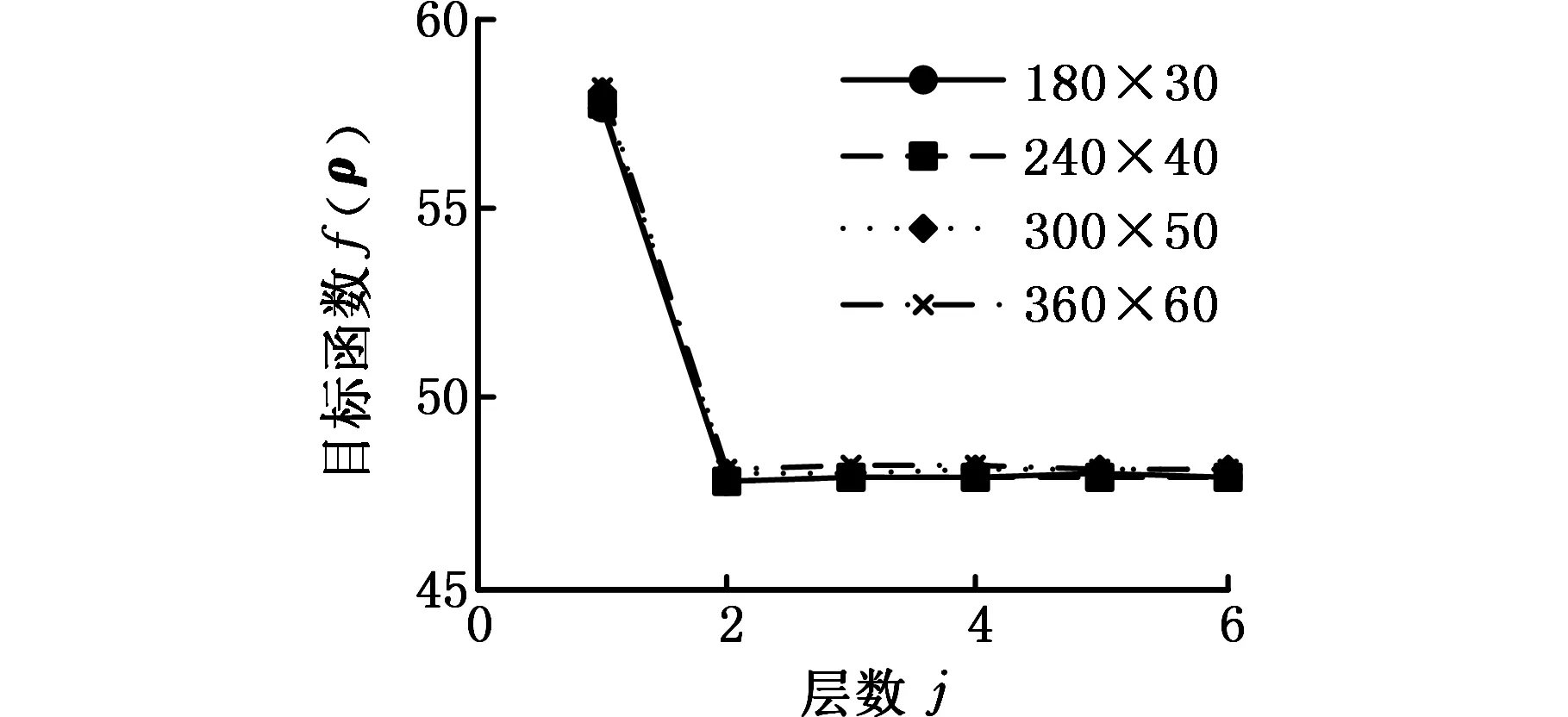
(a)θ1=0. 505,J=6,α0=0.9956,Δα=0.0013
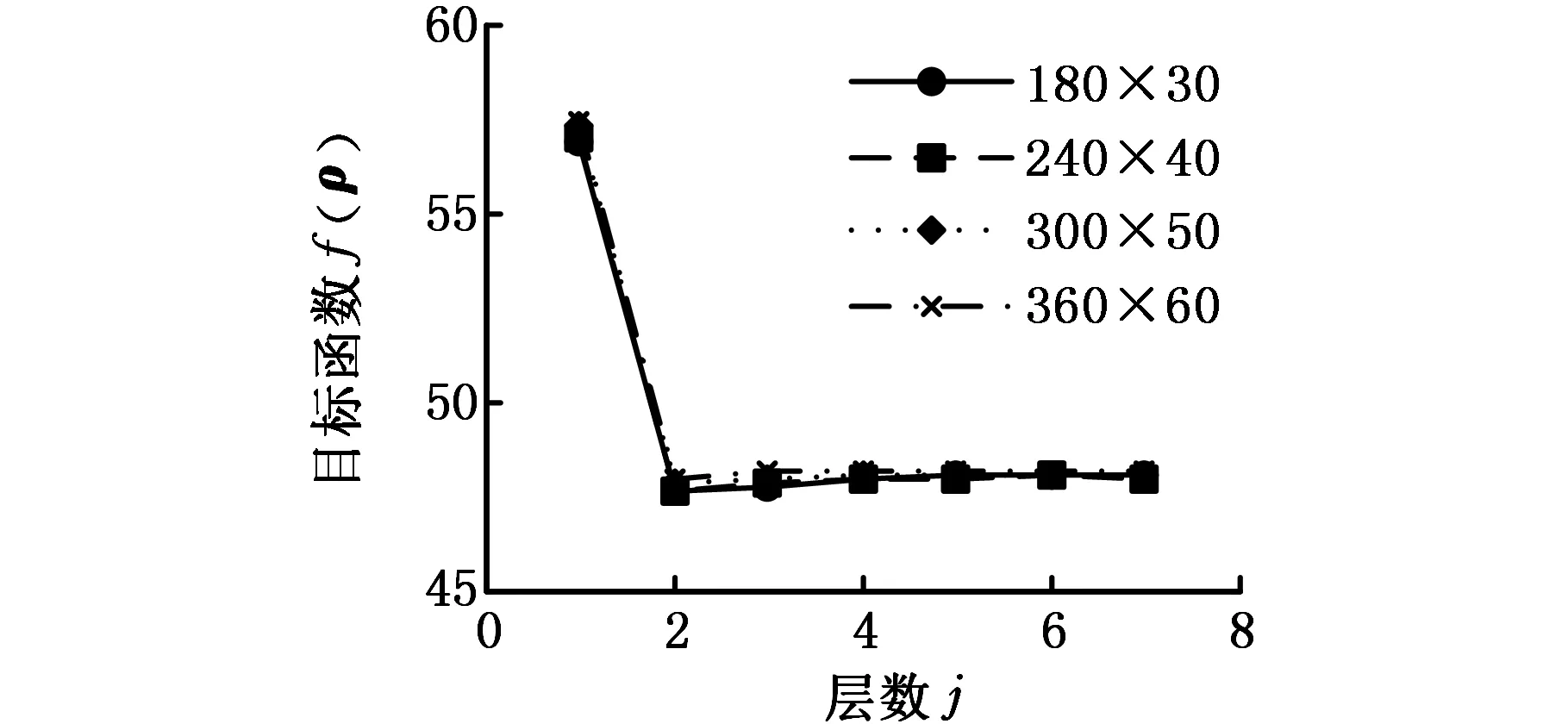
(b)θ1=0.510,J=7,α0=0.9927,Δα=0.0017图5 MBB梁目标函数收敛过程Fig.5 Converge process of objective of MBB
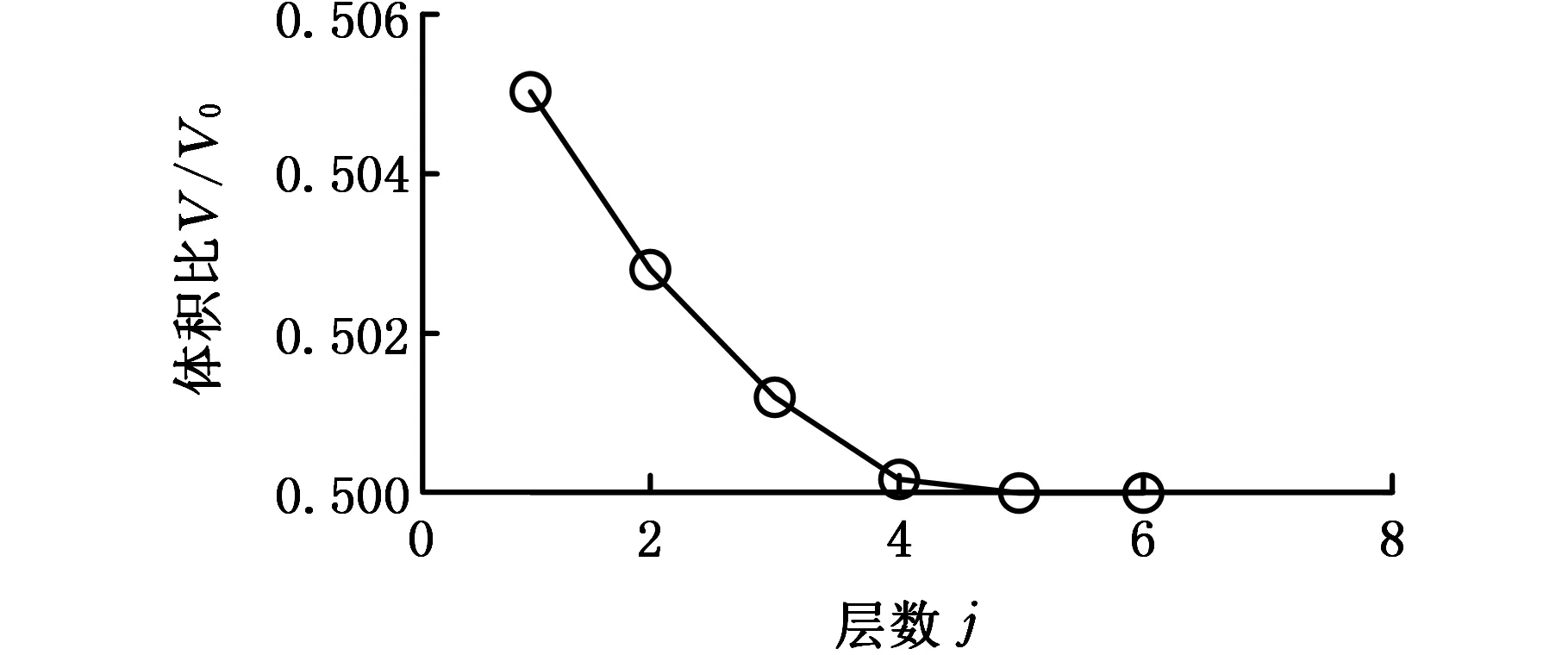
(a)θ1=0. 505,J=6,α0=0.9956,Δα=0.0013
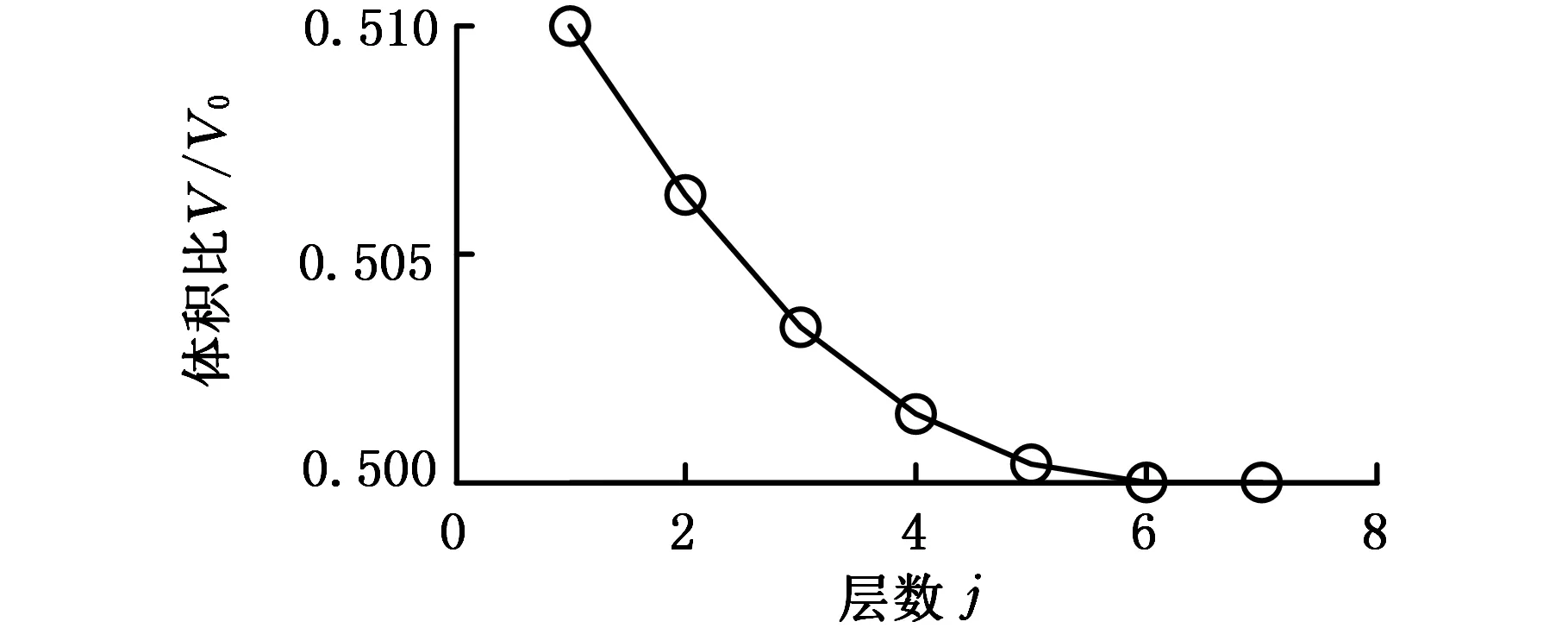
(b)θ1=0.510,J=7,α0=0.9927,Δα=0.0017图6 MBB梁体积约束收敛过程 Fig.6 Converge process of volume of MBB
5.2 柔顺力转换机构
图7所示为柔顺力转换机构设计域,大小为120 mm×120 mm,材料的弹性模量为210 GPa,泊松比为0.3,输入载荷Fin为10 N,目标体积约束比θ为0.25,过滤半径为2.5[15],输入输出弹簧刚度分别为1和0.001。此外,第一层的迭代次数取为300,后续各层的迭代次数取为20。由于对称性,仅对下半个设计域进行拓扑设计,拓扑优化方法仍采用相对密度法,惩罚因子设为3,优化目标是得到既有足够大刚度又有足够大柔性的柔顺机构0-1最佳拓扑图。
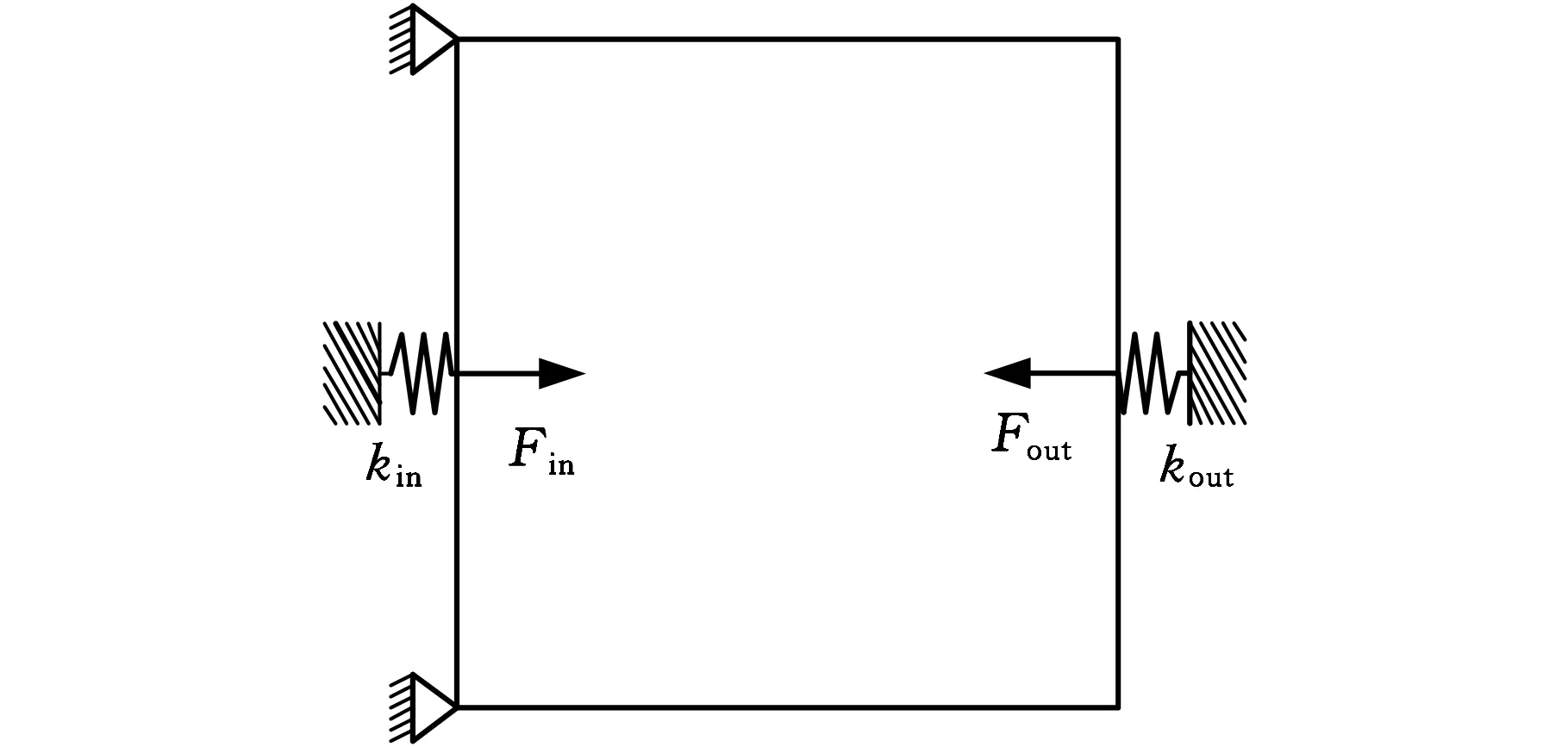
图7 柔顺力转换机构设计域Fig.7 Design of compliant force inverter
仍采用四节点正方形单元对优化问题进行求解,网格离散为120×60和180×90两种方式。首先采用传统最佳准则法求解拓扑优化问题,拓扑结果如图8所示。从图8中可以看出,优化结果中有明显的灰度区域,说明存在较多的中间单元。为此采用本文算法,在每一种离散方式中,分别对参数θ1、J、α0和Δα选取四组数值,如表2所示。其中,α0和Δα由θ1、J以及第J和第J-1层拟删除的单元数确定。并且,α的上限值αu仍取为0.998。最佳拓扑结果如图9和图10所示,相应的数值解如表2所示。另外,目标函数和体积约束收敛过程分别如图11和图12所示。由图9和图10可见,优化结果均为所期望的黑白(0-1)设计模式。无疑,这也是由于在多层渐进方法中,通过体积比多层延拓和单元渐进筛选相结合的方式,使拓扑图中的中间单元逐渐趋近0或1,从而得到较理想的黑白拓扑。同时,从这两个图还可看出,当参数θ1、J、α0和Δα变化时,拓扑结果图也都有较好的相似性。显然,这也是由于柔顺机构的拓扑构成主要取决于第一层优化的原因。另外,由表2可见,所有的拓扑图也都满足体积约束,且目标函数值也恒定,尽管仍存在少数中间单元,但其非空单元的密度平均值均以较高精度趋近或约等于1,因此同样具有较好的0-1收敛效果。结合图11和图12进一步可知,目标函数和体积约束都能稳定收敛。由上可知,本文算法对于柔顺机构问题的0-1拓扑设计是可行的。

(a)120×60 (b)180×90图8 基于传统最佳准则法的柔顺力转换机构梁最佳拓扑结果Fig.8 Optimal topology of compliant force inverter based ontriditional optimum criterion

表2 多层渐进方法参数设置及数值解

(a)θ1=0.260,J=6,α0=0.9816,Δα=0.0058

(b)θ1=0.260,J=7,α0=0.9854,Δα=0.0034

(c)θ1=0.265,J=6,α0=0.9722,Δα=0.0089

(d)θ1=0.265,J=7,α0=0.9779,Δα=0.0053图9 120×60网格柔顺力转换机构最佳拓扑结果Fig.9 Optimal topology of compliant force inverter with 120×60 mesh

(a)θ1=0.260,J=6,α0=0.9816,Δα=0.0058

(c)θ1=0.265,J=6,α0=0.9722,Δα=0.0089

(d)θ1=0.265,J=7,α0=0.9779,Δα=0.0053图10 180×90网格柔顺力转换机构最佳拓扑结果Fig. 10 Optimal topology of compliant force inverter with 180×90 mesh

(a)J=6
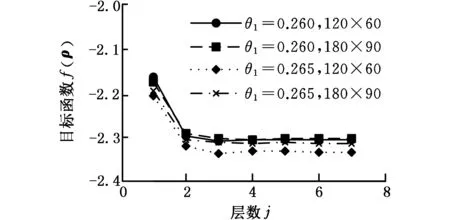
(b)J=7图11 柔顺力转换机构目标函数收敛过程Fig.11 Converge process of objective of compliant force inverter
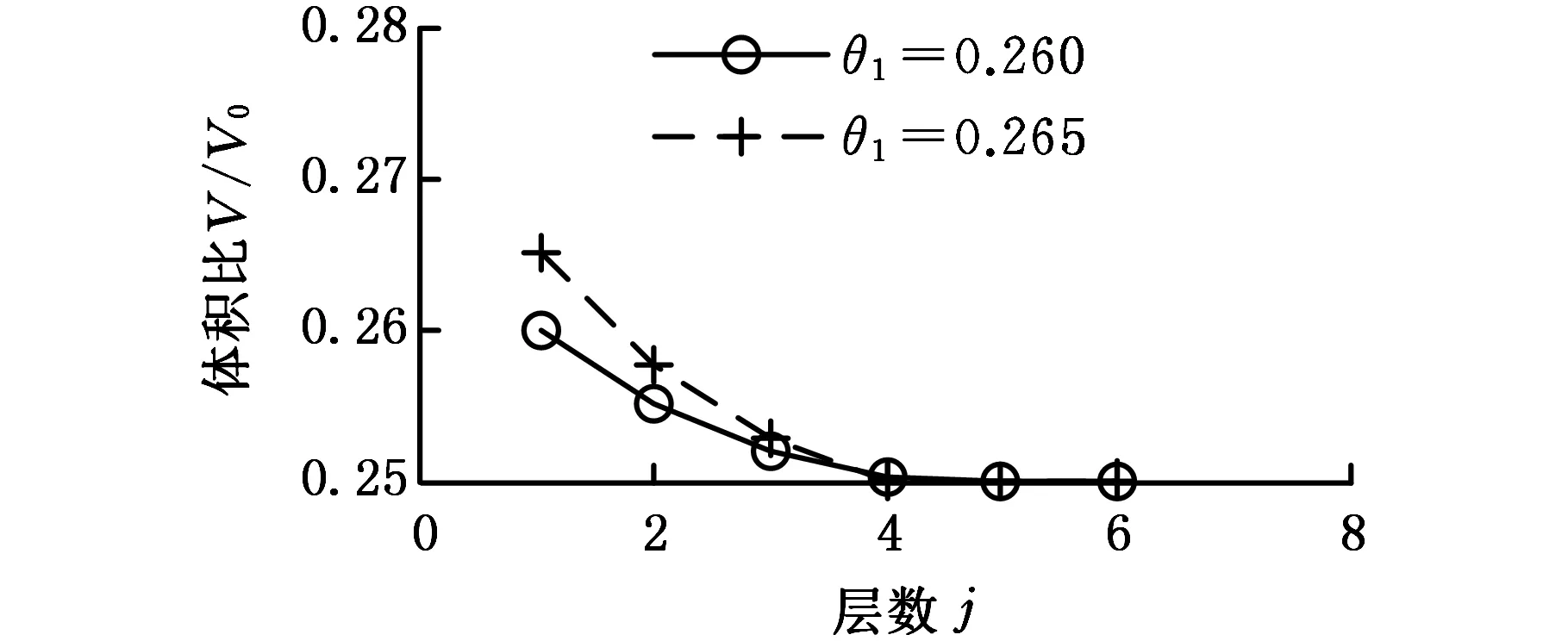
(a)J=6,120×60,180×90
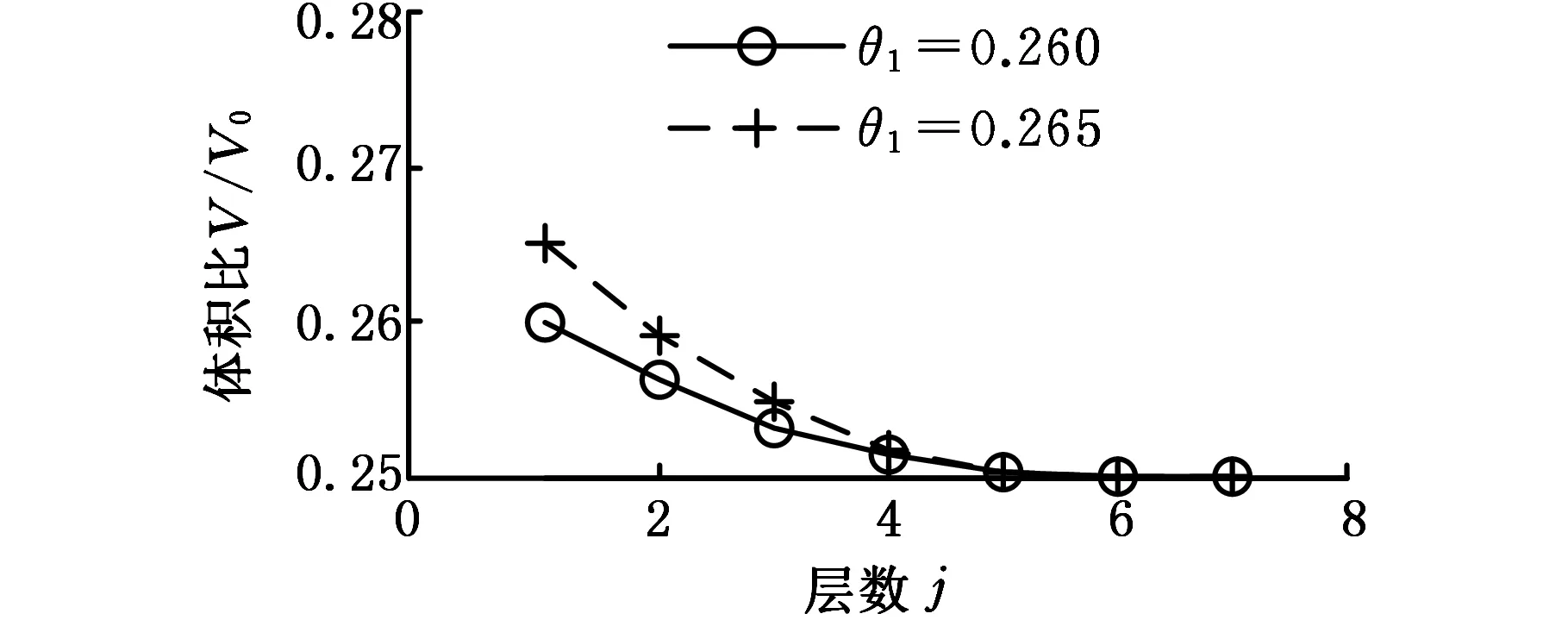
(b)J=7,120×60,180×90图12 柔顺力转换机构体积约束收敛过程Fig.12 Converge process of volume of compliant force inverter
[1] SIGMUND O, On the Design of Compliant Mechanisms Using Topology Optimization[J]. Mechanics of Structures and Machines,1997,25(4):493-524.
[2] BENDSØE M P, SIGMUND O. Topology Optimization: Theory, Methods, and Applications[M]. Berlin: Springer-Verlag, 2003.
[3] ANAGNOSTOU G, RHNQUIST E M, PATERA A T. A Computational Procedure for Part Design[J]. Computer Methods in Applied Mechanics and Engineering,1992,97:33-48.
[4] BUREERAT S, LIMTRAGOOL J. Performance Enhancement of Evolutionary Search for Structural Topology Optimisation[J]. Finite Elements in Analysis and Design,2006,42:547-66.
[5] HUANG X, XIE Y M. Convergent and Mesh-independent Solutions for the Bi-directional Evolutionary Structural Optimization Method[J]. Finite Elements in Analysis and Design,2007,43:1039-1049.
[6] NISHIWAKI S, FRECKER M I, MIN S, et al. Topology Optimization of Compliant Mechanisms Using the Homogenization Method[J]. International Journal for Numerical Methods in Engineering,1998,42:539-559.
[7] BENDSØE M P. Optimal Shape Design as a Material Distribution Problem[J]. Structural Optimization,1989,1:193-202.
[8] 付永清,张宪民. 结构及柔顺机构拓扑优化设计中的拓扑图提取[J]. 力学进展,2006,36(1):75-84. FU Yongqing,ZHANG Xianmin. Topology Extraction Process in the Topology Optimization Design for Structures and Compliant Mechanisms [J]. Advances in Mechanics,2006,36(1):75-84.
[9] KIKUCHI N, NISHIWAKI S, FONSECA J S O, et al. Design Optimization Method for Compliant Mechanisms and Material Microstructure[J]. Computer Methods in Applied Mechanics and Engineering,1998,151:401-417.
[10] LIN C Y, SHEU F M. Adaptive Volume Constraint Algorithm for Stress Limit-based Topology Optimization[J]. Computer-Aided Design,2009,41:685-694.
[11] BORRVALL T, PERTERSSON J. Topology Optimization Using Regularized Intermediate Density Control[J]. Computer Methods in Applied Mechanics and Engineering,2001,190:4911-4928.
[12] BRUNS T E. A Reevaluation of the SIMP Method with Filtering and an Alternative Formulation for Solid-void Topology Optimization[J]. Structural and Multidisciplinary Optimization,2005,30:428-436.
[13] GROENWOLD A A, ETMAN L F P. A Simple Heuristic for Gray-scale Suppression in Optimality Criterion-based Topology Optimization[J]. Structural and Multidisciplinary Optimization, 2009,DOI 10.1007/s00158-008-0337-1.
[14] FU Y,ZHANG X. An Optimization Approach for Black-and-white and Hinge-removal Topology Designs[J]. Journal of Mechanical Science and Technology, Accepted with revision.
[15] SIGMUND O. Morphology-based Black and White Filters for Topology Optimization. Structural and Multidisciplinary Optimization,2007,33:401-424.
[16] WANG M Y, WANG S. Bilateral Filtering for Structural Topology Optimization[J]. International Journal for Numerical Methods in Engineering,2005,63:1911-1938.
[17] YOON G H, KIM Y Y. Element Connectivity Parameterization for Topology Optimization of Geometrically Nonlinear Structures[J]. International Journal of Solids and Structures,2005,42:1983-2009.
[18] JANG G W, KIM M J, KIM Y Y. Design Optimization of Compliant Mechanisms Consisting of Standardized Elements[J]. ASME Journal of Mechanical Design,2009,131,121006-1-121006-8.
[19] LUO Z, TONG L Y, WANG M Y, et al. Shape and Topology Optimization of Compliant Mechanisms Using a Parameterization Level Set Method[J]. Journal of Computational Physics,2007,227:680-705.
[20] GARCIA-LOPEZ N P, SANCHEZ-SILVA M, MEDAGLIA A L, et al. A Hybrid Topology Optimization Methodology Combining Simulated Annealing and SIMP[J]. Computers & Structures,2011,89:1512-1522.
[21] WERME M. Using the Sequential Linear Integer Programming Method as a Post-processor for Stress-constrained Topology Optimization Problems[J]. International Journal for Numerical Methods in Engineering,2008,76:1544-1567.
[22] SAUTER M, KRESS G, GIGER M, et al. Complex-shaped Beam Element and Graph-based Optimization of Compliant Mechanisms[J]. Structural and Multidisciplinary Optimization,2008,36:429-442.
[23] 付永清,张宪民. 一种柔顺机构0-1拓扑图提取方法:ZL201210547407.7[P].2015-10-28. FU Yongqing,ZHANG Xianmin. A 0-1 Topology Extraction Approach for Compliant Mechanisms:ZL201210547407.7[P].2015-10-28.
[24] SAXENA A, ANANTHASURESH G K. An Optimality Criteria Approach for the Topology Synthesis of Compliant mechanisms[C]// Proceedings of DETC'98 1998 ASME Design Engineering Technical Conferences. Atlanta, Georgia,USA,1998:1-14.
[25] 左孔天.连续体结构拓扑优化理论与应用研究[D].武汉:华中科技大学,2004. ZUO Kongtian. Research of Theory and Application about Topology Optimization of Continuum Structure[D]. Wuhan: Huazhong University of Science and Technology,2004.
(编辑 王艳丽)
Multi-level Evolutionary approach for the Black-and-white Topology Optimization Design
FU Yongqing1ZHANG Xianmin2
1.School of Design,South China University of Technology, Guangzhou, 510640 2.School of Mechanical and Automotive Engineering,South China University of Technology, Guangzhou, 510640
A multi-level evolutionary method for the 0-1 topology optimization design was proposed. The binary constraints on design variables were relaxed based on the scheme of SIMP. And the checkerboards were filtered and removed by sensitivity. The ineffective intermediate elements were considered as redundant materials. Then, a multi-level continuation scheme on the volume ratio was used to approach the objective volume ratio of the optimization problem gradually. Meanwhile, based on relative densities an evolutionary screening strategy for elements was applied to remove ineffective materials in the design stratified, to remain the most effective materials, and to diminish the available material domains of topology optimization models with the changing layers. By this way, the 0-1 topology design was transformed into a multi-level evolutionary procedure of the topology optimization. Consequently, a preferable black-and-white topology satisfying the objective volume ratio could be obtained as expected. Finally, numerical examples of the topology design including compliance minimization and compliant mechanism problems were employed to verify the feasibility of the proposed method. The results demonstrate that the present method may achieve a relatively good 0-1 convergent effect.
black-and-white topology; optimization design; solid isotropic material with penalization; multi-level; evolutionary
2016-07-20
国家自然科学基金资助项目 (51275174)
TH112
10.3969/j.issn.1004-132X.2017.11.007
付永清,女,1968年生。华南理工大学设计学院副教授。主要研究方向为柔顺机构拓扑优化及拓扑图提取。张宪民,男,1964年生。华南理工大学机械与汽车工程学院教授、博士研究生导师。

