基于密度体积插值方法的结构拓扑优化

许小奎 郭宝峰 金 淼

燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004



基于密度体积插值方法的结构拓扑优化

许小奎 郭宝峰 金 淼

燕山大学先进锻压成形技术与科学教育部重点实验室，秦皇岛，066004

针对变密度法结构拓扑优化中灰度单元的控制问题，提出了一种密度体积插值方法。该方法构造的刚度与相对密度之间的线性关系保证了迭代中单元刚度变化的稳定性；构造体积与相对密度之间的惩罚关系以实现惩罚中间密度，同时更有利于在中间密度向两端逼近的同时降低灰度单元的数量。应用该插值方法对位移约束体积最小化问题进行求解，所得结果显示，增大惩罚程度，优化过程浮动较小，算法相对稳定。与应用SIMP方法和RAMP方法的优化结果相比较可知，在求解同一结构拓扑优化问题时，采用该方法且增大惩罚程度后的优化结果中灰度单元减少明显。

插值方法；变密度法；位移约束；拓扑优化

0 引言

自1988年BENDSOE等[1]提出用于求解连续体拓扑优化的均匀化方法以来，连续体结构拓扑优化一直是结构优化领域研究的热点。变密度法[2-5]是在均匀化方法的基础上发展形成的一种算法，该方法由于建模简单、易于求解等特点而得到了广泛应用[6-7]。

变密度法中常用的密度插值方法是密度刚度插值方法，其原理是通过构造相对密度与刚度之间的惩罚关系来达到消除中间密度的目的。典型的密度刚度插值方法有SIMP (solid isotropic microstructures with penalization)方法[2-3]和RAMP (rational approximation of material properties)方法[4]。由于优化计算是建立在结构有限元分析基础之上的，密度刚度惩罚函数的作用主要体现在结构有限元分析上，即优化计算是基于惩罚刚度后的有限元分析结果的，优化过程中相对密度变化时，单元刚度变化较大，导致算法稳定性差且易使优化落入局部最优解，因此必须控制密度刚度函数的惩罚程度。对于SIMP方法，惩罚因子取值范围一般为3～5[8]。然而限定惩罚程度带来的后果是，中间密度不能够得到更大程度的惩罚，导致优化结果会存在相当一部分灰度单元。

针对上述问题，本文提出了一种密度体积插值方法，并采用该方法求解了位移约束条件下的结构拓扑优化问题。

1 密度体积插值方法

密度体积插值方法中为实现对中间密度的惩罚，构造单元体积与相对密度之间的关系为

Vi=Vi0ω(ρi)

(1)

其中，ρi为相对密度；Vi0和Vi分别为实体单元和插值后单元的体积；ω(*)为体积惩罚函数，对中间密度单元的体积向上进行惩罚，映射到最小体积的优化中，即为对目标函数进行了惩罚。

惩罚函数ω可为指数型惩罚函数：

(2)

亦可为有理型惩罚函数：

(3)

其中，p和q分别为两种形式惩罚函数的惩罚因子。如图1所示，ω1中惩罚因子p取值越小,惩罚程度越大，ω2中惩罚因子q取值越大,惩罚程度越大。惩罚程度越大，越有利于中间密度向两端逼近及降低灰度单元的数量。

(a)ω1

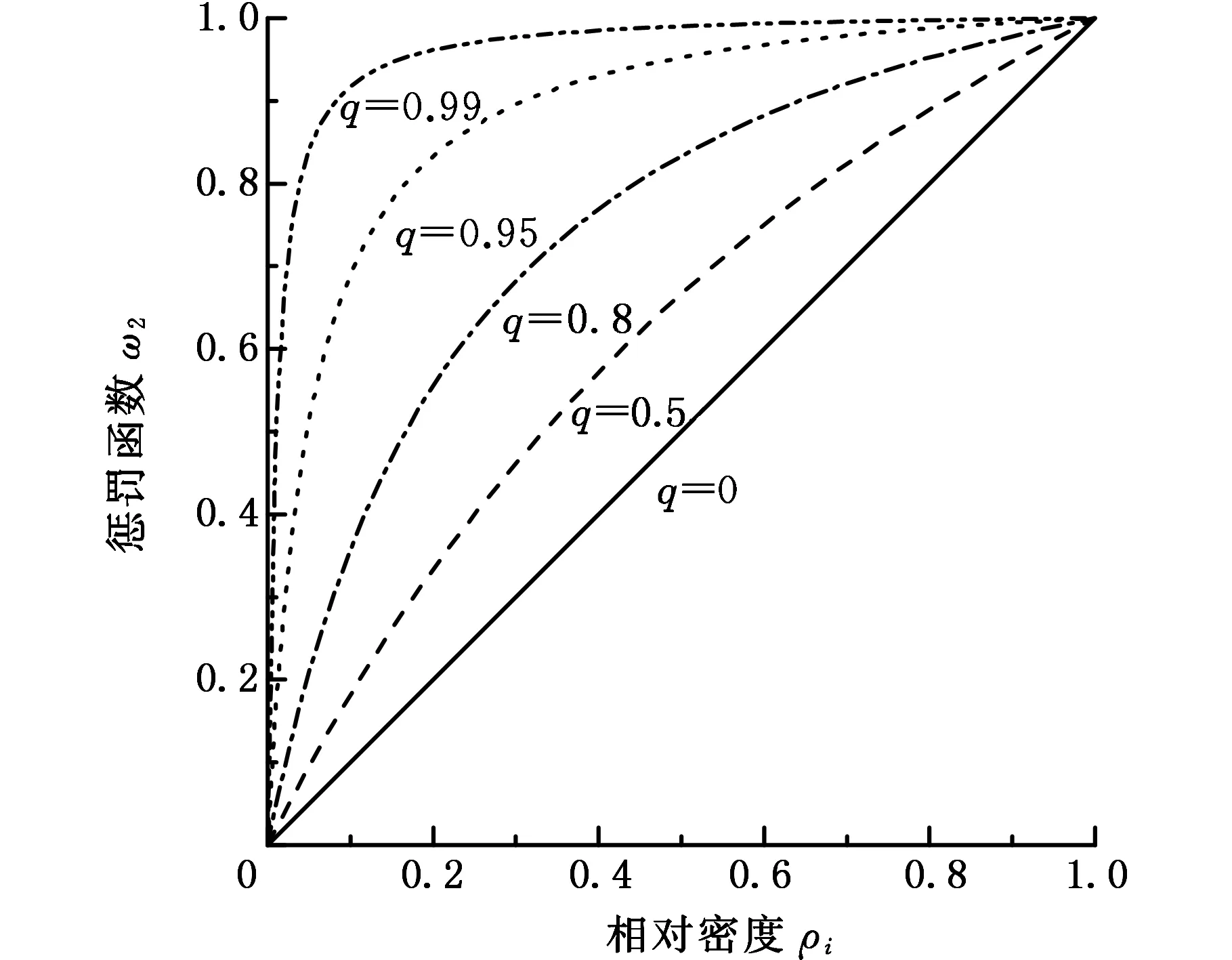
(b)ω2图1 ω函数惩罚曲线图Fig.1 The curves of penalty function ω

密度体积插值方法中，构造弹性模量与相对密度之间为线性函数：

Ei=ρiE0

(4)

式中，E0和Ei分别为实体单元和插值后单元的弹性模量。

这种线性关系即意味着单元刚度与相对密度之间为线性关系，反映在迭代过程中，便是单元刚度随相对密度稳定变化。

如果将密度体积插值方法中的中间密度材料看成是一种由空洞和实体材料组成的两相复合材料，则当实体材料的占比为ω时，由两相材料的Hashin-Shtrikman上下限[9]可知，体积模量κ和剪切模量μ需要满足：

(5)

(6)

(7)

(8)

式中，κ0和μ0分别为实体材料的体积模量和剪切模量；ν0为实体材料的泊松比。

将式(7)、式(8)代入到式(5)、式(6)，并且设定中间密度材料的泊松比与实体材料的一致，整理可得

(9)

(10)

将ω的两种形式(式(2)和式(3))代入到式(9)和式(10)，可以得到中间密度材料满足Hashin-Shtrikman上下限时，指数型和有理型惩罚函数中惩罚因子的取值范围:

(11)

(12)

当泊松比ν0取1/3时，可以得到

(13)

密度体积插值方法不同于密度刚度插值方法中通过弱化中间密度材料的刚度以惩罚中间密度，而是采用对体积进行惩罚，映射到体积最小化问题上，即通过对中间密度所对应的目标函数进行惩罚，以达到惩罚中间密度的目的。对比密度刚度插值方法和密度体积插值方法的优化迭代过程，对于相同的步长，即相同的相对密度变化，密度刚度插值方法因其刚度与相对密度呈惩罚关系而导致单元刚度变化剧烈且不稳定；密度体积插值方法中刚度与相对密度呈线性关系，因而单元刚度变化稳定。单元刚度变化的稳定关系着计算过程的稳定，所以密度体积插值方法具有更稳定的优化过程。

2 优化模型与求解策略

位移约束条件下求结构最小体积的优化问题可以表示为

(14)

由密度体积插值方法，可得体积敏度为

(15)

通过虚载荷法可以求解位移敏度为

(16)

式中，vUj和vuji分别为虚载荷法求解节点位移敏度时的虚载荷总位移矩阵和虚载荷单元位移矩阵；ki0为实体单元刚度矩阵；ui为第i个单元的位移向量；U为全局位移矩阵。

根据Kuhn-Tucher最优化条件，在最优解处满足：

(17)

式中，λj为拉格朗日乘子。

根据式(17)及设计变量上下限构造迭代公式如下：

(18)

其中，k为迭代次数，α为松弛因子，用来控制设计变量变化幅度，保证迭代稳定收敛，本文中取α为0.5。Mi的表达式为

(19)

当ω取式(2)中ω1时，可得到

(20)

当ω取式(3)中ω2时，可得到

(21)

迭代公式中的拉格朗日乘子λj可以通过对偶方法[10-11]进行求解。

为解决优化过程中常出现的棋盘格[12]问题，采用基于敏度的过滤技术[13]对位移敏度进行过滤处理。对于任意单元b，以其中心为圆心，以rmin为半径作圆，圆内单元参与单元b的过滤计算，过滤后敏度为

(22)

权重因子Hi为

Hi=rmin-dist(i,b) {i∈N|dist(i,b)≤rmin)}

(23)

其中，dist(i,b)为过滤范围内单元i和中心单元b的距离，N为过滤范围内单元的数量。过滤处理起到均化作用，可有效消除数值奇异现象，过滤半径rmin一般取单元尺寸的1～3倍。

3 数值算例及分析

3.1 算例1

如图2所示，设计域大小为80 mm×40 mm，厚度为1 mm，下端面左右两端固定，中间位置作用竖直向下载荷F，大小为1000 N。位移约束为载荷作用点竖直向下方向上的位移，大小为0.1 mm。材料的弹性模量E0=210 GPa，泊松比ν0=0.3，过滤半径rmin=2.5 mm，初始设计变量取1。图3a、图3c、图3e是基于指数型惩罚函数ω1的优化结果，惩罚因子p分别为0.3，0.2，0.1。图3b、图3d、图3f是基于有理型惩罚函数ω2的优化结果，惩罚因子q分别为0.7，0.8，0.9。图4所示为采用不同惩罚因子结构体积的变化过程。表1为算例1优化结果数据。

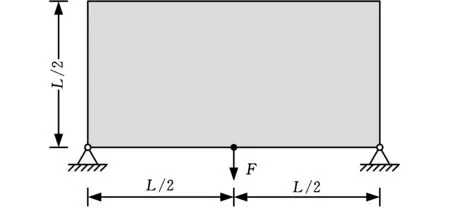
图2 算例1设计域和边界条件Fig.2 Design domain and boundary conditions for example 1

(a)p=0.3 (b)q=0.7

(c)p=0.2 (d)q=0.8

(e)p=0.1 (f)q=0.9图3 算例1优化结果Fig.3 Topology results for example 1

(a)指数型惩罚函数

(b)有理型惩罚函数图4 算例1体积变化过程Fig.4 Volume change process of example 1

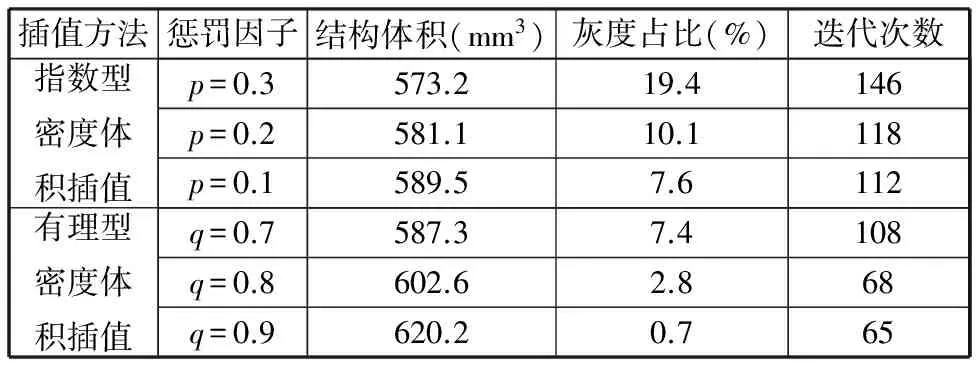
表1 算例1优化结果数据对比

从图3中的优化结果可以看出，基于指数型和有理型惩罚函数得到的优化结果拓扑形式一致。从图4可以看出，加大惩罚程度之后，迭代过程没有出现较大浮动，算法较稳定。从表1中数据可以看出，基于指数型密度体积插值方法的优化，随惩罚因子p的减小(即惩罚程度加大)，优化结果的体积小幅度增大，灰度单元减少，迭代次数减少。基于有理型密度体积插值方法的优化，随惩罚因子q的增大(即惩罚程度加大)，优化结果的体积小幅度增大，灰度单元减少，迭代次数减少。对比两种惩罚形式的迭代次数，可以发现有理型惩罚的迭代次数相对较少，在优化效率上占有优势。p=0.1和q=0.7时，优化结果的体积和灰度占比基本相同。

3.2 算例2

如图5所示，设计域大小为80 mm×40 mm，厚度为1 mm，下端面左端固定，右端竖直方向约束，A、B、C位置作用竖直向下的载荷F，大小为1000 N。位移约束为A、B、C三点竖直向下方向上的位移，大小都为0.15 mm。材料的弹性模量E0=210 GPa，泊松比ν0=0.3，过滤半径rmin=2.5 mm。图6a、图6b分别是基于本文密度体积插值方法的两种惩罚形式的优化结果。图6c、图6d分别是基于SIMP和RAMP插值方法的优化结果。表2所示为基于不同插值方法的优化结果数据对比。

图5 算例2设计域和边界条件Fig.5 Design domain and boundary conditions for example 2

(a)指数型密度体积 (b)有理型密度体积 插值方法 插值方法

(c)SIMP (d)RAMP图6 算例2优化结果Fig.6 Topology results for example 2

由图6可以看出，基于本文密度体积插值方法的优化结果与SIMP和RAMP方法的优化结果拓扑形式一致，而优化结果明显较清晰。从表2可以看出，本文密度体积插值方法的优化结果与SIMP和RAMP方法的优化结果相比，结构体积明显较小，且灰度单元较少。这是由于基于密度体积插值方法的优化中可以取得对中间密度更大程度的惩罚。

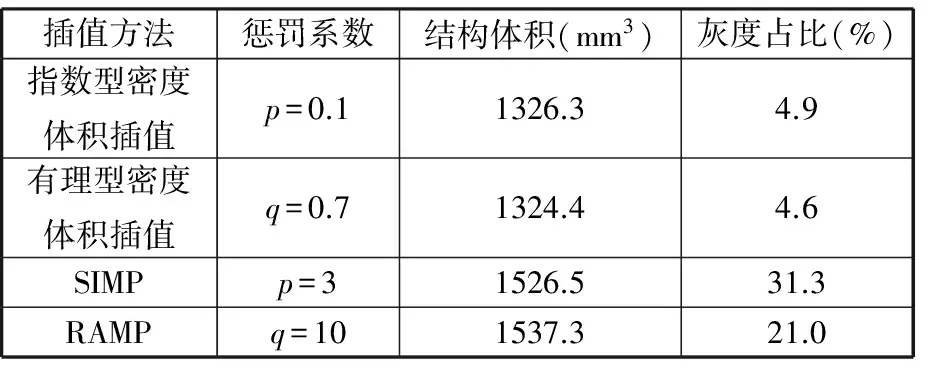
表2 算例2优化结果数据对比

4 结语

密度体积插值方法是通过构造单元体积与相对密度之间的惩罚关系实现惩罚中间密度的。该方法在位移约束求最小体积优化问题上的应用结果显示，随密度体积惩罚函数惩罚程度的增大，优化结果较SIMP和RAMP方法的灰度单元更少，且没有出现惩罚程度增大，优化不稳定甚至落入局部最优解等现象。

[1] BENDSOE M P, KIKUCHI N. Generating Optimal Topologies in Structural Design Using a Homogenization Method[J]. Computer Methods in Applied Mechanics and Engineering,1988,71(2):197-224.

[2] BENDSOE M P. Optimal Shape Design as a Material Distribution Problem[J]. Structural Optimization,1989,1(4):193-202.

[3] BENDSOE M P, Sigmund O. Material Interpolation Schemes in Topology Optimization[J]. Archive of Applied Mechanics,1999,69(9/10):635-654.

[4] STOLPE M, SVANBERG K. An Alternative Interpolation Scheme for Minimum Compliance Topology Optimization[J]. Structural and Multidisciplinary Optimization,2001,22(2):116-124.

[5] 罗震, 陈立平, 黄玉盈, 等. 连续体结构的拓扑优化设计[J]. 力学进展,2004,34(4):463-476. LUO Zhen, CHEN Liping, HUANG Yuying, et al. Topological Optimization Design for Continuum Structures[J]. Advances in Mechanics,2004,34(4):463-476.

[6] 杨陈, 郝志勇, 刘保林, 等. 变密度法在气缸体轻量化设计中的应用[J]. 浙江大学学报(工学版),2009,43(5):916-919. YANG Chen, HAO Zhiyong, LIU Baolin, et al. Application of Variable Density Method to Light-weight Design of Cylinder Block[J]. Journal of Zhejiang University (Engineering Science),2009,43(5):916-919.

[7] 朱剑峰, 林逸, 陈潇凯, 等. 汽车变速箱壳体结构拓扑优化设计[J]. 吉林大学学报(工学版),2013,43(3):584-589. ZHU Jianfeng, LIN Yi, CHEN Xiaokai, et al. Structural Topology Optimization Based Design of Automotive Transmission Housing Structure[J]. Journal of Jilin University (Engineering and Technology Edition),2013,43(3):584-589.

[8] 罗震, 陈立平, 钟毅芳. 基于凸规划方法的计算机辅助结构拓扑优化设计[J]. 计算机辅助设计与图形学学报,2005,17(4):774-781. LUO Zhen, CHEN Liping, ZHONG Yifang. Computer-aided Topology Optimization Using Convex Programming Method[J]. Journal of Computer-aided Design and Computer Graphics,2005,17(4):774-781.

[9] HASHIN Z, SHTRIKMAN S. A Variational Approach to the Theory of the Elastic Behaviour of Multiphase Materials[J]. Journal of the Mechanics and Physics of Solids,1963,11(2):127-140.

[10] BECKERS M. Topology Optimization Using a Dual Method with Discrete Variables[J]. Structural Optimization,1999,17(1):14-24.

[11] JOG C S. A Dual Algorithm for the Topology Optimization of Non-linear Elastic Structures[J]. International Journal for Numerical Methods in Engineering,2009,77(4):502-517.

[12] SIGMUND O, PETERSSON J. Numerical Instabilities in Topology Optimization: a Survey on Procedures Dealing with Checkerboards, Mesh-dependencies and Local Minima[J]. Structural Optimization,1998,16(1):68-75.

[13] SIGMUND O. Morphology-based Black and White Filters for Topology Optimization[J]. Structural and Multidisciplinary Optimization,2007,33(4):401-424.

(编辑 王艳丽)

Structural Topology Optimization Based on Density-volume Interpolation Scheme

XU Xiaokui GUO Baofeng JIN Miao

Key Laboratory of Advanced Forging & Stamping Technology and Science, Yanshan University, Qinhuangdao,Hebei,066004

A density-volume interpolation scheme applied in the variable density method was proposed, which was used for controlling grayscale elements in the topology optimization of continuum structures. In the new interpolation scheme, a linear relationship was established between the element stiffness and the relative density to ensure that the element stiffness changed smoothly with the changes of relative density in each iteration. And a penalty function was established between the element volume and the relative density in order to penalize the intermediate densities, which is better for reducing the number of grayscale elements acompained with the intermediate densities approaching both ends.The new interpolation scheme was introduced into the minimum volume optimization problems subjected to displacement constraints. The examples show that the optimization process changes little when increasing the penalty and it indicates that this algorithm is relatively stable. When solving the topology optimization problems with the same structures, it shows that there are less grayscale elements in the optimization results by using the new interpolation scheme than the results optimized by the SIMP and RAMP method. It is because a large penalty may be implemented on intermediate density in the new interpolation scheme.

interpolation scheme; variable density method; displacement constraint; topology optimization

2016-10-18

国家自然科学基金资助项目(51575474)；河北省自然科学基金资助项目(E2015203223)

TH122;O343

10.3969/j.issn.1004-132X.2017.11.003

许小奎，男，1990年生。燕山大学机械工程学院博士研究生。主要研究方向为成形设备结构分析与优化设计。E-mail:xxkysu@126.com。郭宝峰，男，1958年生。燕山大学机械工程学院教授、博士研究生导师。金 淼，男，1968年生。燕山大学机械工程学院教授、博士研究生导师。