飞机舵面液压助力器及舵面系统建模与性能仿真

陈 剑 邓支强 乔晋红

合肥工业大学噪声振动工程研究所，合肥，230009

飞机舵面液压助力器及舵面系统建模与性能仿真

陈 剑 邓支强 乔晋红

合肥工业大学噪声振动工程研究所，合肥，230009

以某型飞机飞行操纵系统典型液压助力器为研究对象，建立了液压助力器及舵面系统仿真分析模型。综合考虑油液刚度、结构刚度、摩擦、泄漏等非线性因素对系统的影响，推导出包含负载、活塞、缸体和阀芯动态的系统模型。针对助力器及舵面系统稳定性和静动态特性展开分析研究，阐述了关键参数对系统性能和稳定性的影响。仿真结果表明，该系统稳定性良好，响应迅速，具有良好的静动态性能。

液压助力器；飞行控制；稳定性；静动态特性

0 引言

飞行操纵控制系统中的液压助力器是飞行控制系统的重要组成部分，其性能的好坏及可靠性直接影响飞机和飞行控制系统的性能及安全[1-2]。液压助力器及控制舵面系统动态特性的研究，对于解决长期存在的飞机平尾抖动问题,提升新品种设计性能及保障飞行安全具有重要意义。

液压助力器属于机液位置伺服系统，是典型的非线性机液系统[3]。对此系统作总体考虑，先建立助力器及舵面系统的仿真模型，再根据实际的设计、样机、工作状况来构建系统模型，提高模型的精度,这样，一些复杂的因素如间隙、动静摩擦、阻尼和泄漏等因素就都可找到合适的解决方法[4]。

1 助力器及控制舵面建模

飞机舵面操纵系统使用的液压伺服作动器是一种机液位置伺服系统，由液压动力单元的闭合机械反馈机构构成反馈控制系统[3]。助力器主要由四边滑阀、对称液压缸及反馈机构组成，工作原理如图1所示。

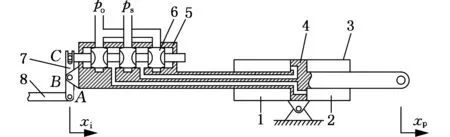
1.液压油腔1 2.液压油腔2 3.缸体 4.活塞 5.活塞杆壳体 6.阀芯 7.摇臂 8.拉杆图1 助力器原理图Fig.1 Principle diagram of hydraulic booster

无输入时，摇臂7处于垂直位置，阀芯6中立，阻断连接液压缸1腔、2腔的油路，活塞4位移被锁定。假设拉杆8对系统有一个向右的位移xi，此时活塞及活塞杆组件由于摩擦和惯性，并不产生运动，则摇臂7只能绕B点逆时针转动一定角度，于是滑阀阀芯便相对于活塞杆壳体5向左运动一定位移xv，从而打开液压缸1腔、2腔的油路。此时，1腔与进油路连通，2腔与回油路连通。在两腔液压油压力差的驱动下，活塞向右运动。此运动使摇臂7绕A点顺时针转动(外界输入停止，A点相当于固定点)，于是阀芯相对于活塞杆壳体向右运动使阀芯位移xv减小，直到阀芯再次将两腔油路阻断，阀芯回到中立位置，摇臂7重新转到垂直位置，活塞也相应停止不动。拉杆反向运动亦然，系统以此保持活塞输出位移xp与拉杆输入位移xi的一一对应。

液压助力器及舵面控制系统根据具体的反馈机构，布置形式有多种，现以典型的结构形式加以分析说明。图2所示为助力器及舵面控制系统模型和等效模型。图2中，Mp为活塞及杆惯量；Mc为缸体惯量；ML为等效惯性负载；KL为等效弹性负载；Kss为缸体支撑结构刚度；Kst为连接结构刚度；ps为额定工作压力；p0为额定回油压力；Bp为活塞黏性阻尼；BL为等效阻尼负载；Bss为缸体支撑结构阻尼；Bst为连接结构阻尼；xc为缸体位移；xL为负载位移；Cip为内泄漏系数;Cep为外泄漏系数;q1为流入1腔的流量;q2为流入2腔的流量;p1为1腔的油压压力;p2为2腔的油压压力。

(a)系统模型

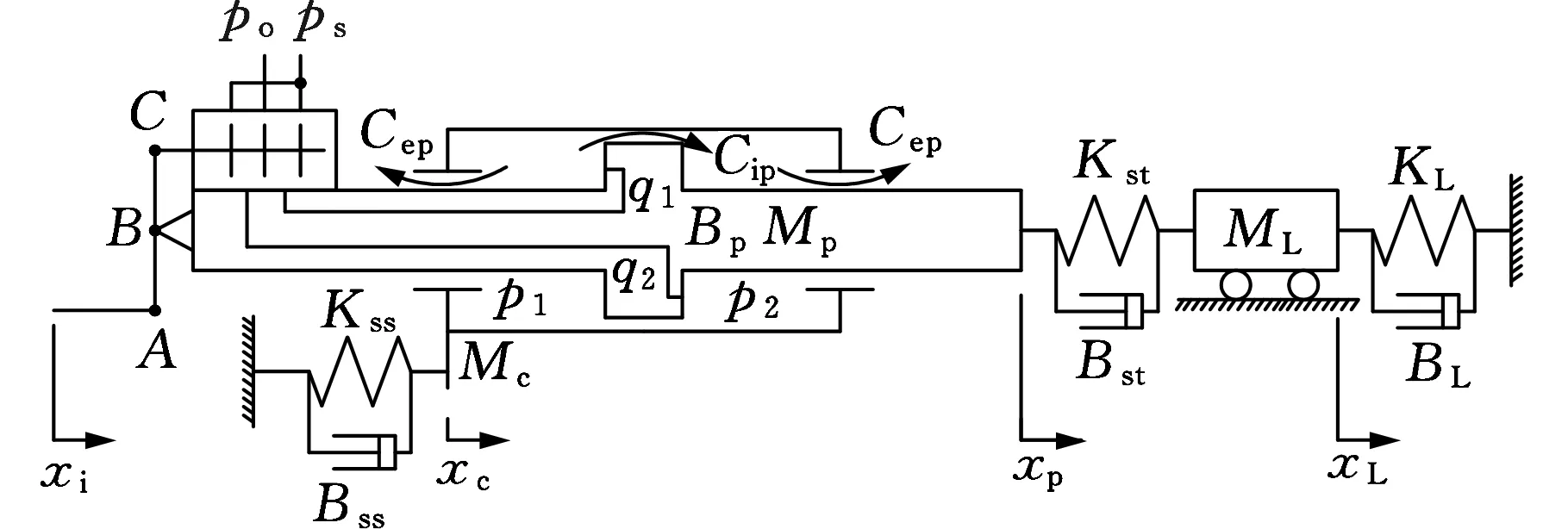
(b)等效模型图2 助力器及控制舵面模型Fig.2 Model of booster and rudder

1.1 滑阀模型

滑阀作为系统中的功率放大元件，其设计的合理与否对系统的性能有着决定性的影响[3]。为简化助力器常用的零开口四边滑阀反馈机构的建模，将摇臂部分的质量及阻尼折算到滑阀模型中，最终得到如下滑阀模型：

(1)

式中,Fi为驱动力；Mv为阀芯、阀腔流体及前置机构折算质量；Bv为阀芯/套黏性阻尼及反馈机构阻尼系数；Kf为稳态液动力刚度；FL为负载力。

由式(1)可知，在该子模型中需要设置惯量、阻尼、动静摩擦等主要参数以模拟阀芯的动态过程。稳态液动力的计算与阀芯凸肩工作边的形式及滑阀开口梯度有关，关系到滑阀的具体设计。阀口的流量特性要用液压元件阀芯阀套组合子模型来模拟。本文采用零开口四边滑阀，稳态液动力Fs=2CvCdW(ps-pf)xvcosθ=Kfxv[5]，其中，W为滑阀面积梯度；Cv为流速系数；Cd为流量系数；pf为负载压力；θ为滑阀节流口射流角。为保证流量与阀芯开度的线性关系，采用矩形过流窗口形式。在阀芯子模型中设置阀芯颈部直径、阀芯凸肩直径、开口梯度、阀芯工作边圆角半径和阀芯阀套间隙等设计参数，由此给定滑阀的流量特性：

当活塞正向运动(xv≥0)时,有

(2)

当活塞反向运动(xv<0)时,有

(3)

式中，ρ为油液密度。

1.2 反馈机构模型

由前文的工作原理可知，活塞的输出位移通过摇臂反馈给阀芯。在阀芯建模时已将摇臂的惯量折算到阀芯上，故此处不必再建立摇臂的动态模型，只需要表明反馈关系即可。系统的实时误差

e=KiRxi-KfRxp

(4)

式中,KiR、KfR分别为输入比与反馈比。

摇臂施加给阀芯的驱动力

Fi=(e-xv)Kr

(5)

式中，Kr为摇臂刚度；e-xv为阀芯实时误差。

由于将位移反馈改为力反馈，故需采用弹簧子模型模拟摇臂刚度，增益元件和比较元件表达反馈关系。

1.3 液压缸模型

助力器通常采用对称双杆结构保障双向运动一致性[6]。建模关键是要体现活塞及活塞杆组件和缸体的动态特性和流量连续性，它们分别由液压缸的动力参数和结构参数决定[7-9]。

1.3.1 活塞及活塞杆组件和缸体动态特性建模

活塞及活塞杆组件力平衡方程为

(6)

缸体力平衡方程为

(7)

式中，Ap为活塞有效面积。

由式(6)、式(7)可知，活塞及活塞杆组件和缸体的动态特性可以由其惯量、阻尼和刚度来表征，本文采用相应形式的质量块子模型及弹簧子模型完成动态特性建模。

1.3.2 液压缸流量连续性方程

对液压缸的流量特性进行精确建模需要考虑缸体的位移、油液的压缩性和液压缸的内外泄漏[10-11]。综合以上因素，液压缸流量连续性方程为

(8)

式中，Ey为有效油液弹性模量；V1、V2分别为液压油腔1、2的容积。

液压缸的流量特性主要由其结构设计参数决定，本文采用活塞子模型、泄漏子模型及可变容积子模型来完成建模。主要参数有活塞及活塞杆的直径、活塞宽度、活塞与缸体间的间隙和等效缸体体积弹性模量。

1.4 负载动态特性模型

负载主要有三类，即惯性负载、弹性负载和阻尼负载。在AMESim中，可用质量块子模型、弹簧子模型和阻尼子模型来模拟以上负载。负载力平衡方程为

(9)

由式(9)可知,根据惯量、阻尼和刚度，再结合前系统的连接刚度和阻尼即可以模拟负载部分的动态特性。

2 系统仿真

通过上述分析，结合助力器的具体结构形式，建立系统仿真模型,如图3所示。

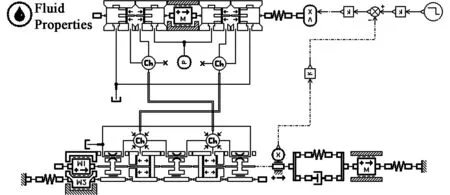
图3 助力器及舵面系统AMESim仿真模型Fig.3 AMESim simulation model of booster an rudder system

以某型液压助力器的结构参数和工作条件为基础构成本文模型的基本输入参数，主要参数如表1和表2所示。

表1 助力器参数Tab.1 Parameter of hydraulic booster

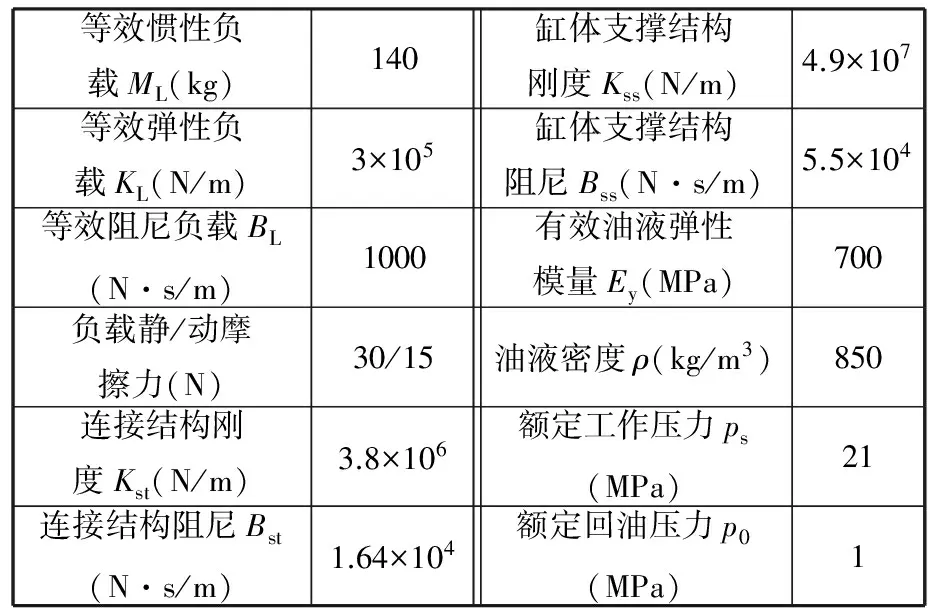
表2 外部参数Tab.2 External parameter

完成参数设置后进入仿真模式运行仿真。在进行分析时，需注意设置线性化时刻及控制变量和观测变量。

3 仿真结果与分析

3.1 关键参数分析

(1)滑阀面积梯度W与阀芯最大位移xvmax决定滑阀的最大流通面积，从而决定活塞的最大运动速度。面积梯度直接影响流量增益Kq，即决定了系统的开环放大系数和系统的响应时间常数。阀芯位移即为系统的跟随误差。在规定的最大运动速度下，面积梯度大时，系统响应迅速，跟随误差小，但稳定性差;面积梯度小时,则结果正好相反。W对活塞单位阶跃响应的影响如图4所示。这两个参数在系统快速性、准确性和稳定性方面需统筹考虑。

图4 不同面积梯度下活塞单位阶跃响应Fig.4 Piston unit step response under different area gradient

(2)系统位移反馈比KfR。该参数的存在使系统由开环变为闭环伺服控制，它对闭环系统的稳定性具有重要的影响。大的反馈系数使系统更加灵敏，但难以保证系统的稳定；而减小反馈系数，将减小反馈增益，增大跟踪误差。图5所示为反馈比对系统响应的影响。

图5 不同反馈比下活塞单位阶跃响应Fig.5 Piston unit step response under different feedback ratio

(3)系统中各处存在的阻尼是典型的软参数，对系统的稳定性有着重要的影响，通常需要根据经验或是实测数据来设定。如果设计有阻尼器，则可根据设计值来设定阻尼值。从图6中可以看出，增大阻尼能使系统变得更稳定，但会牺牲快速性能。

图6 不同阻尼下负载单位阶跃响应Fig.6 Load unit step response under different damping

3.2 时域响应与分析

阶跃幅值取阀芯最大开度值1 mm，在0 s处触发阶跃信号，仿真时间为0.2 s，通信间隔为0.0001 s，进行阶跃信号仿真，阶跃响应曲线如图7所示。由图7可知，活塞响应的建立时间为0.02 s，超调量为5%，调整时间为0.063 s，稳态误差为0.203 μm。负载响应的建立时间为0.017 s，超调量为21%，调整时间为0.113 s，稳态误差为55 μm。

图7 阶跃输入响应曲线Fig.7 Step inputresponse curve

阶跃响应曲线及各项指标表明，系统是稳定的，且响应迅速，动态过渡时间短，稳态误差较小。活塞的响应曲线是二阶振荡环节和一阶惯性环节的综合，说明该系统以三阶模型来表示将更加准确。活塞的动静摩擦、摇臂的刚度、阀芯的摩擦力及阀芯工作边的圆角大小都将影响活塞的稳态位移误差，但由响应曲线可知，该值已经十分微小，可以不考虑。负载的稳态位移曲线略低于1 mm的输入信号，是因为反馈取自活塞位移，由弹性负载引起的负载与活塞之间的相对位移未能进行校正。这一指标主要取决于助力器与舵面之间传动机构的静刚度，提高刚度可以减小位移误差。

图8所示为系统内部各变量的动态响应曲线。从图8中可以直观地观察阶跃响应时阀芯开度的最大值，以及动态变化过程，同时也可以查看负载流量、活塞速度和负载速度的动态过程，并进行必要的定性或定量分析。对部分参数进行调整后，流量和速度曲线都趋向于平滑，表明系统内部动态平稳，活塞和缸体的固有频率并没有影响系统动态的平稳性，仍然以负载的动态特性为主。

图8 阶跃输入系统内部动态曲线Fig.8 System internal dynamic curve under step input

液压缸两腔的压力动态过程如图9所示，两腔的压力值为对称变化，且变化平稳，没有出现高频的振荡现象。压力波动的最大幅值为0.6 MPa(6bar)，达到稳态的时间为0.07 s，稳态压差与弹性负载力平衡。只有在系统输出为0时，稳态压差才为0。

图9 阶跃输入两腔压力动态曲线Fig.9 Two cavity dynamic pressure curve under step input

3.3 频率响应与分析

对系统进行线性化分析，可以得到系统的频率响应曲线。图10为系统的开环伯德图和闭环伯德图。从开环伯德图中可以看出，系统的幅值裕度为21.85 dB,大于6 dB，相位裕度为80.66°，大于45°，说明系统具有良好的稳定性。从闭环伯德图可以看出，在输入为1 Hz时，输出相位滞后为5.69°，在工作频段内具有很好的相位跟随性。闭环截止频率为11 Hz，远大于最大工作频率，系统工作带宽满足要求。

(a)开环伯德图

(b)闭环伯德图图10 系统伯德图Fig.10 Bode diagram

系统的特征根为S1=-63.5，S2=-38.6±14.5j，S3=-1516.8±2072.5 j,S4=-1149.7±4436.8 j。可知所有的极点都位于虚轴的左侧，S3和S4离虚轴较远，对系统的影响较小。系统相应的过渡过程主要由阀控缸部分的闭环极点引起的暂态分量决定[12]。结合图7阶跃响应曲线可知，系统的响应速度快，存在振荡，有些超调。S1离S2相对较近，负实数极点对应的暂态分量将对过渡过程有一定的影响，这与阶跃响应曲线反应出的结果基本一致。

4 结论

(1)系统的稳定性对关键参数的设计十分敏感，滑阀面积梯度W大，则开环增益大，响应迅速，跟随误差小，但系统稳定性差，反之则结果正好相反。反馈比KfR体现了系统快速性和稳定性的矛盾，增大反馈比能使系统反应敏捷，而稳定性和动态品质将变差。各处结构阻尼对保证系统稳定具有重要作用，然而无法精确确定，是仿真分析需要重点关注的参数。

(2)通过增加摇臂刚度Kr，提出阀芯实时误差(e-xv)这一概念，将系统闭环由位置反馈转变为力反馈，从而建立阀芯的动态模型，考察阀芯动态对系统性能的影响，同时也为进一步的研究提供了新的思路。

(3)分别建立活塞及活塞杆组件和缸体的动态模型，独立分析活塞及活塞杆组件和缸体响应特性，以及其对负载(舵面)响应的影响。

(4)仿真结果表明仿真模型能够准确地对系统的动态特性进行预测，阶跃响应与频响曲线都表明系统是稳定的，从系统内部变量的动态过程可以看出，系统具有良好的动态过渡特性。

[1] 王永熙.飞机飞行控制液压伺服作动器[M].北京：航空工业出版社,2014:1-2. WANG Yongxi. Aircraft Flight Control Hydraulic Servo Actuator[M]. Beijing： Aviation Industry Press,2014:1-2.

[2] 郭辉,王平军,郭涛.基于Simulink的飞机液压助力器建模与仿真研究[J].机床与液压,2007,35(9):222-223. GUO Hui，WANG Pingjun，GUO Tao. Modeling and Simulation for Hydraulic Booster Based on Simulink[J].Machine Tool & Hydraulics,2007,35(9):222-223.

[3] 王春行.液压伺服控制系统[M].北京：机械工业出版社,1989:96-97. WANG Chunxing. Hydraulic Servo Control System[M]. Beijing: Mechanical Industry Press,1989:96-97.

[4] 郭军,吴亚峰,储妮晟.AMESim仿真技术在飞机液压系统中的应用[J].计算机辅助工程,2006,5(2):42-45. GUO Jun，WU Yafeng，CHU Nisheng. Application of AMESim in Aircraft Hydraulic System[J].Computer Aided Engineering,2006,15(2):42-45.

[5] 胡均平,刘成沛,郭勇，等.液压打桩锤主控滑阀稳态液动力研究[J].合肥工业大学学报(自然科学版),2011,34(12)：1787-1791． HU Junping，LIU Chengpei，GUO Yong，et al. Study of Steady-state Flow Force of Main Control Spool Valve of Hydraulic Pile Driving Hammer[J].Journal of Hefei University of Technology(Natural Science),2011,34(12)：1787-1791．

[6] 周华刚,曹春泉,余慧玲.飞机液压助力器模型分析[J].机床与液压,2014,42(7):137-140. ZHOU Huagang，CAO Chunquan，YU Huiling. Analysis of Hydraulic Booster Model for Aircraft[J].Machine Tool & Hydraulics,2014,42(7):137-140.

[7] 陈宇金,李磊,万兴云.基于AMESim的直升机液压助力器建模与分析[J].直升机技术,2012(4)：45-51. CHEN Yujing，LI Lei，WAN Xingyun. Modeling and Simulation of Helicopter Hydraulic Actuater Based on AMESim[J].Helicopter Technique,2012(4)：45-51.

[8] 董振乐,马大为,姚建勇,等. 含磁滞补偿的电液伺服系统预设性能跟踪控制[J]. 中国机械工程,2016,27(8):995-1000. DONG Zhenle,MA Dawei，YAO Jianyong, et al. Prescribed Performance Tracking Control of Electro-hydraulic Servo Systems with Hysteresis Compensation[J].China Mechanical Engineering,2016,27(8):995-1000.

[9] 王玄，陶建峰,张峰榕,等. 泵控非对称液压缸系统高精度位置控制方法[J].浙江大学学报(工学版)，2016，50(4)：597-602. WANG Xuan,TAO Jianfeng, ZHANG Fengrong, et al. Precision Position Control of Pump-controlled Asymmetric Cylinder[J]. Journal of Zhejinag University(Engineering Science),2016，50(4)：597-602.

[10] 王建强,陈立群,夏永胜，等.非对称阀控非对称缸系统仿真与优化研究[J].合肥工业大学学报：自然科学版,2012,35(5)：595-597． WANG Jianqiang，CHEN Liqun，XIA Yongsheng，et al. System Simulation and Optimization Research on Asy-mmetric Cylinder Controlled by Asymm-etric Valve[J].Journal of Hefei University of Technology：Natural Science,2012,35(5)：595-597．

[11] 叶小华,岑豫皖,赵韩，等.基于液压弹簧刚度的阀控非对称缸建模仿真[J].中国机械工程,2011,22(1):23-27. YE Xiaohua，CEN Yuwan，ZHAO Han，et al. Modeling and Simulation of Hydraulic Spring Stiffness-based Asymmetrical Cylinder Controlled by Valve[J].China Mechanical Engineering,2011,22(1):23-27.

[12] 陈佳,邢继峰,彭利坤. 基于传递函数的数字液压缸建模与分析[J].中国机械工程,2014,25(1):65-70. CHEN Jia，XING Jifeng，PENG Likun. Modeling and Analysis of Digital Cylinder Based on Transfer Function[J]. China Mechanical Engineering,2014,25(1):65-70.

(编辑 袁兴玲)

作者简介：陈 剑，男，1962年生。合肥工业大学噪声振动工程研究所教授、博士研究生导师。主要研究方向为汽车NVH与CAE、机器低噪声设计、液压系统振动与噪声控制。发表论文50余篇。邓支强，男，1991年生。合肥工业大学噪声振动工程研究所硕士研究生。乔晋红，男，1989年生。合肥工业大学噪声振动工程研究所硕士研究生。

Aircraft Hydraulic Booster and Rudder System Modeling and Performance Simulation

CHEN Jian DENG Zhiqiang QIAO Jinhong

Institute of Sound and Vibration Research, Hefei University of Technology, Hefei,230009

A simulation model for analyzing a hydraulic booster and rudder system was established based on a typical hydraulic booster of a certain type of aircraft flight control system. The system model that consisted of the dynamics of load, piston, cylinder, and spool of the valve was derived by considering the influences of nonlinear factors such as oil stiffness, structure stiffness, friction and leakage. The influences of key parameters on the system performance and stability were analyzed and elaborated by focusing on the system stability and static dynamic characteristics. The simulation results show that this system has good stability and quick response, as well as good performance in both of static and dynamic.

hydraulic booster; flight control; stability; static and dynamic characteristics

文 静，女，1992年生。上海大学机电工程及自动化学院硕士研究生。主要研究方向为机械设计。E-mail：1562851783@qq.com。何永义，男，1965年生。上海大学机电工程与自动化学院研究员、博士研究生导师。

2016-05-27

V249.11

10.3969/j.issn.1004-132X.2017.07.008