机械解耦自标定并联六维力传感器设计及仿真
赵延治 焦雷浩 牛 智 鲁 超 赵铁石
1.燕山大学河北省并联机器人与机电系统实验室,秦皇岛,河北,0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学),秦皇岛,河北,066004
机械解耦自标定并联六维力传感器设计及仿真
赵延治1,2焦雷浩1,2牛 智1,2鲁 超1,2赵铁石1,2
1.燕山大学河北省并联机器人与机电系统实验室,秦皇岛,河北,0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学),秦皇岛,河北,066004
针对传统多维力传感器研制后均需繁冗的加载标定这一现状,提出了多维力传感器“自标定”设计理念,通过钢球滚动机械解耦,设计了一种弱耦合全压向力自标定正交并联六维力传感器结构。论证了该六维力传感器的滚动解耦原理,分析了其自标定原理。基于螺旋理论建立了该六维力传感器理想数学模型,计算得到其一阶静力影响系数矩阵。考虑分支弹性变形,基于高次超静定结构力学求解原理,对该六维力传感器进行了受力分析与仿真计算,结合数值算例论证了其自标定特性,从而为该新型六维力传感器的研制奠定基础。
六维力传感器;正交并联;机械解耦;自标定
0 引言
多维力传感器因其能够测量空间多维力信息,在机械加工、汽车制造、智能化机器人以及航空航天等领域有着重要的应用价值[1]。近年来,随着航空航天技术的发展,大量程多维力传感器被应用到风洞试验、火箭发射架测力、起落架校准以及航天器对接等试验中[2]。
多维力传感器的弹性体结构决定了其性能的优劣而成为研究的核心问题。考虑到并联机构具有结构紧凑、刚度高、力映射简明等优点,研究者将其应用于多维力传感器的结构设计。KANG[3]研制了基于Stewart并联结构的六维力传感器,并对其进行了结构优化设计;RANGANATH等[4]提出了基于Stewart平台的六维力传感器新构型;GAO等[5-6]采用弹性铰链来替代球面副,研制了系列小型化六维力传感器,并将其应用于机器人多指灵巧手抓取。在大量程多维力传感器研究方面,王洪光等[7]研制了一种大量程Stewart结构六维力/力矩传感器,并采用分支轮换法辨识了传感器的结构参数;贾振元等[8-9]设计并研制了一种利用压电石英作为力敏元件的新型并联式压电六维力传感器,并进行了静态和动态标定试验研究;LI等[10]基于传统并联结构设计了一种压电式重载六维力传感器;王志军等[11]研制了一种双层预紧式六维力传感器,并进行了静态解耦试验研究;ZHAO等[12]研制了大量程柔性铰并联六维力传感器及其加载标定实验系统,提出了12分支过约束并联六维力传感器结构。由于采用传统铰接的多维力传感器存在铰链间隙及摩擦,维间耦合较大,因此普通多维力传感器研制后均需对其进行繁冗的整体加载标定。当前还没有适用于空间多维力加载的通用多维力标定装置,因此还需要研制专型专用的加载标定实验装置,特别是对于大量程重载多维力传感器的加载标定,即便研制出通用高精度空间多维力加载装置,实现多维力传感器的加载标定也存在着工作量大、周期长、费用高等问题,因此,多维测力传感器的加载标定已成为制约重载多维测力传感器研制的技术瓶颈。
本文提出了多维力传感器“自标定”的设计理念,设计了一种全压向力弱耦合自标定并联六维力传感器新结构,即通过采用钢球滚动解耦,辅以并联正交分布测力分支,构建多分支过约束传感器结构。基于螺旋理论建立了该六维力传感器的数学模型,采用高次超静定结构力学求解原理进行受力分析与仿真计算,论证了该六维力传感器的解耦性以及自标定特性。
1 机械解耦自标定并联16分支六维力传感器设计
1.1 多维力传感器自标定原理
为简化当前多维力传感器研制过程中后续繁冗的加载标定工作,本文提出了多维力传感器“自标定”设计理念。多维力传感器自标定就是多维力传感器研制后无需对其进行空间多维力整体加载标定,仅通过简明的结构几何关系及其内部单维力传感器测力信息就可得到被测量外力的全部信息。通过对解耦测力单元结构及其所用材料进行特殊设计,最大限度地将其传感器加载外力解耦映射为各测力分支单维力,从而满足加载载荷对力传感器的单向传递,实现多维力传感器的维间解耦测量,进而使得对多维力传感器的标定可通过对内部单维力传感器的标定来实现,即实现了多维测力传感器的自标定。可见,满足多维力传感器“自标定”设计理念须满足以下条件:测力分支内部分布单维力传感器;传感器弹性体结构具有简明的结构几何关系;测力分支之间相互干扰要小,即满足力解耦单向传递。
1.2 传感器结构设计
图1所示为机械解耦全压向力自标定并联16分支六维力传感器结构。该传感器由加载板、连接板、盖板、固定基座、16条解耦测力分支组成。固定基座为框架结构,与盖板通过螺栓连接后形成一个箱体,加载板与连接板通过4根螺柱连接,连接板与盖板以及固定基座通过16条解耦测力分支相连接,16条测力分支分布于连接板的6个侧面,在连接板上面和下面各设有4条测力分支,4个侧面上各设有2条测力分支,处在同一面上的测力分支的中心线相互平行,相邻面上的测力分支中心线相互垂直。每条解耦测力分支分别由单维力传感器、上连接弧面、下连接弧面、钢球组成,单维力传感器一端固定在固定基座或上盖板上,另一端与下连接弧面的平面端固定,上连接弧面的平面端固定在连接板上,其弧面端与下连接弧面的弧面端将钢球镶嵌在中间,该全压向力正交16分支并联六维力传感器结构整体呈完全对称形式。
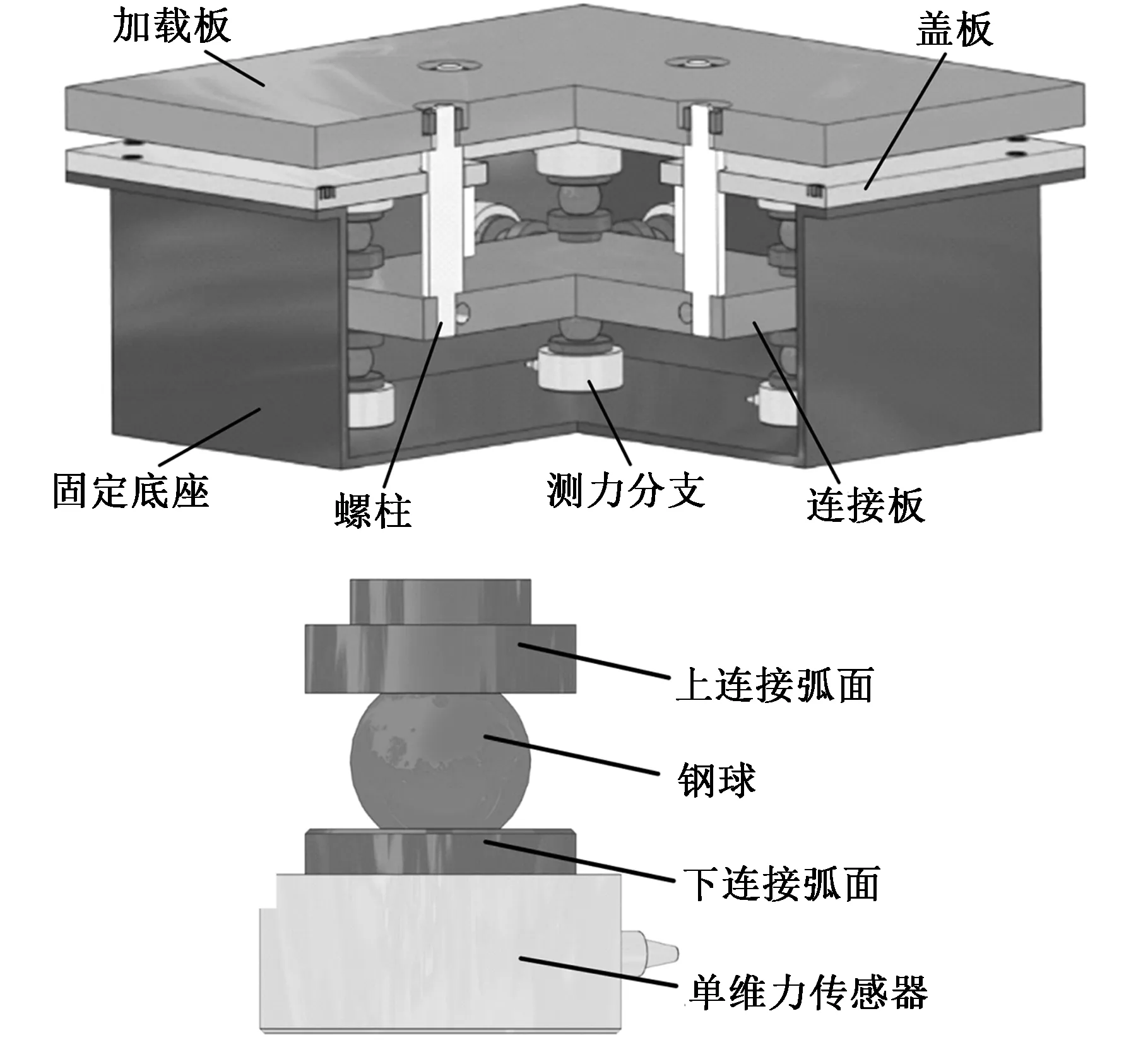
图1 正交并联16分支六维力传感器Fig.1 The orthogonal parallel 16 branches of six dimensional force sensor
1.3 六维力传感器自标定原理
根据多维力传感器“自标定”设计原理,在满足测力分支耦合小的基础上,传感器弹性体结构还应具有简明的结构几何关系。因此,在上述机械解耦基础上,引入冗余测力分支以及并联正交分布形式的设计,构建了该正交16分支并联六维力传感器过约束结构,该结构可大幅度提高传感器结构刚度和承载能力,进而提高力传递能力,满足大型六维力传感器承受重载的要求,同时降低了并联多维力传感器维间耦合,实现多分量力解耦测量,进而只需标定单维力传感器即可实现对多分量测力系统的整体标定。
如图2所示,传感器16条分支采用正交式布置形式,8条垂向解耦测力分支对称布置于连接板上下平面,可实现单维z轴向力的测量,同时又可完成x、y轴二维力矩测量。8条水平解耦测力分支布置于连接板四侧面,可实现x、y轴二维轴向力的测量,同时可完成z轴力矩测量。外载荷与解耦测力分支的对应关系见表1。
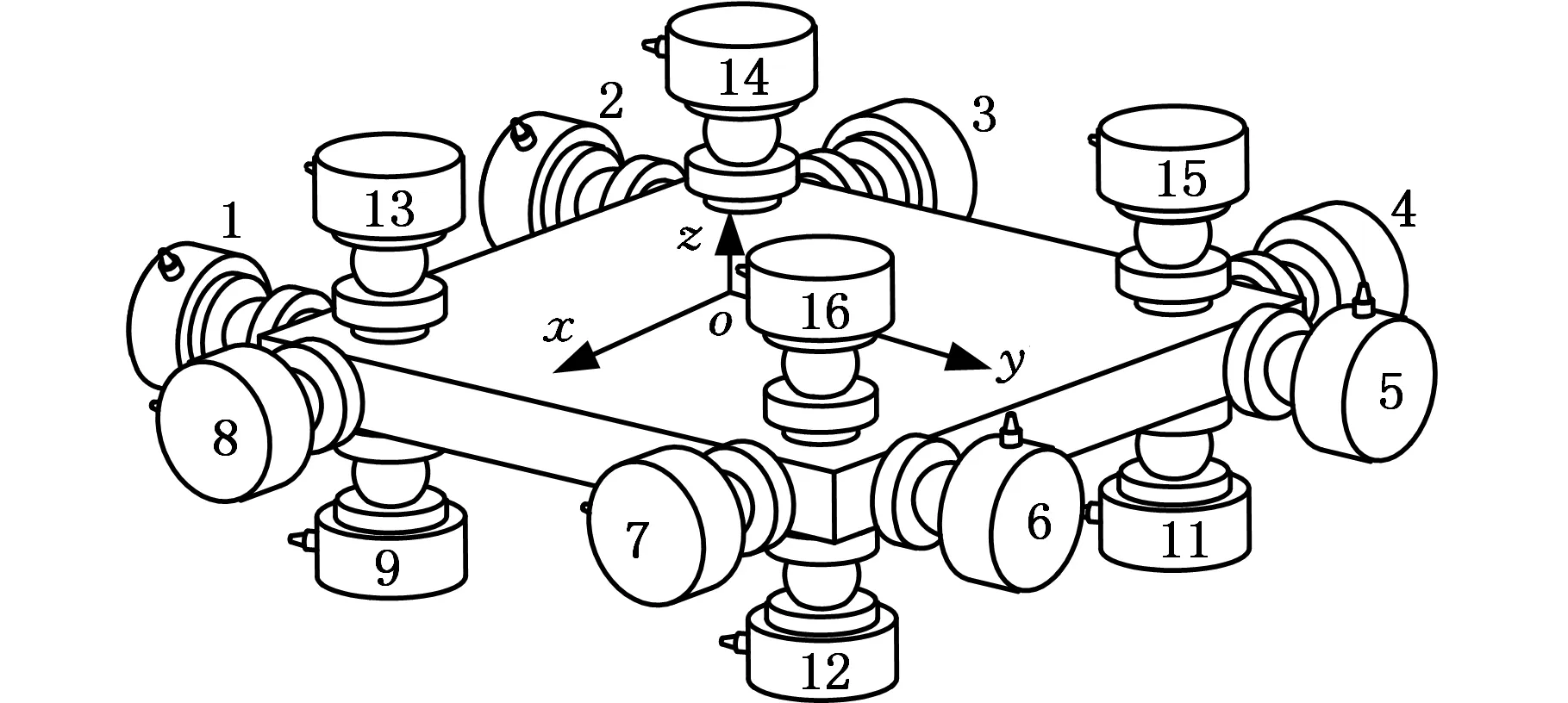
图2 传感器分支布局图Fig 2 The scheme of sensor branch layout

表1 六维力传感器测力原理表
2 传感器理想测量模型建立
图3为该六维力传感器结构参数示意图,坐标系oxyz为固定于连接板几何中心处坐标系,其三坐标轴方向分别为各测量分支轴线方向,将连接板与测力分支连接点记为ai(i=1,2,…,16),同时将测力分支与固定基座连接点记为bi(i=1,2,…,16),各测力分支两端点分别对应的位置矢量记为Ai(i=1,2,…,16)和Bi(i=1,2,…,16)。连接板宽为a,长为b,坐标系x轴方向上的测量分支间距离为c;坐标系y轴方向上的测量分支间距离为d。图5中,F=(Fx,Fy,Fz)T和T=(Tx,Ty,Tz)T分别表示连接板受到的外力以及外力矩。

图3 16分支六维力传感器结构示意图Fig.3 The structure diagram of the 16 branches of six dimensional force sensor
对于该并联16分支六维力传感器,若忽略各分支及结构的微小弹性变形,则基于螺旋理论[13],得到该传感器结构的静力平衡方程为
(1)
其中,FW=(F,T)T为施加于连接板上的广义外力;fi(i=1,2,…,16)为第i个测力分支的内力;$i=(Si,S0i)T(i=1,2,…,16)表示第i个测力分支的单位方向矢量,同时存在关系式Si=(Ai-Bi)/|Ai-Bi|,S0i=(Bi×Ai)/|Ai-Bi| 。则式(1)可分解表示为
(2)
(3)
其矩阵形式为
(4)
因此,该六维力传感器的静力平衡方程为
FW=Gf
(5)
G=[S1S2…S16S01S02…S016]
f=[f1f2…f16]T
式中,G为该六维力传感器的静力影响系数矩阵。
结合图3所示该新型并联16分支传感器结构参数,可得该传感器理想情况下的静力影响系数矩阵为
(6)
3 传感器典型工况下受力分析与仿真
该新型机械解耦全压向力式正交16分支并联六维力传感器结构属于高次超静定结构,由于各分支并非刚体结构,所以在建模过程中应考虑各测力分支轴向的变形。基于高次超静定力学求解原理[14]分别对传感器各维加载情况进行了分析与仿真计算。由于篇幅所限,在此仅对水平力以及力矩加载两种情况进行计算分析。
3.1 传感器水平加载
如图4所示,当该新型六维力传感器在水平方向加载Fy时,传感器连接板沿加载力方向移动距离为Δ1。由于该超静定结构六维力传感器采用预紧式连接,且各分支呈对称分布,所以各垂向测力分支会产生相应的抵抗力,而连接板在垂向产生位移Δ2。

图4 传感器水平力加载示意图Fig.4 The horizontal force loading diagram of the sensor
根据图5a所示的垂向测力分支9,10,…,16变形前后所处空间位置的几何关系,可以得到变形协调方程为
(7)
式中, fai为分支9,10,…,16 所受轴向力,fai=fa(i=9,10,…,16);l为测力分支等效长度;E为测力分支等效弹性模量;A为垂向测力分支等效横截面积。
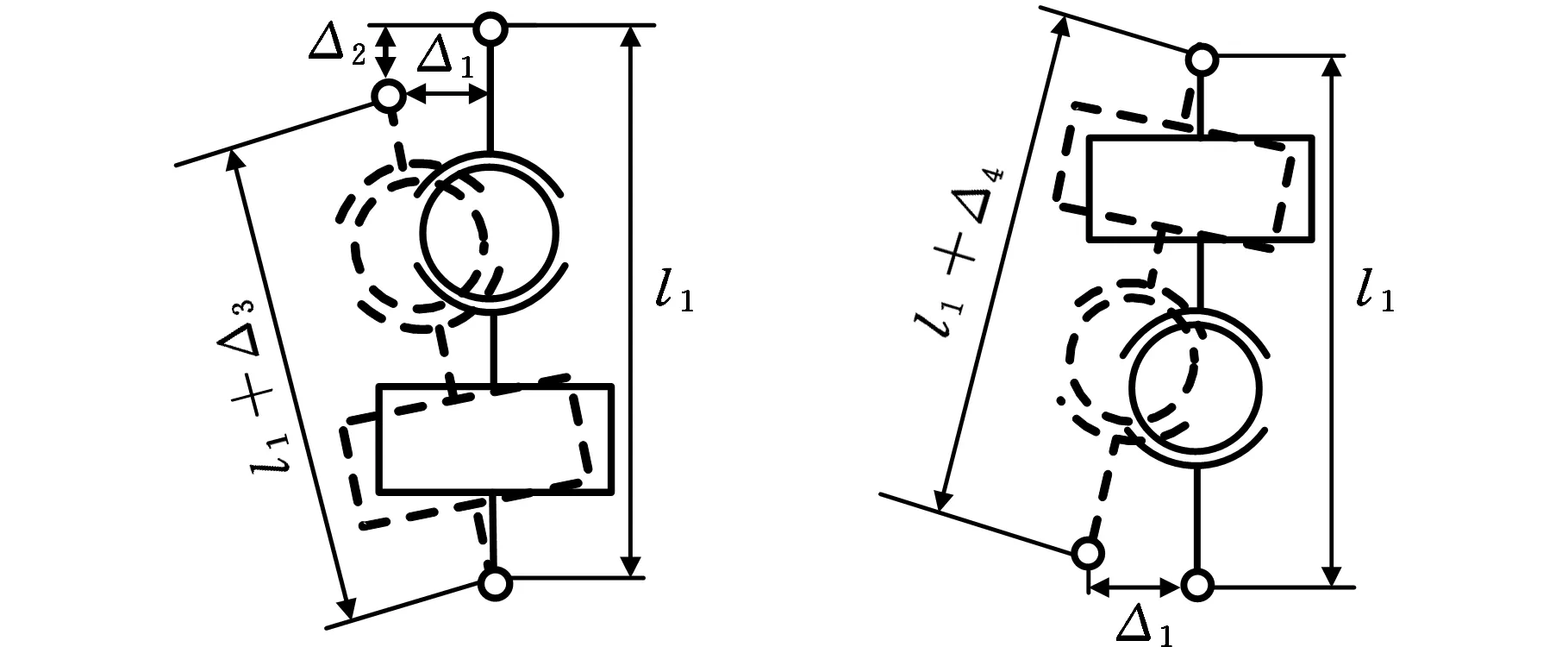
(a)分支9,10,…,16变形图(b)分支3,4,7,8变形图图5 与力方向垂直分支变形示意图Fig.5 The deformation diagram of the branches perpendicular to the direction of the force
与施力方向垂直的水平测力分支3,4,7,8将会产生整体分支的转动,且各水平测力分支轴向力相等,则根据图5b所示的与施力方向垂直的水平测力分支变形前后所处空间位置的几何关系,可以得到变形协调方程为
(8)
式中, fai=fb(i=3,4,7,8)为分支3,4,7,8 所受轴向力大小。
与施力方向平行的水平测力分支将会产生轴向上的变形以及整体分支的转动,且各测力分支轴向力相等。根据图6所示的与施力方向平行的水平测力分支变形前后所处空间位置的几何关系,可以得到变形协调方程为
(9)
式中,fai=fc(i=1,2)为分支1,2 所受轴向力大小。
(10)
式中, fai=fd(i=5,6)为分支5,6 所受轴向力大小。
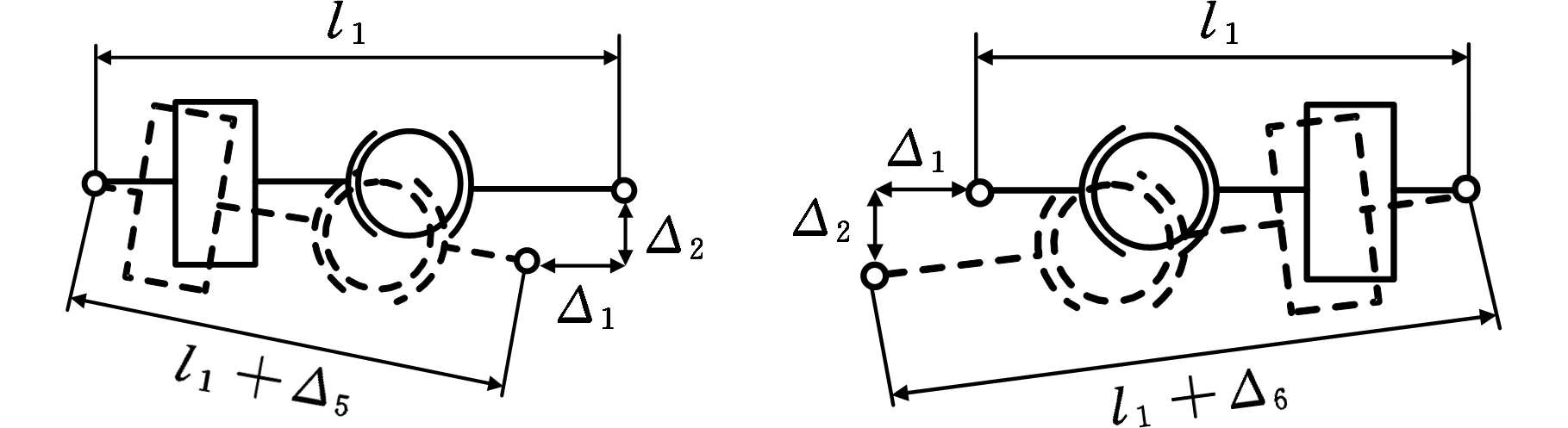
(a)分支1,2变形图(b)分支5,6变形图图6 与力方向平行分支变形示意图Fig.6 The deformation diagram of the branches parallel to the direction of the force
(11)
综上得水平加载情况下,传感器受力方程为
(12)
3.2 传感器力矩加载
图7为传感器受绕z轴的力矩加载的示意图。假设固定基座、连接板以及各铰链连接处均为刚性,同时不计各运动副摩擦。根据对称性可知,测力板上下面的4条垂向测力分支均发生相同的变形,因此其中的剪切力也必然相同,且8条水平测力分支中相对的分支也会产生相同的切向变形。图7中,fta、ftb、ftc为对应测力分支所受切向力, fa5、fa6为对应测力分支所受轴向力。

图7 传感器力矩加载示意图Fig.7 The torque loading diagram of the sensor
在扭矩载荷作用下各垂向测力分支球铰会产生相同切向位移变化,由于测力板为刚性,轴向位移Δ微小,因而忽略不计。根据单位载荷法并结合图8a,可以得到关系式:
Δ=Δ9=ftkl/(GA)
(13)
其中,ftk=fta(k=9,10,…,16),Δ9为垂向测力分支切向变形量,G为测力分支等效切变模量。
根据图8b和图8c所示的对应水平测力分支变形前后所处空间位置的几何关系,可以得到变形协调方程为
Δ10=ftkl/(GA)
(14)
ftk=ftb(k=3,4,7,8)
(l+Δ12)2+[ftkl/(GA)]2={l+[fa5l/(EA)]}2
(15)
ftk=ftc(k=1,2,5,6) fa5=fa6
式中,Δ10、Δ12为对应测力分支切向变形量。
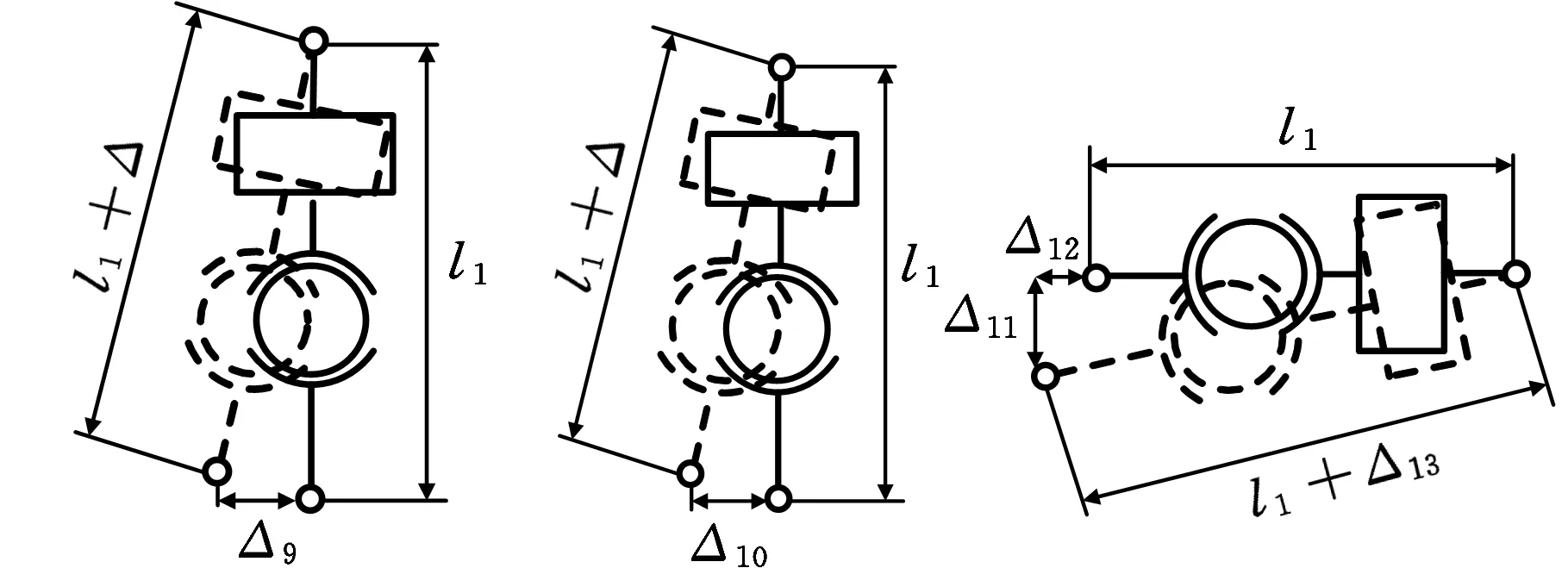
(a)分支9,10,…,16变形图(b) 分支3,4,7,8变形图(c)分支1,2,5,6变形图图8 传感器分支力矩加载变形示意图Fig.8 The sensor branches deformation schematicdiagram when loaded with torque
根据连接板的力矩平衡方程∑T=0得
∑T=ftac+ftba+ftcb-Fzc=0
(16)
综上得传感器受绕z轴的力矩加载情况下,传感器受力方程为
(17)
4 六维力传感器数值算例与分析
4.1 单维加载数值算例分析
根据上述分析,假设图3所示机械解耦并联16分支过约束六维力传感器中结构参数如下:各水平测量分支轴向刚度为1.884×109m/N,各垂向水平测量分支轴向刚度为4.884×109m/N。其他参数取a=2m,b=2m,c=1.7m,d=1.7m。根据对应的力映射模型得到分别对测力板施加的单维方向力、力矩以及复合力。结合传感器静力平衡方程式(5)、式(6)以及给定的正交16分支的具体参数,得到该全压向力16分支六维力传感器的输入输出力映射关系为
(18)
式中,f′为测力分支的内力与预紧力的合力,即分支传感器的输出示数。
为验证该传感器的解耦性,依据传感器输入输出力映射关系,在此列出单维x轴向力(Fx,0,0,0,0,0)T加载时各传感器的输出示数,见图9a,并给出与加载方向垂直的分支输出力映射曲线放大图,见图9b。力最大加载至20 kN,力矩最大加载至20 kN·m。

(a)单维x轴向力加载时各分支力曲线
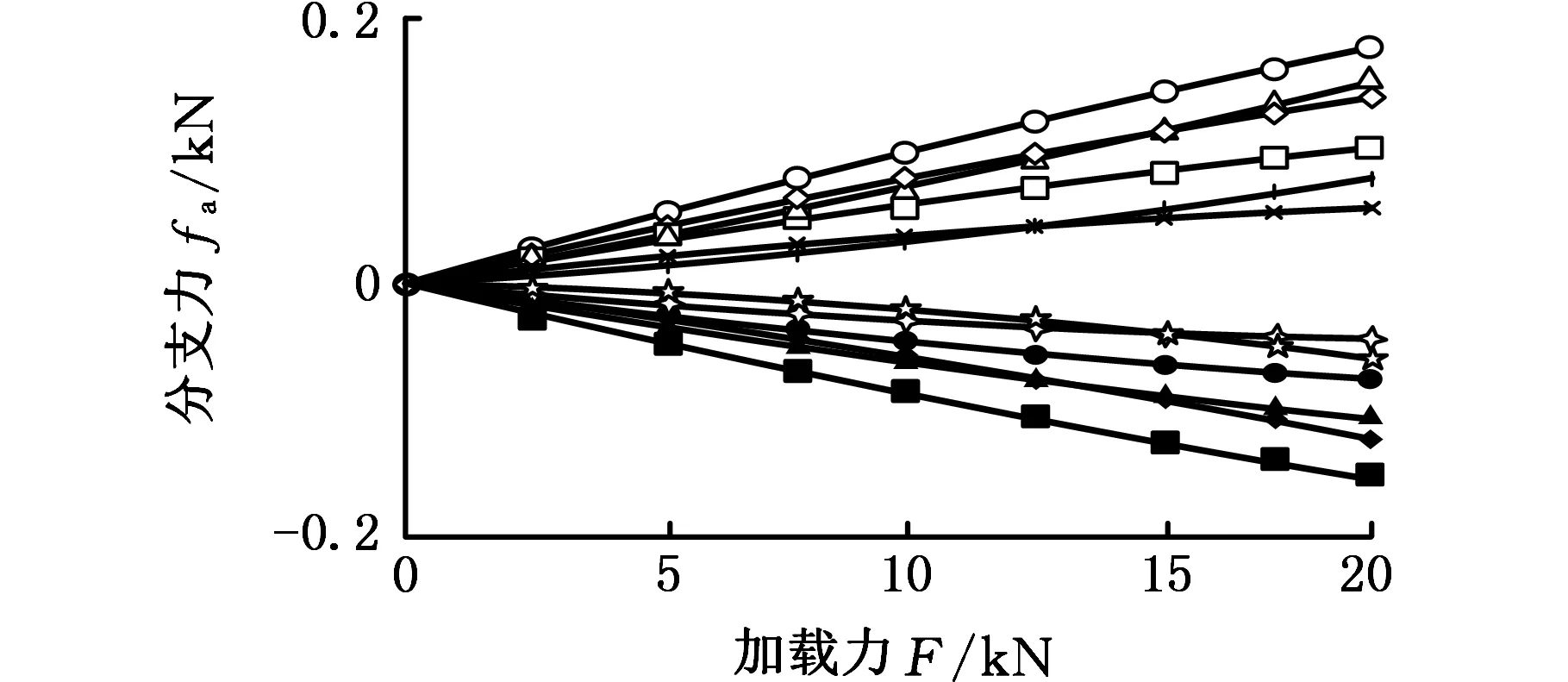
(b)单维x轴向力加载时分支力放大曲线图

图9 单维力加载时分支力曲线
由各传感器受力曲线可以看出,单维力加载时,与加载方向平行的分支输出示数随着外载荷的增大而增大,而与加载方向垂直的其他分支输出示数较小,从而证明单维力加载时,载荷主要传递到与其平行的单维力传感器,且分支间的耦合影响较小。
4.2 复合加载数值算例分析
单维加载时,采用单维外载荷逐步增大的方式绘制输入输出曲线,复合加载时,采用复合力同时均匀加载至最大值的方式绘制输入输出曲线。依据传感器输入输出力映射关系式,在此列出x轴与y轴轴向力(Fx,Fy,0,0,0,0)T复合加载时各传感器的输出示数(图10a),并给出与加载方向垂直的分支输出力映射曲线放大图(图10b),力最大加载至20 kN,力矩最大加载至20 kN·m。

(a)x轴、y轴轴向力复合加载时分支力曲线
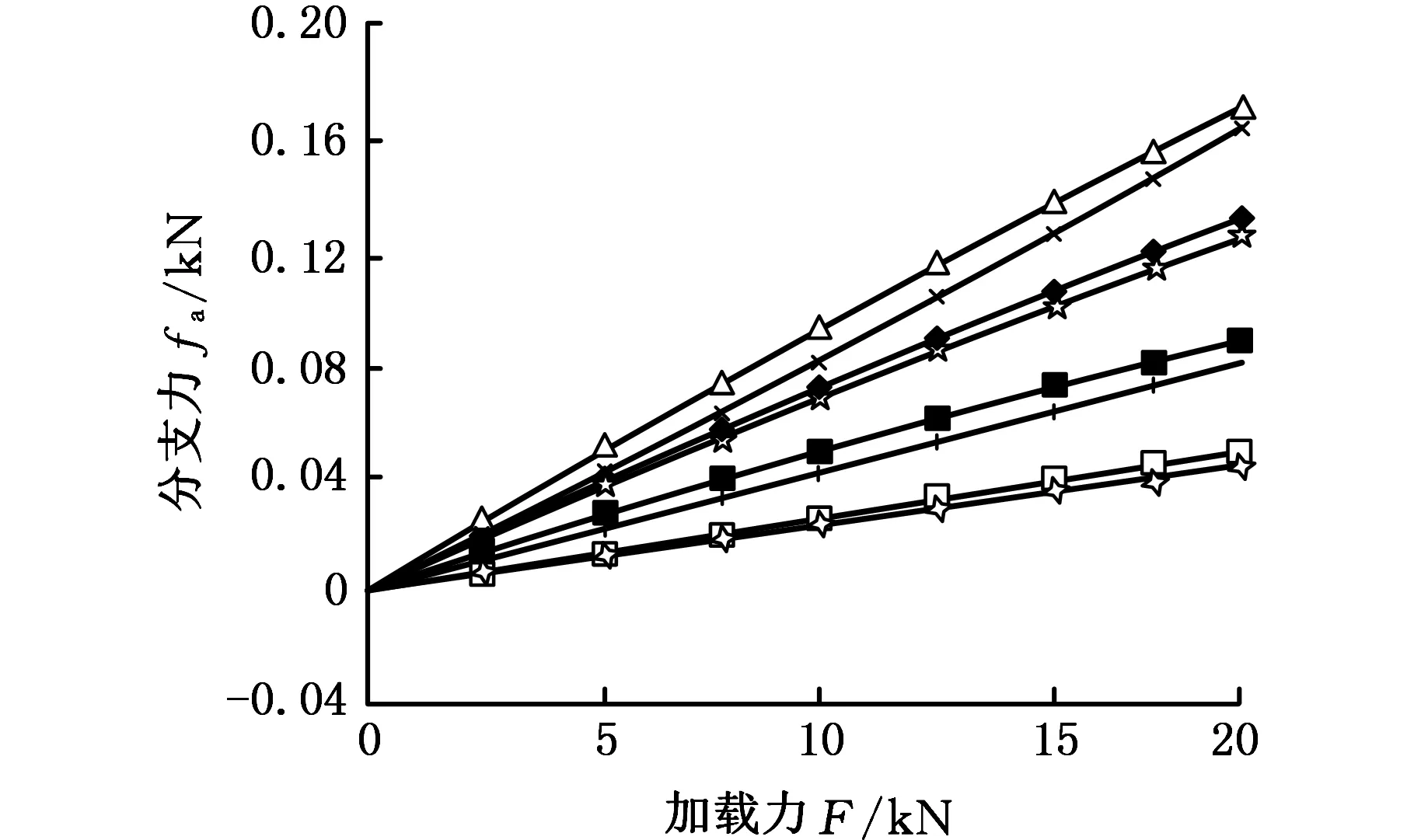
(b)x轴、y轴轴向力复合加载时分支力曲线放大图

图10 复合力加载时分支力曲线
由图10可以看出,复合力加载时,与加载力方向垂直的传感器各分支示数较小,同样也说明分支间的耦合影响较小。综上可看出,该正交并联传感器受到外载荷作用时,钢球解耦效果良好,分支间耦合影响较小,从而为自标定型传感器设计奠定了基础。
5 六维力传感器自标定原理验证
5.1 自标定原理数值算例验证
依据表1所示该机械解耦全压向力自标定并联六维力传感器的测力原理,对各分支施加足够大预紧力,当单维x轴向力(Fx,0,0,0,0,0)T加载时,x轴向传感器示数如图11所示。
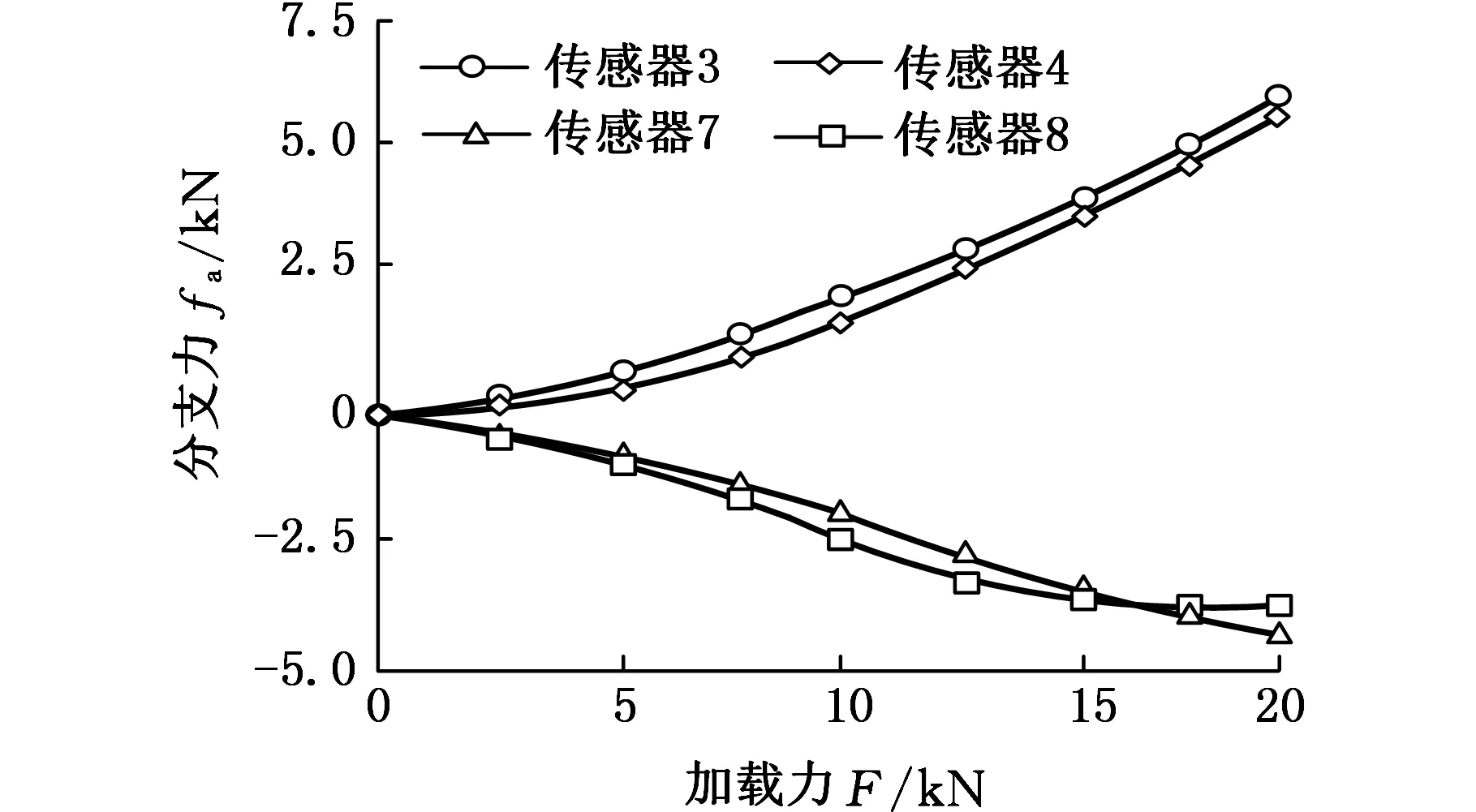
图11 单维x轴向力加载时分支力曲线Fig.11 Each branch force of x-axial when loading along x-axial
对于不同的加载点,各对应分支传感器输出示数以及对应误差如表2所示。

表2 单维x轴力加载误差分析表
当单维x轴向力矩(0,0,0,Tx,0,0)T加载时,z轴正负向传感器输出示数如图12所示。
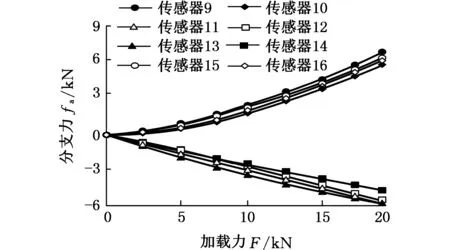
图12 单维x轴力矩加载时分支力曲线Fig.12 Each branch force curve when loading with single dimensional torque along x-axial
联立传感器设计参数,当单维x轴力矩加载时,对于不同的加载点,各对应分支传感器输出示数以及对应误差如表3所示。
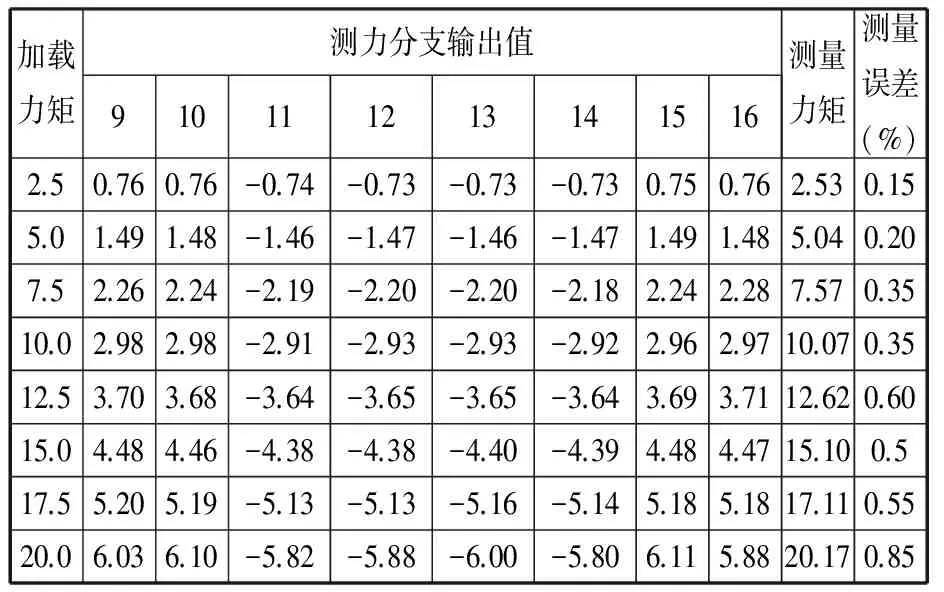
表3 单维x轴力矩加载误差分析表
由上述误差数据分析知,该机械解耦全压向力自标定并联16分支六维力传感器受到外载荷作用时,满足加载载荷对力传感器的单向传递要求,对测力系统的标定可通过对内部力传感器的简单标定来实现,使得各分支测力值有效叠加为实际受力,即实现了多维测力传感器的自标定设计。
5.2 自标定原理仿真验证
为进一步验证该机械解耦全压向力自标定并联16分支六维力传感器结构的自标定性能,利用仿真软件RecurDyn进行模拟仿真。将上述模型导入RecurDyn中,采用RecurDyn自带的mesh工具对构件进行柔性化处理,柔性体模型如图13所示,对该传感器加载大小为20 kN的x轴向力,加载模型如图14所示。

图13 传感器柔性体模型图Fig.13 The flexible body model of the sensor

图14 单维x轴向力加载仿真模型Fig.14 The simulation model when loading along x-axial
由于仿真初始阶段各构件发生变形,钢球发生微转动,会出现微小波动,故取仿真的稳定数据作为仿真有效值。取各加载点的传感器3数据与计算结果进行对比。理论计算结果与仿真结果对比如图15所示。
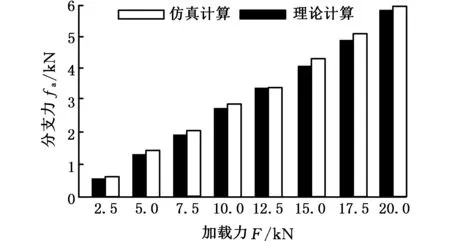
图15 单分支示数理论计算与仿真结果对比Fig.15 The single branch number comparison between theoretical calculation and simulation
对传感器施加外载荷,每次增加2.5 kN,最大增加到20 kN,则其理论计算与仿真结果如图16所示。

图16 传感器综合理论计算与仿真结果对比Fig.16 The comprehensive comparison between theoretical calculation and simulation
由上述仿真结果以及与理论计算的对比可看出,该机械解耦全压向力自标定并联16分支六维力传感器理论计算值与仿真结果误差较小,误差小于0.1%,从而进一步验证了理论计算的正确性,同时也证明了该传感器满足加载载荷对力的单向传递要求,实现了多维测力传感器的自标定。
6 结论
(1)提出了多维力传感器“自标定”设计理念,采用钢球滚动解耦,设计了一种弱耦合全压向力自标定正交并联16分支六维力传感器结构。
(2)建立了该六维力传感器数学模型,基于螺旋理论推导了传感器力映射关系。基于高次超静定结构力学求解原理,考虑分支弹性变形,对该传感器进行了典型工况下的受力分析与仿真计算。
(3)结合数值与仿真算例论证了该六维力传感器的解耦特性及其自标定特性,为该机械解耦自标定六维力传感器的研制奠定了基础,同时也对其他重载多维力传感器的研发提供了参考。
[1] 钟晓玲,张晓霞. 面向机器人的多维力/力矩传感器综述[J]. 传感器与微系统,2015,34(5):1-4.ZHONGXiaoling,ZHANGXiaoxia.ReviewofMulti-dimensionsForce/TorqueSensorforRobots[J].TransducerandMicrosystemTechnologies, 2015, 34(5):1-4.
[2] 戈瑜,吴仲城,葛运建.面向应用需求的力/力矩传感器技术发展动向[J].机器人,2003,25(2):188-192.GEYu,WUZhongcheng,GEYunjian.StateofArtsandDevelopmentTrendstowardApplicationOrientedForce/TorqueSensors[J].Robot, 2003, 25(2):188-192.
[3]KANGChulgoo.Closed-formForceSensingofa6-sixForceTransducerBasedontheStewartPlatform[J].SensorsandActuatorsA:Physical, 2001, 90:31-37.
[4]RANGANATHR,NAIRPS,MRUTHYUNJAYATS,etal.Aforce-torqueSensorBasedonaStewartPlatforminaNear-singularConfiguration[J].MechanismandMachineTheory, 2004, 39(9): 971-998.
[5]GAOF,ZHANGY,ZHAOXC,etal.TheDesignandApplicationsofF/TSensorBasedonStewartPlatform[C]//Proceedingsofthe12thIFToMMWorldCongress.Besancon,France, 2007: 11-16.
[6]GAOFeng,JINZhenlin.DevelopmentofaNewTypeof6-DOFParallelMicro-manipulatorandItsControlSystem[C]//Proc.IEEEInt.Conf.Robot.Intell.Syst.SignalProcess.Changsha, 2003:715-720.
[7] 王洪光,赵明扬,房立金,等. 一种Stewart结构六维力/力矩传感器参数辨识研究[J]. 机器人,2008,30(6):548-553.WANGHongguang,ZHAOMingyang,FANGLijin,etal.OnParameterIdentificationofaStewartPlatformBasedSix-componentForce/TorqueSensor[J].Robot, 2008, 30(6):548-553.
[8] 贾振元,李映君,张军,等. 并联式轴用压电六维力/力矩传感器[J]. 机械工程学报,2010 46(11):62-68.JIAZhenyuan,LIYingjun,ZHANGJun,etal.AxialPiezoelectric6-componentForce/TorqueSensorBasedonParallelStructure[J].JournalofMechanicalEngineering, 2010, 46(11): 62-68.
[9]JIAZhenyuan,LINSheng,LIUWei.MeasurementMethodofSix-axisLoadSharingBasedontheStewartPlatform[J].Measurement, 2010, 43:329-335.
[10]LIYingjun,SUNBaoyuan,ZHANGJun,et.al.ANovelParallelPiezoelectricSix-axisHeavyForce/TorqueSensor[J].Measurement, 2009,42:730-736.
[11] 王志军,姚建涛,吴遥,等. 双层预紧式六维力传感器及其静态标定[J]. 机械工程学报, 2013, 49(3):24-30.WANGZhijun,YAOJiantao,WUYao,et.al.DualLayersPre-stressedSix-axisForceSensorandItsStaticCalibration[J].Journalofmechanicalengineering, 2013, 49(3):24-30.
[12]ZHAOYanzhi,LUChao,ZHAOTieshi.SimulateCalculationofaNovelOver-constrainedParallelSixComponentForce/TorqueSensor[J].MachineDesignandResearch, 2013, 29(4): 22-29.
[13] 黄真,赵永生,赵铁石. 高等空间机构学[M]. 2版. 北京:高等教育出版社,2006: 296.HUANGZhen,ZHAOYongsheng,ZHAOTieshi.AdvancedSpatialMechanism[M]. 2ed.Beijing:HigherEducationPress, 2006: 296.
[14] 钱令希. 超静定与静定结构学[M]. 北京:科学出版社,2011:5-6.QIANLingxi.StaticallyIndeterminateandStaticallyDeterminateStructures[M].Beijing:SciencePress, 2011:5-6.
(编辑 苏卫国)
Design and Simulation of Mechanical Decoupling Self-calibration Parallel Six Dimensional Force Sensors
ZHAO Yanzhi1,2JIAO Leihao1,2NIU Zhi1,2LU Chao1,2ZHAO Tieshi1,2
1.Key Laboratory of Parallel Robot and Mechatronic System of Hebei Province,Yanshan University,Qinhuangdao,Hebei,066004 2.Key Laboratory of Advanced Forging & Stamping Technology and Science of Ministry of Education of China,Yanshan University,Qinhuangdao,Hebei,066004
To avoide the present situations of the heavy loading calibration of traditional multi-dimensional force sensors, a self-calibration design concept of multi-dimensional force sensors was proposed, the weak coupling full thrust force self-calibration orthogonal parallel six dimensional force sensor structure was design which might realize mechanical decoupling by the rolling of the steel balls. The rolling decoupling principles of the six dimensional force sensors were demonstrated, and then the self-calibration principles of the six dimensional force sensors were demonstrated. An ideal mathematical model of the six dimensional force sensors was established based on the screw theory, and the first order static influence coefficient matrix was obtained. The force analysis and simulation of the six dimensional force sensor were carried out with considering the elastic deformations based on the mechanics solution principles of high-order statically indeterminate structure, and the self-calibration characteristics were proved by combining the numerical examples, which sets the development foundation of the novel six dimensional force sensors.
six dimensional force sensor; orthogonal parallel; mechanical decoupling; self-calibration
2016-05-12
国家自然科学基金资助项目(51105322);河北省自然科学基金资助项目(E2014203176);河北省高等学校科学技术研究青年基金资助项目(QN2015040);中国博士后科学基金资助项目(2016M590212)
TH112
10.3969/j.issn.1004-132X.2017.07.003
赵延治,男,1981年生。燕山大学机械工程学院副教授。主要研究方向为并联机器人机构学理论与应用。发表论文30余篇。焦雷浩,男,1990年生。燕山大学机械工程学院硕士研究生。E-mail: 1522326790@qq.com。牛 智,男,1989年生。燕山大学机械工程学院博士研究生。鲁 超,男,1989年生。燕山大学机械工程学院硕士研究生。赵铁石,男,1963年生。燕山大学机械工程学院教授、博士研究生导师。

