基于压缩信息特征提取的滚动轴承故障诊断方法
孟 宗 李 晶 龙海峰 潘作舟
1.燕山大学河北省测试计量技术及仪器重点实验室,秦皇岛,0660042.北京精密机电控制设备研究所,北京,100076
基于压缩信息特征提取的滚动轴承故障诊断方法
孟 宗1李 晶1龙海峰2潘作舟1
1.燕山大学河北省测试计量技术及仪器重点实验室,秦皇岛,0660042.北京精密机电控制设备研究所,北京,100076
压缩感知作为一种新型压缩采样方法,利用信号稀疏特性以远低于奈奎斯特采样定理的采样速率压缩采集信号,减小数据采集、传输、存储的硬件压力。基于压缩感知框架下压缩采集的信号,提出了一种滚动轴承故障诊断新方法。该方法选择部分hadamard矩阵作为测量矩阵,将峭度因子、方差、波形因子作为敏感特征参量,不重构压缩测量量,直接利用压缩采集信息,提取敏感特征,然后通过PSO-SVM算法进行模式识别从而实现故障诊断。研究结果表明,在一定压缩比范围内,利用该方法能够在降低平均采样速率的同时用更少的数据量表现故障特征,实现滚动轴承故障诊断。
压缩感知;hadamard矩阵;特征提取;故障诊断
0 引言
故障诊断过程中,可靠的信息获取是故障诊断的前提,提取故障特征是故障诊断的必要条件[1]。
传统采样过程必须符合Shannon-Nyquist采样定理,即采样频率不低于采样信号最高频率的二倍。这样,采样频率仅由所采集信号频带决定,高频带信息采集受硬件限制、成本昂贵,且会产生海量数据造成数据冗余,数据的传输、存储、处理过程均受到采样过程限制。
压缩感知(compressed sensing,CS)理论是由DONOHO等[2-3]于2006年提出的一种新型信号采样方法。该理论利用信号自身或在某个变换基下的稀疏特性,应用一个与变换基不相关的观测矩阵观测信号,将高维信号投影到一个低维空间,再通过某种优化算法用这些少量投影高概率地重构出原信号,将硬件代价转化为软件代价,从而大大降低采样率[4]。这一过程包含三个重要问题:一是测量矩阵下信号压缩采集的硬件实现;二是测量矩阵和稀疏变换基的设计选取;三是重构算法的精度、效率。
目前压缩感知在图像处理、光谱分析等领域已得到广泛研究[5],针对机械故障振动信号的研究也逐步展开。在声学信号采集过程中,余恺等[6]提出一种基于压缩感知的声信号采集方法,该方法能够实现在1/10以下标准采样频率下的声信号采集。针对滚动轴承振动信号,张新鹏等[7]利用压缩感知理论实现轴承振动数据的修复;李鑫滨等[8]针对轴承故障信号特征特点对稀疏基进行改进以实现故障信号的快速高效稀疏分解,从而进行特征提取;郭俊峰等[9]通过选用更加合适的测量矩阵,在保证重构精度的情况下利用较高的压缩比压缩采集信号。在工程实际中,机械系统故障信号往往较复杂,信号稀疏特性差,信号重构难,并且故障信号重构将会花费大量时间,增加软件代价。
基于此,本文提出一种基于压缩感知的滚动轴承故障诊断方法,首先对测量矩阵和故障敏感特征参量进行分析,在压缩感知框架下利用测量矩阵以较低的平均采样率采集信号,直接对压缩采集信息进行敏感特征提取,无需重建信号也可进行较高效的故障诊断。
1 压缩感知
1.1 压缩感知数学模型
设长度为N的信号sN×1,该信号本身或在某个变换域下具有稀疏性。根据信号的稀疏程度及性质,设计观测矩阵ΦM×N(M≪N)和正交基字典矩阵Ψ,对稀疏信号进行线性变换,得到压缩感知数学模型:
Y=ΦΨs=Θs
(1)
其中,Y是在压缩感知理论框架下获取的M维采样信号;M称为矩阵的测度数;正交基字典矩阵Ψ称为变换基。
在满足式(1)的所有情况中,最稀疏解即为所求,即求解最优化问题:
(2)
式中,‖s‖0为s的l0范数。
求解极小化l0范数是一个N-hard的问题。引入限制等距约束(RIP)条件:
(3)
0<δk<1
式中,k为稀疏度;x为稀疏信号。
在观测矩阵满足RIP条件时,可将求解极小化l0范数问题转化为求解极小化l1范数问题:
(4)
通过求解式(4)可恢复出稀疏信号。根据RIP定理,观测矩阵和变换基的不相干程度越高,对信号稀疏程度的要求越低。
1.2 压缩信息采集原理
传统信号采样过程是信号从模拟到数字的转换过程,设采样时间间隔为T,该过程可表示为
y(nT)=
(5)
式中,x(t)为原始模拟信号;y(nT)为采集的数字信号;h(t)为滤波器。
传统信号采样过程原理见图1。其中,TNyq为奈奎斯特采样定理下的采样时间间隔。

图1 传统信号采样过程原理图Fig.1 Principle diagram of the traditional sampling process
传统采样过程必须遵循Shannon-Nyquist采样定理才能保证信号的无失真恢复。
采集到离散数字信号y(nT)后,一般可基于Whittaker-Shannon采样定理,根据下式将连续间隔数字信号重构成连续信号:
(6)
sinc(x)=sin(πx)/πx
根据压缩感知原理,如果信号在某一变换基下是稀疏的,通过一个与变换基不相关的观测矩阵,可以将信号从高维空间投影至低维空间,使得低维信号仍保留足够原信号信息,实现压缩采集。这种压缩信息采样过程是一种信号的模拟,即信息转换过程。完成这一过程的方法称为模拟/信息转换器(analog to information convertor,AIC)。目前已有多种AIC实现方案。以基于随机信号调制的AIC方案为例[10],该方案原理见图2。其中,Tcs为压缩感知框架下的采样时间间隔。

图2 压缩感知框架下AIC采样原理图Fig.2 Principle diagram of the AIC sampling process under the framework of compressed sensing
压缩感知框架下AIC采样表达式为
y(m)=(x(t)P(t))⊗h(t)|t=aTNyq
(7)
其中,P(t)是一个伪随机序列,它与测量矩阵有关。在一段时间间隔T内,应用传统采样方法采集N点信号,应用AIC采样方法采集M点信号,a=M/N(a<1),a是AIC采集所用时间与传统采集所用时间之比,以下简称压缩比。AIC采样方法的平均采样速率因此得到降低。
在实现时,这种采样方法相当于是分帧采样,每帧m个样本点,重构时分帧重构,每帧信号长度过短则不利于信息的完整性,每帧信号长度过长重构时间将会成倍增长,且不利于硬件的实现。
在压缩感知框架下,AIC采样设计实质上是在测量矩阵下采集信号的硬件实现方法。其中感知矩阵RIP特性对该方案性能起重要作用,因此测量矩阵的设计十分关键,一方面要考虑它与任意稀疏信号或稀疏基的不相关性,另一方面也要考虑硬件的实现和成本问题。
1.3 部分hadamard测量矩阵
定义1 一个N点离散时间信号x(n),且N=2q(q为正整数),其离散hadamard变化定义为
(8)
k=0,1,…,N-1
其中,bi(x)是非负整数二进制形式的第i位,如8的二进制形式可表示为1000,则b0(8)=0,b1(8)=0,b2(8)=0,b3(8)=1。离散hadamard变换用hadamard矩阵表示更为直观。
定义2 设一个矩阵是由+1和-1两种元素构成的正交方阵。即若满足:
HHT=nI
(9)
式中,I为一个单位矩阵。
则称H是一个n阶hadamard矩阵。二阶规范hadamard矩阵为
四阶规范hadamard矩阵为
已证明除了二阶规范hadamard矩阵外,hadamard矩阵的阶数均是4的倍数[11-12]。
离散hadamard变换可用hadamard矩阵表示:
XH(k)=x(n)H
(10)
根据压缩感知原理,可应用hadamard矩阵设计和构造常用且效果良好的测量矩阵——部分hadamard测量矩阵。信号在hadamard测量矩阵下采集,相当于对信号进行离散hadamard变换[13]。
构造部分hadamard测量矩阵,首先构造一个N×N的hadamard矩阵,然后抽取其中的M行,得到的M×N的矩阵即为测量矩阵,经该测量矩阵采集信号,长度为N的原始信息将映射到M维特征空间。该测量矩阵为确定性测量矩阵,构造方法简单,便于硬件和光学实现。
2 压缩感知框架下的滚动轴承故障诊断
在滚动轴承故障诊断过程中,振动数据采集的最终目的是能够提取故障信息。重构信号的过程是将采集信息转化成与原始模拟信号最相似的过程,重构信号的目的是能够更加顺利地进行特征提取,在故障诊断中信号重构实质是特征提取的一种手段[14]。数据的重构过程,伴随着重构误差和软件代价,故障信号的复杂性和非稀疏性对信号重构带来极大挑战。基于这种情况,本文提出一种在压缩感知框架下压缩信息采样的故障诊断新方法,根据测量矩阵与故障敏感特征信息参量性质,不重构信号,直接从少量观测值中提取故障特征信息,进行故障诊断。
本文选用部分hadamard测量矩阵。hadamard矩阵是正交矩阵,离散hadamard变换是正交变换,根据正交变换在欧氏空间中内积不变的性质,可以证明x(n)经离散hadamard变换后,序列能量保持不变,因此得到以下表达式:
(11)
由式(11)可知,数据经hadamard变换后能很好地保留原始数据的趋势特征,结合均方根公式,在hadamard矩阵下采集所得信号的均方根值与原始信号均方根值成正比。
当hadamard矩阵阶数较高时,hadamard矩阵中+1、-1个数接近。如768阶的hadamard矩阵中+1个数为295 296,-1个数为294 528。构造一个大小为768×64的部分hadamard观测矩阵,其中+1个数为249 60,-1个数为241 92,部分hadamard观测矩阵中+1和-1数量近似相等且比例各占1/2,可以看做是一个均值为0、方差为1的随机均匀分布的矩阵。在该测量矩阵下采样得到的数据对某些统计特征信息改变不大,对特定统计推理任务是有效的,可直接利用压缩采样信号提取故障特征信息。具体实现可分为三个部分:
(1)数据采集。应用压缩感知理论确定测量矩阵为部分hadamard观测矩阵,确定压缩比a,在测量矩阵下采集数据,得到轴承不同工作状态下各L帧数据、每帧M个样本点。
(2)特征提取。选择合适统计特征量作为故障特征参量,分别计算采样所得各组数据的特征参量。
(3)故障诊断。应用支持向量机算法理论进行故障诊断,先利用粒子群算法对SVM中参数进行寻优,得到最优参数后再对特征参量进行分类识别。
3 实验研究
3.1 实验对象
选择美国凯斯西储大学电气工程实验室的滚动轴承实验数据进行分析验证,待测滚动轴承型号为SKF6205,使用电火花加工技术分别在驱动端轴承外圈、内圈、滚动体上布置单点故障。故障尺寸为:深0.2794 mm,直径0.1778 mm。滚珠个数为9。轴承分别在正常、内圈故障、外圈故障、滚动体故障4种状态下工作,选择加速度传感器测量振动信号,以传统采样方法采集信号,采样频率12 kHz。得到数据如图3所示。

图3 滚动轴承故障信号Fig.3 Rolling bearing fault signal
3.2 可行性分析及特征提取
为证明本文方法可行,需要确定部分hadamard观测矩阵对特征参数的影响以及hadamard矩阵下特征参量的分布情况,从而挑选最合适的特征统计特征量作为特征参数进行特征提取。所选用的敏感特征参量如表1所示。
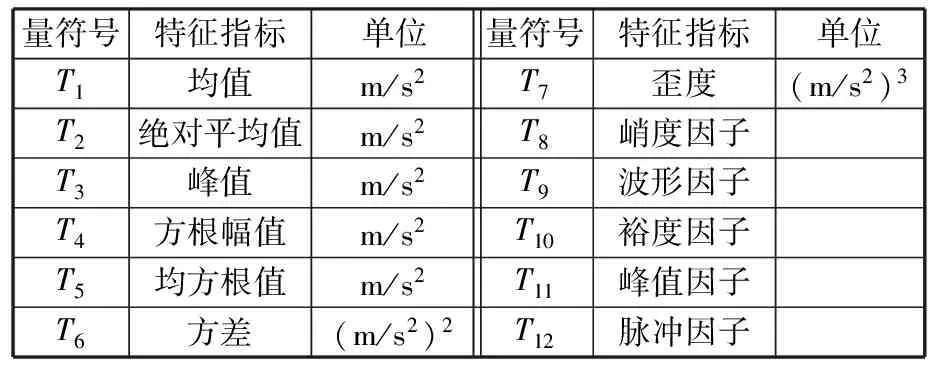
表1 敏感特征参量
测得轴承在正常情况、内圈故障、外圈故障、滚动体故障4种状态下驱动端振动数据,传统采样时,直接取25组数据,每组数据截取4096个样本点,计算每组数据的特征参量,轴承4种状态下特征参量的分布如图4所示。

图4 在传统采样方式下采集信号统计特征参数Fig.4 Sample signal statistical feature parameters under the traditional sampling method
在测量矩阵下采样时(非压缩情况),构造一个4096×4096的hadamard矩阵,在hadamard观测矩阵下逐帧采集轴承4种状态下的振动数据各25组,每组数据4096个样本点,计算特征参量值,得到特征参量分布,如图5所示。
对比图4、图5,采用hadamard观测矩阵采集数据,对T1、T7影响较大,影响各状态下的故障识别和分类;对T5数值上无影响;对T6、T2数值上影响很小;对T3、T4相对其他特征参量影响较大,但这些特征参量整体分布仍然遵循一定规律,对故障特征的分离和识别影响很小,与前文推理结果相一致;对T8至T12的影响较为复杂,其中对T8影响较小,不影响其特征分布,对T9的数值特征影响较小,但对其分布影响稍大。

图5 在hadamard矩阵下采集信号统计特征参数Fig.5 Sample signal statistical feature parameters under the hadamard matrix
在滚动轴承的状态监测和故障诊断中,有量纲参量相对分类效果较好但与设备状态有关,需综合应用有量纲和量纲一的敏感特征参量。其中方差能够直接反映振动能量的大小,波形因子对低频信号反映强烈,峭度因子对中高频信号较为敏感,是故障诊断中常用的特征参量[15-16]。综合图4、图5的分析说明,在hadamard矩阵下测量对信号的峭度因子、方差、波形因子影响有限,较其他特征参量性能更为理想,故选取峭度因子、方差、波形因子作为特征参量。
在本文采样方式下取轴承4种工作状态数据120组,每组768个采样点,计算各特征值,得到三维故障特征向量分布图,见图6。

图6 在hadamard矩阵下采集信号峭度因子、方差、波形因子分布Fig.6 Kurtosis factor, variance and waveform factor distribution of sampling signal under the hadamard matrix
由图6可以看出轴承4种状态下特征参量分布的不同,从而证明在hadamard矩阵下采集数据,用峭度因子、方差、波形因子作为特征参量提取特征从而进行故障诊断的方法是可行的。
3.3 基于压缩感知的故障诊断
就数据的压缩量对故障诊断效果影响作进一步研究。应用两种采样方法采集轴承在正常情况、内圈故障、外圈故障、滚动体故障4种状态下的数据。
对两种采样方法得到的故障识别率作比较。应用传统采样方式采集信号,每组信号长度为100点,应用本文采样方法在压缩比a=0.13的情况下采集信号,每组信号长度同样为100点,但信息长度相当于传统方法采集768点信息的长度。分别求4种状态下120组数据样本的敏感特征参量,得到图7、图8。
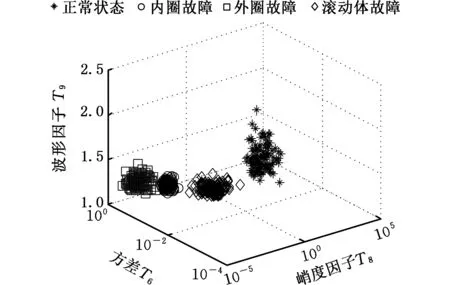
图7 本文方法特征参量分布情况Fig.7 Distribution of feature parameters under the method in this paper
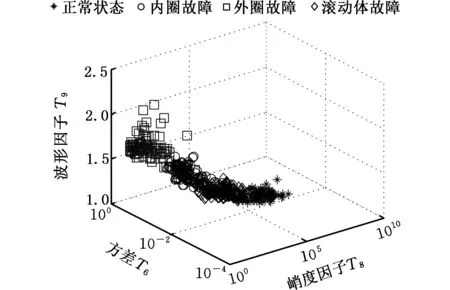
图8 传统方法特征参量分布情况Fig.8 Distribution of feature parameters under the traditional method
对比图7、图8可以清晰看出,应用本文方法采集数据,特征参量分布及各类样本更易区分。对数据进行分组,其中每种状态数据60组作为训练样本,60组作为测试样本,应用PSO-SVM算法分别计算其故障识别率,本文方法故障识别率为95.83%,传统方法故障识别率为89.58%,在采样点为100时本文方法故障识别率更高。
在数据压缩采集过程中,N值代表了每段信息的长度,M值代表了压缩采样下的测量点数,压缩比a=M/N。当N不变、M值减小时,每帧数据代表信息长度不变,测量点数减小,平均采样频率随M减小而减小;当M值不变、N值增大时,测量点数不变,每帧数据代表信息长度增大,平均采样频率随N增大而减小。
对比图6、图7,可以看出N不变情况下,测量值M的减小,对特征参量分布有一定程度的影响。进而作横向对比,N值设置为768,分别对两种采样方式得到不同长度数据进行特征提取和模式识别,数据长度范围为32~768点,每间隔4个数据点计算其故障识别率,得到结果如图9所示。根据图9可知,随着数据长度的减小,到一定程度后,统计特征量作为特征参数将不能完整地表现一个信号的特征,特征提取效果将会大大降低,故障识别率开始明显下降。测量点数在250~768之间时,本文方法与传统方法故障诊断率基本相同,在95%左右;当测量点数在60~250之间时,传统采样方式得到的信号长度不能满足特征提取的需要,故障识别率开始下降,应用本文方法采集的数据长度携带更多的信息量,其故障识别率高于传统采样方法,与之前的故障识别率基本相同。当数据长度降低至32~60点时,本文方法得到的故障识别率由于信息量不足也逐渐开始下降,传统方法得到的故障识别率仍然在继续下降。说明应用本文方法可以用更少的采样点实现故障诊断任务。

图9 两种方法故障识别率对比Fig.9 Comparison of fault recognition rate under two methods
为进一步验证本文方法优势,作纵向对比,测量点数M确定的情况下,不同信息长度N对故障识别率的影响如表2所示。
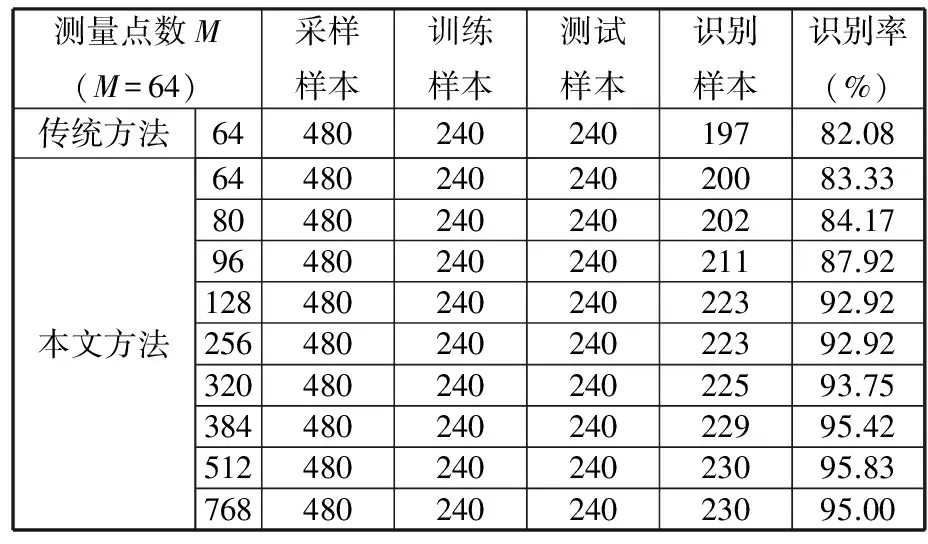
表2 不同采样信息长度下两种采样方式故障识别率分布对比
当采用传统采样方法采集数据,测量点数为64时,由于信号长度不够,表达特征不够准确,故障识别率仅82%左右;采用本文方法采集数据,当压缩比a=1,测量点数也为64时,故障识别率与采用普通采集方法得到的数据近似,对比图9中传统方法故障诊断率曲线,说明无论在哪种采样方式下,在信息长度不足时,故障信息无法被充足地提取出来。随着信息长度增长,在一定压缩比范围内,测量点数不变,随着N值逐渐增大,故障识别率逐渐提高,最终故障识别率提高到95%左右。M值不变的情况下,随着N值增大相同信息长度采样时间逐渐延长,一段时间内的平均采样率逐渐降低,说明应用本文方法实现故障诊断任务可有效降低平均采样率。
4 结论
(1)提出了一种基于压缩感知的故障诊断方法,根据在观测矩阵下压缩采集到的信号包含原来信号的大部分信息,平衡观测矩阵和故障特征参量的性能,直接将故障特征信息提取出来,而不需经过信号重构,实现信号压缩采集,且不影响故障信息提取。
(2)理论及实验证明,信号在部分hadamard测量矩阵下采集对某些反应故障特征的统计特征参量的影响程度有限,可直接进行特征提取,从而证明了本文方法可行。
(3)选用部分hadamard测量矩阵进行全局非自适应性测量采集信号,利用峭度因子、方差、波形因子作为特征参量提取故障信息,应用PSO-SVM算法进行故障诊断。滚动轴承故障诊断的实验表明,该方法较传统方法可以利用较少量采样点表达故障特征,降低了信号的平均采样率,实现故障诊断任务。
[1] 王国彪, 何正嘉, 陈雪峰,等. 机械故障诊断基础研究“何去何从”[J]. 机械工程学报,2013,49(1):63-72. WANG Guobiao, HE Zhengjia, CHEN Xuefeng, et al. Basic Research on Machinery Fault Diagnosis-What is the Prescription[J]. Journal of Mechanical Engineering,2013,49(1):63-72
[2] DONOHO D L. Compressed Sensing[J]. IEEE Transactions on Information Theory,2006,52(4):227-254.
[3] DONOHO D L, TSAIG Y. Extensions of Compressed Sensing[J]. Signal Processing,2006,86(3):533-548.
[4] 焦李成, 杨淑媛, 刘芳,等. 压缩感知回顾与展望[J]. 电子学报,2011,39(7):1651-1662. JIAO Licheng, YANG Shuyuan, LIU Fang, et al. Development and Prospect of Compressive Sensing[J]. Acta Electronica Sinica,2011,39(7):1651-1662.
[5] 宁方立, 何碧静, 韦娟. 基于lp范数的压缩感知图像重建算法研究[J]. 物理学报,2013,62(17):1-7. NING Lifang, HE Bijing, WEI Juan. An Algorithm for Image Reconstruction Based onlpNorm[J]. Chinese Journal of Physics,2013,62(17):1-7.
[6] 余恺, 李元实, 王智,等. 基于压缩感知的新型声信号采集方法[J]. 仪器仪表学报,2012,33(1):105-112. YU Kai, LI Yuanshi, WANG Zhi, et al.New Method for Acoustic Signal Collection Based on Compressed Sampling[J]. Chinese Journal of Scientific Instrument,2012,33(1):105-112.
[7] 张新鹏, 胡茑庆, 程哲,等. 基于压缩感知的振动数据修复方法[J]. 物理学报,2014,63(20):115-124. ZHANG Xinpeng, HU Niaoqing, CHENG Zhe, et al. Vibration Data Recovery Based on Compressed Sensing[J]. Chinese Journal of Physics,2014,63(20):115-124.
[8] 李鑫滨, 马阳, 邱建坤,等. 基于压缩感知弱匹配追踪算法的信号特征提取[J]. 中国机械工程,2014,25(24):3314-3319. LI Xinbin, MA Yang, QIU Jiankun, et al.Feature Extraction Based on Compressed Sensing Weak Matching Pursuit Algorithm [J]. China Mechanical Engineering,2014,25(24):3314- 3319.
[9] 郭俊峰, 施健旭, 雷春丽,等. 一种滚动轴承振动信号的数据压缩采集方法[J]. 振动与冲击,2015,34(23):8-13. GUO Junfeng, SHI Jianxu, LEI Chenli, et al. Data Compression Method for Collecting Rolling Bearing Vibration Signals[J]. Journal of Vibration and Shock,2015,34(23):8-13.
[10] 张弓, 文方青, 陶宇,等. 模拟-信息转换器研究进展[J]. 系统工程与电子技术,2015,37(2):229-238. ZHANG Gong, WEN Fangqing, TAO Yu, et al. Advances in Analog-to-information Convertor[J]. Systems Engineering and Electronics,2015,37(2):229-238.
[11] BANICAA T, SKALSKIB A. The Quantum Algebra of Partial Hadamard Matrices[J]. Linear Algebra and Its Applications,2015,34(11):364- 380.[12] 李明飞, 莫小范, 赵连洁,等. 基于Walsh-hadamard变换的单像素遥感成像[J]. 物理学报,2016,65(6):110-116. LI Mingfei, MO Xiaofan, ZHAO Lianjie, et al.Single-pixel Remote Imaging Based on Walsh-hadamard Transform[J]. Chinese Journal of Physics,2016,65(6):110-116.
[13] 韩娜, 滕少华, 房小兆. 基于hadamard变换的多元时间序列聚类研究[J]. 计算机工程与设计,2012,33(3):983-986. HAN Na, TENG Shaohua, FANG Xiaozhao. Mu-ltivariate Time Series Clustering Research Based on Hadamard Transform[J]. Computer Engineering and Design,2012,33(3):983-986.
[14] 刘冰, 付平, 孟升卫. 基于正交匹配追踪的压缩感知信号检测算法[J]. 仪器仪表学报,2010,31(9):1959-1964. LIU Bing, FU Ping, MENG Shengwei. Compressive Sensing Signal Detection Algorithm Based on Orthogonal Matching Pursuit[J]. Chinese Journal of Scientific Instrument,2010,31(9):1959-1964.
[15] 栗茂林, 梁霖, 王孙安. 基于稀疏表示的故障敏感特征提取方法[J]. 机械工程学报,2013,49(1):73-80. LI Maolin, LIANG Lin, WANG Sunan. Sensitive Feature Extraction of Machine Faults Based on Sparse Representation[J]. Journal of Mechanical Engineering,2013,49(1):73-80.
[16] 张绍辉, 李巍华. 基于特征空间降噪的局部保持投影算法及其在轴承故障分类中的应用[J]. 机械工程学报,2014,50(3):92-99. ZHANG Shaohui, LI Weihua. Locality Preserving Projections Based on Feature Space Denoising and Its Application in Bearing Fault Classification [J]. Journal of Mechanical Engineering,2014,50(3):92-99.
(编辑 袁兴玲)
Fault Diagnosis Method for Rolling Bearings Based on Compression Information Feature Extractions
MENG Zong1LI Jing1LONG Haifeng2PAN Zuozhou1
1.Key Laboratory of Measurement Technology and Instrumentation of Hebei Province,Yanshan University,Qinhuangdao,Hebei,066004 2.Beijing Research Institute of Precise Mechatronics and Controls, Beijing, 100076
As a new sampling method, compressed sensing samples with the signal sparse features were presented, which was far below the Nyquist sampling theorem. It might reduce generous requirements of data acquisition, transmission and storage hardware. Aiming at the signals from the compression perception within the framework, this paper proposed a new method for rolling bearing fault diagnoses. In this method, part of hadamard matrix was chosen as a measurement matrix, and kurtosis factor, variance and waveform factor as a sensitive parameters. So there was no need to rebuild compression measurement and the gathering informations were utilized to extract sensitive characteristics directly, and then the PSO-SVM algorithm was used for pattern recognition so as to realize fault diagnoses. It is shown that within a certain range compression ratio, the method may use less amount of data of fault characteristics for rolling bearing fault diagnoses.
compressed sensing; hadamard matrix; feature extraction; fault diagnosis
2016-05-20
国家自然科学基金资助项目(51575472);河北省自然科学基金资助项目(E2015203356);河北省高等学校科学研究计划资助重点项目(ZD2015049);河北省留学人员科技活动择优资助项目(C2015005020)
TN911;TH17
10.3969/j.issn.1004-132X.2017.07.009
孟 宗,男,1977年生。燕山大学电气工程学院教授、博士研究生导师。主要研究方向为振动信号分析与处理、旋转机械状态监测与故障诊断。发表论文30余篇。E-mail:mzysu@ysu.edu.cn。李 晶,女,1990年生。燕山大学电气工程学院博士研究生。龙海峰,男,1979年生。北京精密机电控制设备研究所高级工程师。潘作舟,男,1994年生。燕山大学电气工程学院硕士研究生。

