一种产品退化试验的仿真与优化方法
方 峻 魏 星 赵森森
1.南京理工大学机械工程学院,南京,210094 2.南京理工大学紫金学院,南京,210046
一种产品退化试验的仿真与优化方法
方 峻1魏 星2赵森森1
1.南京理工大学机械工程学院,南京,210094 2.南京理工大学紫金学院,南京,210046
提出了一种基于性能退化模拟数据的退化试验参数优化方法,该方法适用于已知失效机理并可建立退化数据预测模型的情况。首先采用Bootstrap法建立了可靠寿命置信区间预测模型;然后以可靠寿命置信区间最小为目标,以试验预算费用为约束建立了试验参数的优化模型;接着以某型号武器身管为例,分析了生成模拟退化数据的一般方法,并对身管的退化试验参数进行了优化设计;最后探讨了仿真与优化效果的验证分析方法,通过对相应算例的分析证明了该方法的有效性。
退化试验; 模拟退化数据; 可靠寿命; 身管
0 引言
对于寿命周期较长、试验费用相对昂贵的机械产品(或零部件),基于性能退化数据的分析方法是一种寿命评估和可靠性分析的有效方法。许多机械产品都具有逐渐退化失效的特征,其失效机理主要有疲劳、磨损、烧蚀或化学腐蚀等。很多失效机理都是可以建立相应的理论模型的,如疲劳失效有疲劳累积损伤模型[1],磨损机理有LEE等[2]提出的磨损计算模型,烧蚀则有传热学模型[3-4]等。许多情况下,可以通过理论或经验公式结合仿真的方法估算出主要退化量或与退化相关的性能参数,建立产品的理论退化模型,得出其退化量(如磨损量、疲劳损伤或疲劳裂纹、烧蚀量)或相关性能参数值随工作时间的变化规律,然后通过退化量的失效阈值预测产品的寿命或可靠度。然而,对于新产品的试制样机,为了得到更准确的寿命和可靠性分析结果,通常需要直接采用性能试验中测得的退化数据来进行分析。
为考核产品的性能,退化数据通常来源于性能退化试验的实测数据,如何能够在试验资源有限的条件下获得较准确的可靠寿命预测结果,是退化试验设计需要解决的一个重要问题。对于大多数机械产品来说,不同的工况条件下,其使用寿命也各有差异。为保证预测结果的精度,需要针对具体工况进行退化过程模拟,并采用优化方法来确定投入退化试验的样品的数量、退化试验的试验终止时间、监测退化量的间隔时间单元数等参数。在退化试验之前,基于退化过程模拟得到的退化数据是进行退化试验优化的一个重要参考依据。文献[5-8]基于事先进行的退化试验中获得的退化数据,采用某种退化模型,提出了以分位寿命方差最小为目标的优化方法,存在的主要问题是对于不同的退化模型和服从不同分布类型的模型参数,方差的解析解通常很复杂,推导困难。本文提出了一种具有更广泛适应性的基于Bootstrap法的可靠寿命置信区间优化模型,可以在满足试验费用约束的条件下,进行退化试验相关参数的优化。
1 退化试验仿真与优化的一般流程
在产品设计阶段,通常缺少产品的性能退化实测数据,因此,本文提出的方法首先从产品的失效机理开始研究,采用仿真和理论计算法获得随时间变化的性能退化量。在这里可以采用随机抽样方法,假设结构、材料或载荷参数是服从某一概率分布(如正态分布)的随机数,采用蒙特卡罗方法进行N次抽样,利用不同失效机理的物理模型和计算方法,模拟得到N个样品的性能退化量随时间(或使用次数)变化的数据(表1)。表中v(ik,j)表示发射了ik发时第j个样品的初速。

表1 试验样品退化数据表Tab.1 The degradation data of test samples
在产品试制阶段,可以在这些模拟的退化数据的基础上进行退化试验参数的优化,利用优化后的试验参数进行性能退化试验,从而能在试验预算范围内更准确地评估产品的可靠寿命。退化试验仿真与优化的一般流程和应用方式如图1所示。

图1 退化试验仿真与优化的一般流程和应用方式Fig.1 The general process and application of the simulation and optimization method of the degradation test
2 退化模型及可靠寿命估计
产品的退化过程可以通过某个退化参数的值随时间的变化规律来表示。假设样品的数目为N,可以通过试验测量或进行失效机理的计算机模拟来获得不同时刻的主要性能参数的数值。如表1所示,测量的最小时间单元(或使用次数)为k,即每隔时间k对N个样品的性能退化量进行一次测量,ik时刻第j个样品的退化量为v(ik,j)。
为了确定退化试验的相关参数,首先需要建立退化模型,即退化参数和时间之间的函数关系。本文采用一种常见的线性退化模型来表达退化参数值的变化,其他常见的非线性退化模型也都可以转化为这种线性模型[9]。线性退化模型表达式如下:
vi(t)=βit+αi+εi(t)i=1,2,…,N
(1)
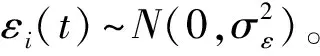
对于其他非线性退化模型,如指数退化模型vi(t)=θ+aieβit+εi(t),也可以转化为线性退化模型来处理。令Ui(t)=ln(vi(t)-θ),αi=lnai,则可以转化为形同式(1)的线性退化模型:
Ui(t)=βit+αi+εi(t)
(2)
对于退化数据更服从哪种退化模型,可以采用统计回归分析的拟合优度检验方法来判定。以下主要针对线性退化模型展开研究。
对于每一个样品来说,其αi和βi的估计值可以通过回归分析的最小二乘原理得出。对于N个样品来说,α和β的均值和标准差的估计值可以通过极大似然法得出。
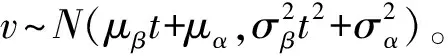
(3)
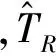
3 优化问题的数学模型
在采用实际退化试验数据分析时,如果采用表1中记录的各时刻的所有数据,并采用最大的样本数量,并不一定能获得最高的预测精度。这是因为实际退化数据与假设的退化模型有一个允许的误差范围,选择最匹配的数据才能使退化模型的误差最小;同时试验样品的数量也不可能很大,在小范围内增大试验样品数并不一定能提高预测精度。实际情况是由于试验费用预算的限制,不可能允许有很多试验样品或进行长时间的退化试验。因此,在退化试验设计时,通常要确定三个主要参数,即参与试验的样品数量n0、退化量监测次数m和监测间隔时间单元f。对于特定的退化数据来说,n0、m和f的数值有个优化的取值范围,可以获得更加精确的可靠寿命估计。另一方面,在试验费用固定情况下,同时又要求获得准确的可靠寿命估计值,故只有通过对试验参数进行优化来确定合适的(n0,m,f)参数组合。优化目标是可靠寿命评估结果的精度最高,这可以采用某一置信水平下的可靠寿命的置信区间宽度来反映,在同一个置信水平下,置信区间宽度越小,预测精度越高。
3.1 基于Bootstrap法的可靠寿命置信区间分析
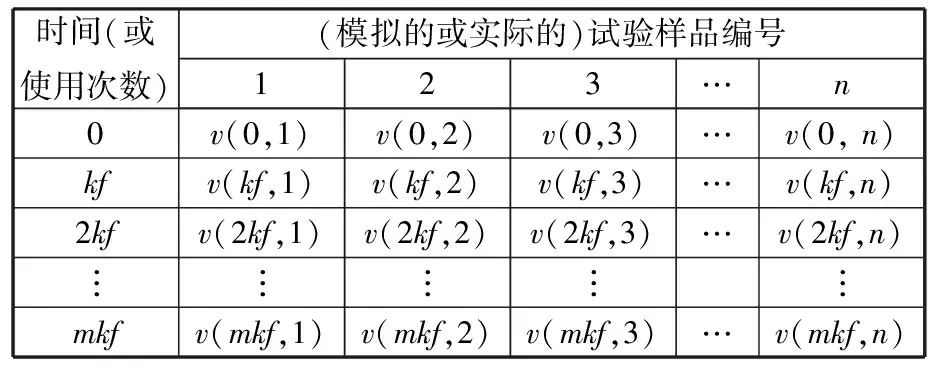
表2 抽取的退化数据Tab.2 The extraction of the degradation data
具体步骤如下:
(1)根据表2的数据,对于每一个样品,根据式(1)的线性退化模型,采用回归分析的最小二乘法估计出退化模型参数αi和βi的值。n个样品共有n个αi和βi的值,即i=1,2,…,n。

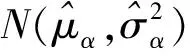
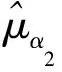


(4)
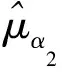
(5)

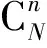
3.2 优化问题的约束条件
确定约束条件为总的试验费用预算不得超出某一值,并且总时间不超过表1中的模拟数据的总时间,即
(6)
n,m,f∈N
其中,cS为单位样品的费用,cm为每次测量的费用,ce为单位时间的费用,ct为总的试验费用预算。由于n、m、f的取值有一定的限定范围,当范围较小时可以采用枚举法获取优化解,范围较大时采用遗传算法进行优化。
4 身管退化试验仿真与优化的算例
身管是火炮和自动武器的一个重要零部件,对身管的寿命进行预测是评价武器性能和改进设计的重要依据。在武器发射过程中,身管内壁会受到高温高压气体的烧蚀和冲击破坏[11],同时也会受到弹丸的挤压和磨损,随着射弹量的增加,身管内膛的径向烧蚀量会逐渐增大,弹丸启动压力下降,身管的发射初速则会呈现逐渐下降的趋势。因此,研究这些退化特征量和射弹数的关系,就可以根据退化特征量的失效阈值,预测其寿命(射弹量)。
内膛烧蚀磨损是身管的主要失效机理,但考虑到弹丸初速的退化趋势比较明显而且易于监测,本文首选弹丸初速作为身管的主要退化参数。在射击过程中,发射初速的数据通常是在试验中实际测量得到的。退化试验的优化需要在已有退化数据的基础上进行,但在制订退化试验方案时,往往没有退化数据,因此需要采用理论(或经验)公式结合数值模拟的方法来获取退化数据。初速的变化可以通过烧蚀量引起的内径的变化来获取,为计算烧蚀量,可以采用熔化烧蚀层理论[3-4]推导出身管膛线起始位置的每一发的烧蚀量,从而得出随射弹量变化的退化数据。身管发射初速退化数据模拟的简要步骤如下:
(1)针对试验武器身管的射击规范(试验标准的射击方式),建立基于身管温度场的有限元仿真模型[12],采用有限元分析软件计算出单发和连续射击k发情况下的膛壁温度场分布和危险截面的最高温度Tw[13]。
(2)采用熔化烧蚀层理论公式[3-4]计算危险截面(膛线起始位置)的累积烧蚀量WSk,得到累积烧蚀量WSk和射弹发数k之间的关系。
(3)身管内膛烧蚀量越大,弹丸的启动压力将越小,将每发烧蚀后的身管内径代入弹丸启动压力计算公式和内弹道方程组[11],就可以计算出弹丸的启动压力和不同射弹量下的发射初速。
(4)将火药气体的温度、火药气体强迫对流系数、材料参数等作为服从正态分布的随机变量,采用随机有限元仿真方法,进行N次抽样(N=500),将得到N个烧蚀量[14]。重复步骤(1)~步骤(3),可得到N个身管的初速退化数据,如表1所示。武器试验的射击规范通常以射击周期(单元)为基础循环重复进行。一个射击周期通常有k发(包含若干个点射或连发)。因此只需记录一个射击周期结束时的弹丸初速。
本算例以某型号速射武器的身管为例进行分析和验证,按照武器性能试验的某种标准的射击规范进行模拟。图2是根据初速模拟退化数据生成的弹丸初速散点图。
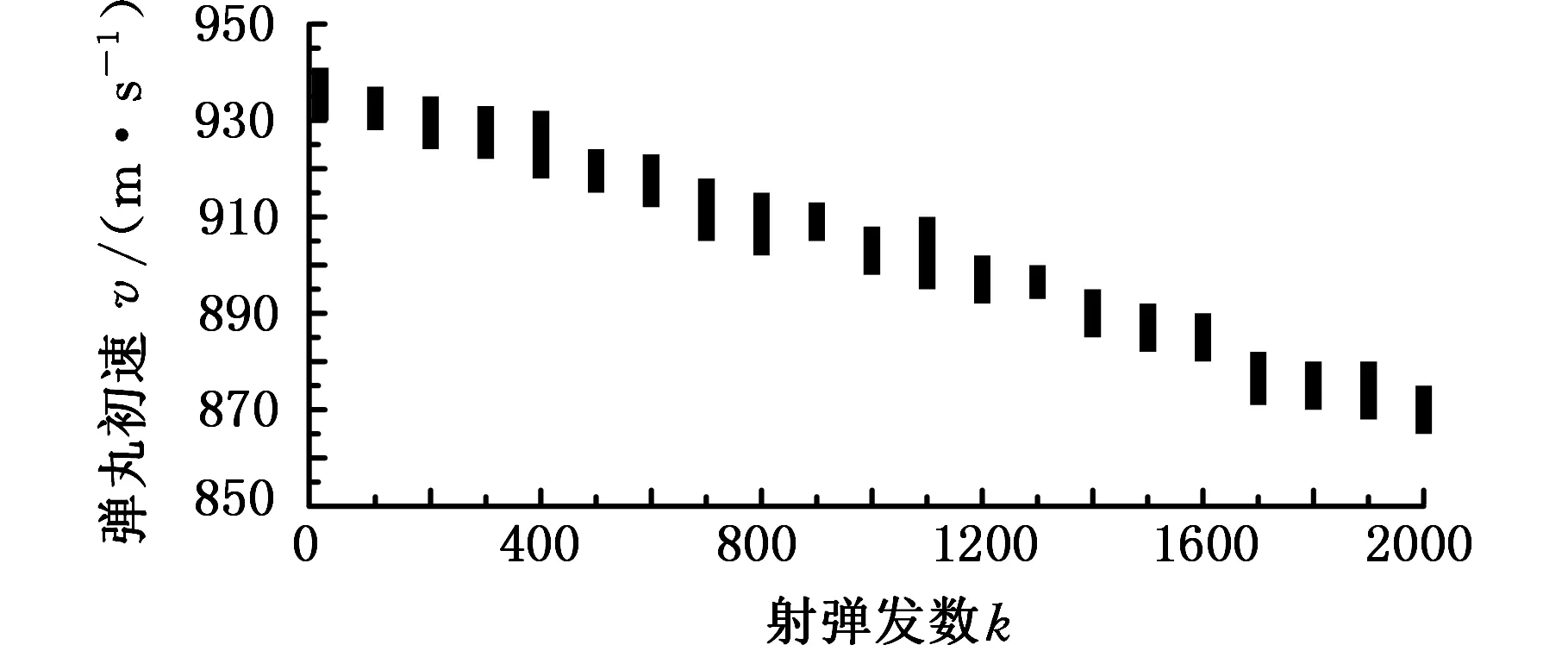
图2 模拟初速的散点图Fig.2 The scatter graph of the simulated initial velocity
在生成N个模拟样品的初速退化数据后,就可以根据此数据进行退化试验参数的优化。采用遗传算法进行优化时,优化目标的计算采用3.1节的可靠寿命置信区间分析方法,并将bootstrap置信区间估计值进行纠偏处理,每次计算优化目标时,从N个模拟样品中按基因编码规则形成不同的(n,m,f)组合,据此产生表2的数据,并定义一个射击周期(单元)为k=20发,射弹3000发时共经历p=150个射击周期。规定发射初速失效阈值为理论初速的88%。
假设试验费用(cs,cm,ce,ct)=(150 000,30,20,1000 000)(元),代入式(6)建立约束条件。对于超过试验预算的值使用惩罚函数将其目标函数值提高,优化目标为函数值最小。
为加快优化速度,取计算置信区间ITR时抽样次数M=1000。由于变量搜索区间较小,可以采用枚举法对目标函数值进行比较和排序,变量搜索区间和优化结果如表3所示。
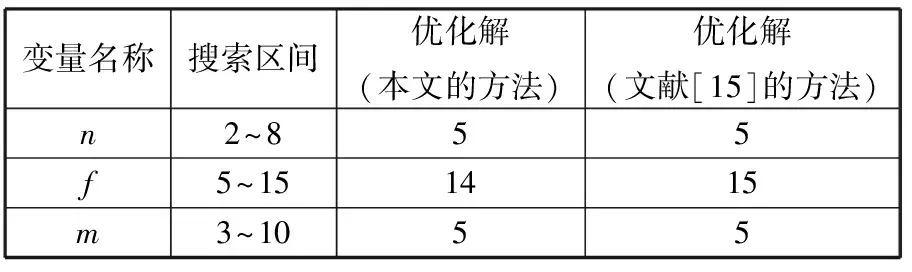
表3 变量搜索区间与优化解
由表3可知,在不超过试验费用预算的情况下,使用5个样品,监测5次,每隔14×20=240发能够获得较准确的寿命估计值。取目标可靠度为0.95,可靠寿命的点估计值为4581发,可靠寿命置信区间为[4347, 4853],置信区间宽度的最小值为506,此时的试验费用为892 100元,试验终止时间为5×14×20=1400(发)。
为便于比较分析,在同样的退化数据基础上,采用文献[5]和文献[15]的方法,推导出可靠寿命(或分位寿命)方差的表达式[15],以可靠寿命方差最小为优化目标,优化变量、搜索区间和优化算法都不变,则优化解见表3,试验终止数量为1500发。两者的计算结果比较接近,但本文的方法克服了寿命方差表达式难以推导的问题,可适用于多种退化模型和寿命分布类型,因此具有更广泛的适用性。
5 仿真与优化效果验证分析
以上通过身管初速退化过程的模拟来确定优化的试验参数,由于设计、制造和使用环境等各方面原因,实测的试验样品退化数据必然与模拟数据具有一定的差异。为了便于对比,按以上算例的射击规范,采用5个身管的实测初速退化数据进行分析。为了保证预测置信区间的准确性和优化方案的合理性,需要验证以下两方面内容:

(7)
给定的显著性水平α下,若F≥F1-α(1,m-2),则回归效果显著,实际的退化数据符合理论退化模型。以上算例的实测初速的部分统计结果见表4。结果表明:减小监测间隔单元数f,增大监测次数m会使实测的退化数据更符合理论模型。这也从另一方面反映了采用线性效应模型来描述身管初速退化数据是合理的。
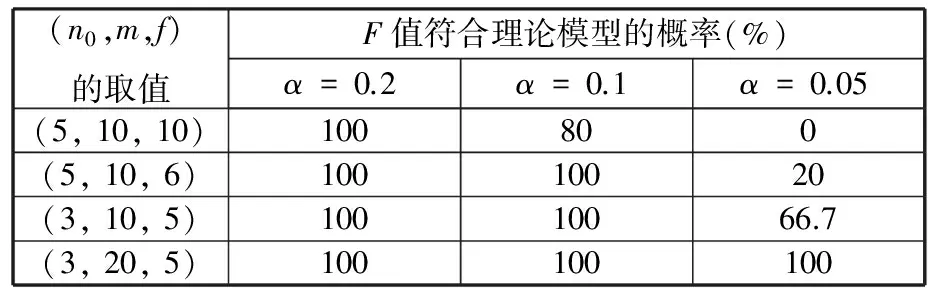
表4 实测初速的部分统计结果Tab.4 The partial statistical results of measured initial velocity from experiment

针对以上算例,采用表3的(n0,m,f)搜索区间,取样品数量n=5,按以上方法计算置信区间覆盖率,绘制出图3所示曲线。结果表明:随着射弹量的增大,基于模拟数据的可靠寿命置信区间将逐渐减小,当射弹量达到一定数量后,置信区间覆盖率将迅速下降,然后不能覆盖基于试验数据的可靠寿命预测值。这是因为随着射弹量的增大,初速模拟数据与试验数据的累积误差逐渐增大,基于模拟数据的置信区间预测结果将不准确。这说明采用模拟数据进行置信区间分析时不宜采用较大的射弹量。

图3 不同射弹量下的模拟数据置信区间覆盖率Fig.3 The coverage of confidence interval from simulation data under different amount of projectile
图4反映了在n和f确定(n=5,f=5)的条件下,监测次数m的变化对可靠寿命置信区间宽度的影响。通过对比模拟数据与试验数据的置信区间的分析结果,发现这两种数据分析得出的置信区间宽度的变化规律基本一致,因此基于模拟数据的试验优化结果仍是可信的。

图4 可靠寿命置信区间宽度变化趋势Fig.4 The variation trend of the width of reliable life confidence interval
6 结束语
本文提出了一种采用模拟退化数据来进行退化试验优化的方法,并建立了一种具有广泛适用性的Bootstrap可靠寿命置信区间优化模型。同时以某型号武器身管的模拟退化数据为例,进行了退化试验参数的优化,并以实际试验数据进行了仿真与优化效果的验证分析,分析结果表明了这种基于仿真的退化试验优化方法是可行的。该方法的优点在于在产品试验之前对性能退化数据进行仿真,可以确定适用于不同工况条件的优化的试验参数。本文的方法主要适用于已知失效机理,并可建立性能退化数据的理论或仿真计算模型的情况;对于无法采用理论或仿真方法预测退化量的情况,则也可以采用以往相同工况条件下的类似型号产品(或零部件)的性能退化试验数据,按本文的方法进行优化,前提条件是两者的退化轨迹(或退化模型)接近。
[1] LEE K O, BAE K H, LEE S B. Comparison of Prediction Methods for Low-cycle Fatigue Life of HIP Superalloys at Elevated Temperatures for Turbo Pump Reliability[J]. Materials Science and Engineering A,2009,519:112-120.
[2] LEE R S, JOU J L. Application of Numerical Simulation for Wear Analysis of Warm Forging Die[J]. Journal of Materials Processing Technology,2003,140:43-48.
[3] 吴斌,夏伟,汤勇,等. 身管熔化烧蚀的预测数学模型[J].火炮发射与控制学报, 2002(1):5-10. WU Bin, XIA Wei, TANG Yong, et al. Mathematical Model for Predicting Melterossion in Gun Barrels[J]. Gun Launch & Control Journal,2002(1):5-10.
[4] LAWTON B. Thermo-chemical Erosion in Gun Barrels[J]. Wear,2001,251(10), 827-838.
[5] WU Shuoye, CHANG Chuntao. Optimal Design of Degradation Tests in Presence of Cost Constraint[J]. Reliability Engineering and System Safety,2002,76(2):109-115.
[6] YU H F, TEENG S T. Designing a Degradation Experiment with a Reciprocal Weibull Degradation Rate[J].Quality Technology & Quantitative Management,2004,1(1):47-63.
[7] WANG Huan, WANG Guanjun, DUAN Fengjun. Planning of Step-stress Accelerated Degradation Test Based on the Inverse Gaussian Process[J].Reliability Engineering and System Safety,2016,154(10):97-105.
[8] HU C H, LEE M Y, TANG J. Optimum Step-stress Accelerated Degradation Test for Wiener Degradation Process under Constraints[J].Europen Journal of Operational Research,2015,241(2):412-421.
[9] GEBRAEEL N. Sensory-updated Residual Life Distributions for Components with Exponential Degradation Patterns[J]. IEEE Transactions on Automation Science and Engineering,2006,3(4):382-393.
[10] DAVISON A C.HINKLEY D V.Bootstrap Methods and Their Application[M].London:Cambridge University Press,1997:3-70.
[11] 张喜发,卢兴华. 火炮烧蚀内弹道学[M]. 北京:国防工业出版社,2001:193-195. ZHANG Xifa, LU Xinghua. The Artillery Ballistics in Ablation [M]. Beijing: National Defense Industry Press,2001:193-195.
[12] ABDULLAH S, HALIL I, CELAL E. Thermo-mechanically Coupled Thermal and Stress Analysis of Interior Ballistics Problem[J]. International Journal of Thermal Sciences,2016,104:39-53.
[13] 吴永海,徐诚,李峰,等. 承受热冲击的大口径机枪枪管的热效应分析[J].南京理工大学学报,2007,31(1):1-5. WU Yonghai,XU Cheng,LI Feng,et al. Thermal Effect of Large Calibre Machine-gun Barrel Sujected to Thermal Shock[J]. Journal of Nanjing University of Science and Technology,2007,31(1):1-5.
[14] ZHOU Wei, FANG Jun. Probabilistic Analysis of Gun Barrel Ablation Life Based on the Modified Response Surface Model[C]//The 4th International Conference on Advanced Engineering Materials and Technology. Xiamen,2013:1076-1083.
[15] 郭志刚, 方峻, 樊黎霞. 基于遗传算法的退化试验优化设计[J]. 机械设计与制造,2011(7):1-3. GUO Zhigang,FANG Jun,FAN Lixia. Optimal Design of the Degradation Tests Based on Genetic Algorithm[J]. Machinery Design & Manufacture,2011(7):1-3.
(编辑 袁兴玲)
A Simulation and Optimization Method of Product Degradation Tests
FANG Jun1WEI Xing2ZHAO Sensen1
1.School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing,210094 2. Zijin College, Nanjing University of Science and Technology, Nanjing,210046
Based on the simulated degradation data, a degradation test optimization method was proposed, which was applicable in the case of known failure mechanism and predicable degradation data. Firstly, the prediction model for confidence interval of the reliable life was built based on the Bootstrap method, and the optimization model for the degradation tests was established, which took the minimum confidence interval of reliable life as the optimization objective, and the experimental costs as the constraints. Then, as an example, the general method of generating simulated degradation data for a certain kind of gun barrel was presented, and the degradation test parameters were designed and optimized. Finally, the verification method of the simulation and optimization results was discussed, and the related examples were analyzed to prove the effectiveness of the method.
degradation test; simulated degradation data; reliable life; gun barrel
2016-05-20
总装备部“十二五”国防预研项目( 51319020202)
TB114.3;TJ01
10.3969/j.issn.1004-132X.2017.07.004
方 峻,男,1974年生。南京理工大学机械工程学院副研究员。主要研究方向为机械可靠性工程、智能设计/制造等。发表论文20余篇。E-mail:13813872656@139.com。魏 星,女,1980年生。南京理工大学紫金学院讲师。赵森森,男,1993年生。南京理工大学机械工程学院硕士研究生。

