例谈“去顶点法”处理三视图问题

筅湖北省武汉市东湖中学冯炜

例谈“去顶点法”处理三视图问题

筅湖北省武汉市东湖中学冯炜

几何体的三视图从本质上来说，是将一个几何体放在某个对应的长（正）方体中，再分别投影到该长（正）方体的里面、右侧面和下底面后，所形成的三个平面图形（其中，侧视图还要将其向右翻折）.因此对于较复杂的三视图还原出对应几何体的问题，可将其放到相应的长（正）方体中进行考查，根据题目中给出的三（正、侧、俯）视图，然后通过排除长（正）方体的顶点——“去顶点法”，可以快捷地确定原几何体的形状，进而解决相关问题.

例1（1）如图1，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长棱的长度为（）.

图1

（2）一个几何体的三视图如图2所示，则该几何体的全面积为（）.

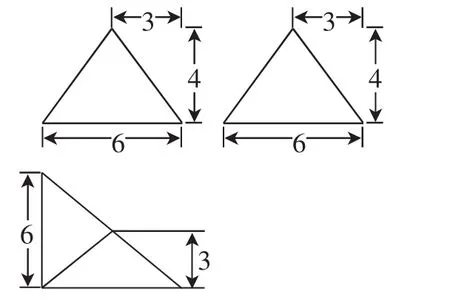
图2

（3）一个几何体的三视图如图3所示，则该几何体的各面面积中的最大值为（）.

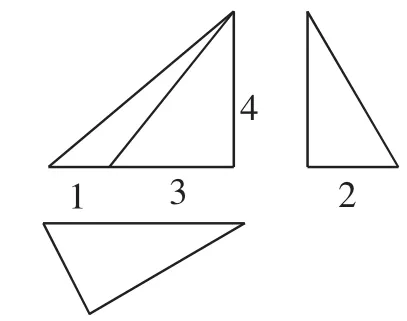
图3

图4

解：（1）如图4所示，作一棱长为4的正方体.由正视图知，顶点A、D应去掉；又由俯视图知，顶点A1应去掉；再由侧视图知，顶点B、B1应去掉.由于正视图中含有高的中点且为实线，从而应有棱BB1的中点E，这样一来可确定原几何体为D1-ECC1.其中，D1C1=CC1=4，D1C=4=6，故最长棱的长度为D1E=6，故应选B.

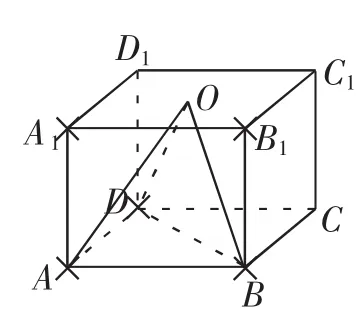
图5

（2）如图5所示，作一长、宽、高分别为6、6、4的长方体.由正视图和侧视图知，顶点A1、B1、C1、D1应去掉；又由俯视图知，顶点C应去掉；再由正视图和侧视图知，应有上底面的中心O，从而可知原几何体为三棱锥O-ABD.其中，AB=AD=6，BD=6，OA=OB=OD=.从而可求得三棱锥O-ABD的全面积为48+12应选A.

（3）如图6所示，作一棱长为4的正方体.由正视图知，点A1、D1应去掉；由侧视图知，点A、B、A1、B1应去掉；结合俯视图知，所对应的几何体为三棱锥E-DCC1，其面积最大的侧面为三角形DCC1，易求得其面积为8，应选B.

图6

例2（1）一个几何体的三视图如图7所示，则该几何体的体积为（）.

图7

（2）图8是某几何体的三视图，则该几何体的体积为（）.

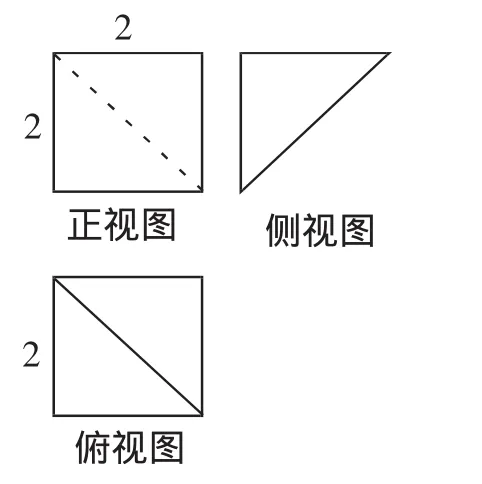
图8

图9

图10

（2）作棱长为2的正方体ABCD-A1B1C1D1.由侧视图可去掉点A、B；当有点C1时，正视图中就没有虚对角线，故应去掉点C1.结合正、侧和俯视图可得原几何体为四棱锥D1-A1B1CD，如图10，故V故应选A.

例3（1）某几何体的三视图如图11所示，则该几何体的体积为（）.

图11

图12

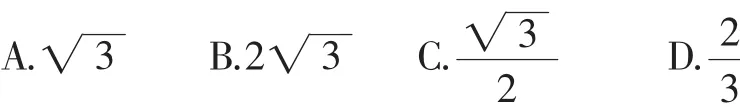
解：（1）作棱长为2的正方体ABCD-A1B1C1D1.由正视图可去掉点B1、C1；由侧视图（注意，要向右翻折），可去掉点C1、D1、C、D.结合正、侧和俯视图可得原几何体为四棱锥A1-ABEF，其中E、F分别为CC1、DD1的中点，如图13，易求得其体积为.故应选B.

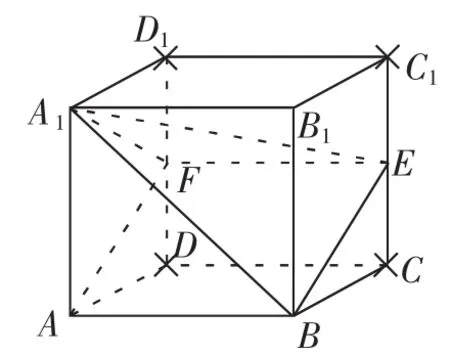
图13

图14

另外对于一些三视图没有全部给出的问题，也可以通过构造对应的正（长）方体来处理.

例4（1）在如图15所示的空间直角坐标系中，一个四面体的顶点坐标分别是（0，0，2），（2，2，0），（1，2，1），（2，2，2），给出编号①、②、③、④的四个图，则该四面体的正视图和俯视图分别为（）.

图15

A.①和② B.③和①

C.④和③ D.④和②

图16

解：（1）如图16所示，作一正方体并建立对应的空间直角坐标系，作出题中对应的点，则易知应选D.

设该长方体的长、宽、高分别为x、y、z，

综上所述，处理与三视图有关的问题时，要用好其对应的长（正）方体这个模型，同时要注意三视图中各线段的虚实对几何体还原的影响.只要熟练、准确地掌握了上述方法，处理此类问题就会得心应手了.