空间几何体体积的求解策略

筅浙江省余姚中学顾丹杰

空间几何体体积的求解策略

筅浙江省余姚中学顾丹杰

空间几何体体积的计算是常见的题型，常见的求解策略有：直接法、等体积法、分割法、补形（体）法等，下面举例说明.

一、直接法

例1如图1所示，在多面体P-ABCD中，平面PAD⊥平面ABCD，AB∥DC，△PAD是等边三角形，已知BD=2AD= 8，AB=2DC=4.求四棱锥P-ABCD的体积.

图1

分析：因为平面PAD⊥平面ABCD，所以考虑在平面PAD内作四棱锥的高，然后再计算底面积，这两个元素确定了，求体积也就顺理成章了.

解：过P作PO⊥AD于O，因为平面PAD⊥平面ABCD，所以PO⊥平面ABCD，即PO为四棱锥P-ABCD的高.

在底面四边形ABCD中，AB∥DC，AB=2DC，

所以四边形ABCD为梯形.在△ABD中，AD=4，BD= 8，AB=4，所以AD2+BD2=AB2，故AD⊥BD.

评注：求一些规则几何体的体积时，可以根据几何体的特点，利用线面垂直、面面垂直等条件，确定几何体的高，解决本题的关键是确定四棱锥P-ABCD的高.

二、等体积法

例2如图2，正方体ABCD-A1B1C1D1的棱长为1，E、 F分别为线段AA1、B1C上的点，则三棱锥D1-EDF的体积为_______.

分析：若直接求三棱锥D1-EDF的体积，则需要求出△DEF的面积和该三棱锥的高，两者都不易求出，所以求三棱锥D1-EDF的体积，可以转化为求F-DD1E的体积.

解：因为正方体的棱长为1，而且E、F分别是线段AA1、B1C上的点，所以点F到平面DD1E的距离即为正方体的棱长1，

图2

评注：当所给几何体的体积不能直接利用公式求解，利用不同的底面积和高来求体积，所得的体积相等，这就是等体积法.等体积法求三棱锥体积的基本思路是：首先判断三棱锥的形状及其结构特征，然后变换三棱锥的底面同时也变换高，再利用三棱锥的体积公式V=sh求解.

三、分割法

例3如图3所示，在多面体ABCDEF中，已知ABCD是边长为1的正方形，且△ADE，△BCF均为正三角形，EF∥AB，EF=2，求该多面体的体积.

分析：本题所给的多面体无法直接求出体积，可以考虑将其分割为几个规则的锥体或柱体进行计算体积.

解法1：如图4所示，分别过A、B作EF的垂线，垂足分别为G、H，连接DG，CH，则原几何体分割为两个三棱锥和一个直三棱柱.

图3

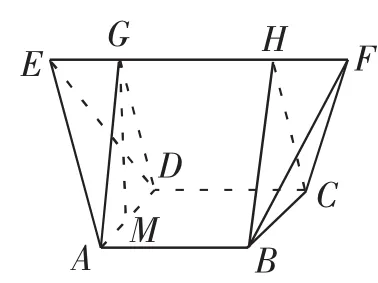
图4

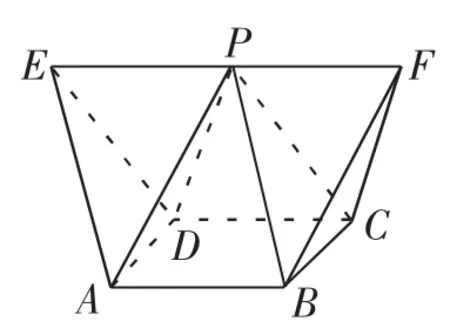
图5

解法2：如图5所示，取EF的中点P，则原几何体分割为两个三棱锥和一个四棱锥，易知三棱锥P-AED和三棱锥P-BCF都是棱长为1的正四面体，四棱锥P-ABCD为棱长为1的正四棱锥.

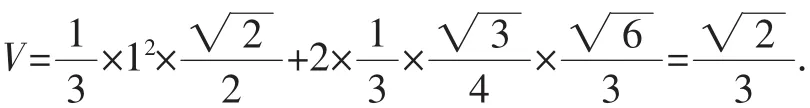
评注：分割法是求一些不规则多面体的常用方法.在具体解题时，要考虑到分割后的椎体或柱体的底面积或高的求解，尽量简化底面积和高的运算.

图6

四、补形（体）法

例4（1）已知某几何体的三视图如图6所示，则该几何体的体积为________.

分析：（1）可利用对称关系，将该几何体补为圆柱，再求体积；（2）若按常规解题思路是求底面积和高，底面积易求，但高不易求.由已知条件中的三组对棱分别相等，可联想到长方体对面不平行的对角线也具有这种性质.从而将此三棱锥补成一个长方体，从而可快捷解决问题.

解：（1）由三视图可知，此几何体是底面半径为1，高为4的圆柱被从母线的中点处截去了圆柱的，根据对称性，可补全此圆柱如图7，故体积V=×π× 12×4=3π.

图7

（2）可将如图8所示的三棱锥补成图9所示的长方体，设AD=a，DB=b，DC=c，故a2+ b2=52，b2+c2=41，a2+c2=34.解得a=3，b=4，c=5.

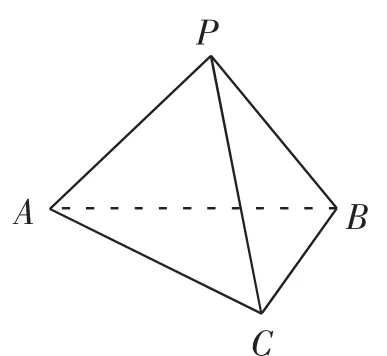
图8

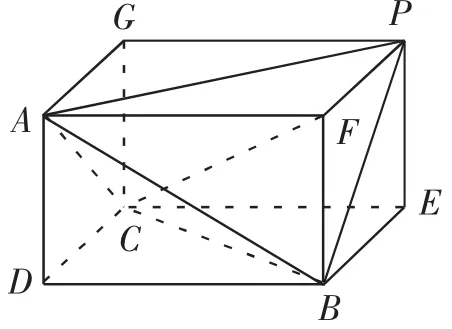
图9

故VP-ABC=VAFPG-DBEC-4VA-BCD=

评注：补形法常见的有两种情况：（1）对称补形求体积：某些不规则的几何体，若存在对称性，则可考虑用对称的方法进行补形，把它们放入一个规则几何体中加以解决.（2）联系补形：某些空间几何体虽然也是规则几何体，不过几何量不易求解，可根据其所具有的特征，联系其他常见几何体，作为这个规则几何体的一部分来求解.三条侧棱两两互相垂直，或一侧棱垂直于底面，底面为正方形或长方形，则此几何体补形为正方体或长方体，使所解决的问题更直观易求.

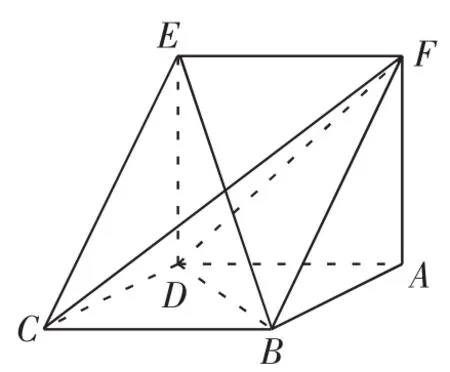
图10

五、函数法

例5如图10，在平行四边形ABCD中，BC=2，BD⊥CD，四边形ADEF为正方形，平面ADEF⊥平面ABCD.记CD=x，V（x）表示四棱锥F-ABCD的体积，求V（x）的最大值.

分析：解答本题的关键是求出V（x）的表达式，然后再根据表达式的特点选择方法求最值.

解：因为平面ADEF⊥平面ABCD，交线为AD且FA⊥AD，

所以FA⊥平面ABCD.

又BD⊥CD，BC=2，CD=x，

所以当x2=2时，即x=时，V（x）取得最大值，且

又0

评注：对于截面周长、面积、体积等的最值问题，常常可以通过构造目标函数转化为函数的最值，同时注意实际问题中的自变量的取值范围.