基于盲数理论的城市土地价格评估方法研究

舒服华 王艳

城市土地价格评估涉及范围广，是一个模糊性和不确定性共存的复杂系统工程，需要借助有效数学工具和先进的评估方法，才能得到客观准确的结果。作者介绍了盲数理论的基本知识和盲数多属性决策的方法与步骤，提出了城市土地价格评价指标体系，运用盲数理论对武汉市某地块价格进行评估，采用模糊一致矩阵确定指标的权重，有效提高了评估的客观性。

土地是人类赖以生存和发展的物质载体，对人类社会和国民经济的发展起着举足轻重的作用。近年来，随着城市人口的不断增加、城市规模的不断扩大和城市化进程的不断加快，土地这一资源变得越来越重要，其稀缺性也日益明显，供求矛盾也越来越突出，价格也在不断攀升。随着我国土地使用制度改革的不断深化，土地价格已成为调节土地供给和需求，促进土地使用权合理流动、合理配置和产生最大效益的重要手段。城市土地价格是地方政府经营城市土地、制定和实施土地供应计划、调控土地供应结构时的重要参考，也是土地市场交易、房地产开发、建设项目投资决策和房地产税制改革的重要依据。但近些年城市土地虚高的价格，可能带动房价恶性上涨，引发物价上涨进而导致通货膨胀，触发金融风险；不利于解决我国城市居民的住房问题；容易滋生腐败；阻碍城市的可持续发展。科学评估土地价格是土地使用制度深化改革的客观需要，它有利于地产经营，有利于实现具有中国特色的社会主义城市土地管理，有利于土地的集约利用，有利于土地市场可持续健康发展。在当前复杂的市场经济条件下，城市土地价格的影响因素具有复杂性，既有客观因素，也有人为因素。城市土地价格评估涉及范围广、领域多，是一个模糊性和不确定性共存的复杂系统工程，只有依靠大家的智慧，借助有效数学工具和先进的评估方法，才能得到客观准确的结果。盲数是一种新的数学方法，用来表达信息的不确定性，这种含有随机性、模糊性、灰性及未确知性两种或两种以上不确定性的信息称为盲信息，能更好地反映客观因素的不确定性，是处理和表达盲信息的有力数学工具。由于盲数理论可以处理至少两种以上的不确定性信息，因此对于多种不确定性共存的复杂系统，具有较好的适用性。文中运用盲数理论评估城市土地价格，能有效提高评价的科学性。

一、盲数的基本知识

未确知信息是有别于随机信息、模糊信息和灰信息的一种不确定信息，它是指由于决策者所掌握的证据尚不足以确定事物的真实状态和数量关系，从而带来的纯主观认识上的不确定性信息。盲数则是未确知数学中表达和处理盲信息的数学工具。

1.盲数的定义：设G为区间型灰色集，xi∈G，ai∈[0，1]，i=1，2，…，n，f(x)为定义在上的灰函数，且f(x)可表示为

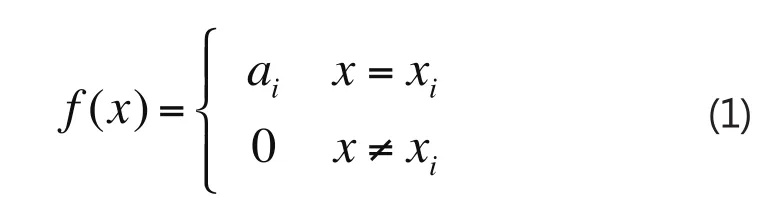
式中，，则称xi为一个盲数，ai为f(x)的xi值的可信度，a为xi的总可信度，n为xi的阶数。

2.盲数的运算：设有A和B两个盲数

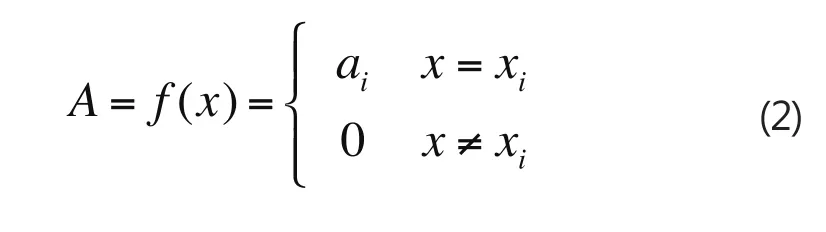
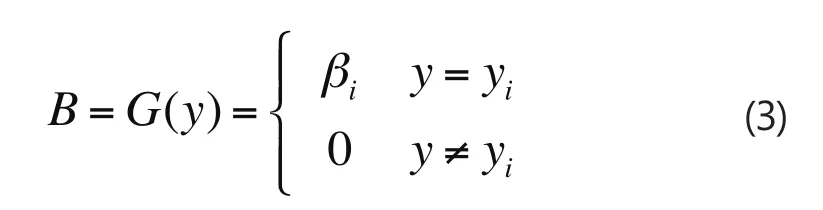
则A和B两个盲数间的运算规则可通过可能值和可信度值两个矩阵来实现。

3.盲数的均值：设a和b为实数，a≤b，称(a+b)/2为有理灰数[a，b]的心，记为Θ(a，b)=(a+b)/2。

设盲数

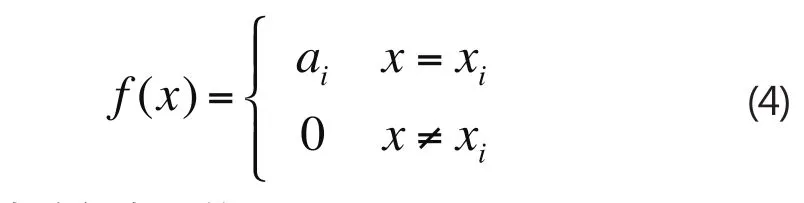
则一阶未确知有理数

为盲数f(x)的均值，其中，Θ为有理灰色xi的心。

4.专家的综合可信度：假设有个专家参与决策，它们的信任度分别为θ1，θ2，…，θk，则专家的综合可信度为

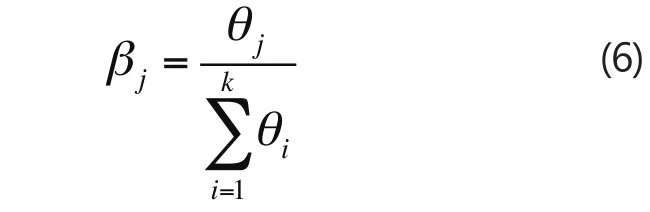
式中，βj为专家j的综合可信度，j=1，2，…，k。

5.可能值区间无交叉划分：设盲数f1(x)的可能值区间[x1，y1]，[x2，y2]，…，[xn，yn]相互交叉，其可信度分别为a1，a2，…，an，将区间序列的端点值由小到大排列，组成新的无交叉区间序列[s1，t1]，[s2，t2]，…，[sn，tn]，则新区间的可信度为

6.盲数的信息融合：设f1 (x)，f2(x)，…，f1m(x)是盲数形式的信息，每条信息的权重为w1，w2，…，wm，则这m条盲数的期望值（均值）为

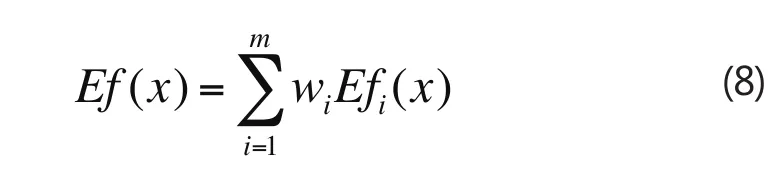
二、盲数理论评价法步骤

1.确定评价指标：影响城市土地价格的因素主要有：（1）一般因素。一般因素是指影响土地价格的一般、普遍、共同的因素，是在一般社会经济方面对土地价格总体水平产生影响，从而成为决定各土地具体价格的基础。（2）区域因素。区域因素是指土地所在地区的自然条件与社会、经济条件。这些条件相互结合所产生的地区特性，对地区的地产价格水平有决定性的影响。（3）个别因素。个别因素是指宗地本身的条件和特征，主要包括面积、宽度、深度、坡度、宗地市政设施条件、城市规划限制、宗地位置、土地使用年限。对于一个城市而言，影响土地价格的直接因素是区域因素和个别因素，区域因素包括土地所处位置的繁华程度、交通条件、基础设施、环境质量，个别因素主要含宗地状况。繁华程度主要指地块距城市中心、商业服务中心或其他人们活动集聚中心的距离及各类中心对城市其他区域的影响程度；交通条件，主要有区域的交通类型、对外联系方式及方便程度、整体性交通结构、道路状况及等级、公共交通状况及路网密度等；基础设施条件，指地块所在地上下水、电力、电讯、煤气、暖气以及幼儿园、学校、公园、医院等设施的等级、结构、保证率、齐备程度及距离等；环境质量，包括地块地质、地势、坡度、风向、空气和噪音污染程度等各种自然环境条件，以及周围居民职业类别、教育程度等人文环境条件；宗地状况主要有地块形状、大小、土地利用性质、用地结构、用地限制条件、区域交通管制、城市规划限制等。故文中选取繁华程度（c1）、交通条件（c2）、基础设施（c3）、环境质量（c4）、宗地状况（c5）5各方面作为城市土地价格评估指标。城市土地评估指标体系如图1所示。

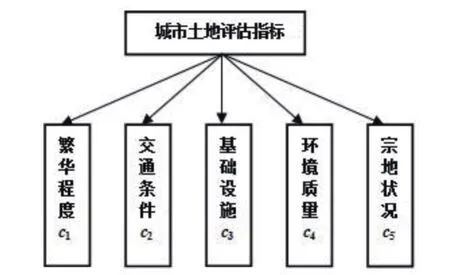
图1 城市土地评估指标体系

2.确定权重集：权重集是表示各个指标在指标体系中重要程度的集合。本文采用改进的层次分析法赋权。由于传统的层次分析法确定权重计算过程复杂，且要进行一致性检验，故采用模糊一致矩阵进行改进，其权重计算简单且不需要一致性检验。基本方法是：首先对属性指标的重要性进行两两比较，然后根据表1所示的0.1-0.9标度法法则确定评分，以此构造优先关系矩阵（互补矩阵）D。

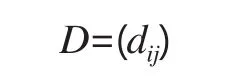
式中，dij为评价指标i相对于评价指标j的得分，其中，dii=0.5；dji=1-dij。

表1 标度值确定法则

根据优先关系矩阵构造模糊一致矩阵：E=(eij)，且eii=0.5；eji=1-eij

式中，，即表示优先关系矩阵按行求和。

根据模糊一致矩阵，求取各评价指标的权重

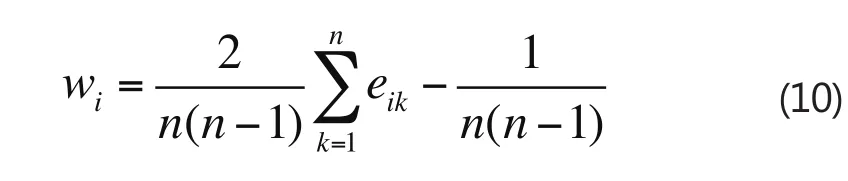
式中，wj第j个评价指标的权重。

3.确定指标的评价值：指标的评价值为评价对象符合评价指标程度的度量。它由专家们根据自己的知识、经验、理解和判断来作出，为了使评估更准确，本文采用多名专家集体评估，且专家给出的评价值为区间灰数，具有一定的不确定性，这样更符合客观实际。

4.计算专家的综合可信度：首先根据专家的权威性、学识、专长给出个体的可信度，然后按式(6)求出各专家的综合可信度。

5.评价值转化为盲数形式：由于专家给出的评价值可能出现交叉现象，需要对专家给出的评价值进行整理，即将评价值进行无交叉区间划分，得到盲数的可能值，然后按照式(7)求划分后可能值对应的可信度，并对可信度进行归一化，转化为规范化盲数信息。根据盲数的性质，按照式(5)计算各评价指标盲数形式的评价值的均值。

6.求评价对象的评价值：本文评价对象的评价值采用均值。当各指标的均值和权重确定后，按照式(7)计算评价对象的最终评价值，也就是土地价格的基准价格。

三、实例分析

以武汉市某区块待出售住宅用地为例，运用盲数理论对该土地的低价进行评估。邀请5位房地产领域专家进行评估， 由于5位专家的知识水平差异，对评估结果的客观性有一定的影响，因此用专家可信度加以修正。设5位专家的可信度分别为θ1=0.9，θ1=0.85，θ1=0.8，θ1=0.75，θ1=0.70，各专家依照土地价格估价指标进行估价，即对该地块繁华程度、交通条件、基础设施、环境质量、宗地状况5个方面的情况进行估价，价格为区间数（灰数），存在一定的不确定性。5位专家对该地块5项指标的估价如表2。

1.求专家的综合可信度

β1=0.9/(0.9+0.85+0.8+0.75+0.7)=0.2250，同理：β2=0.2125，β3=0.2000，β4=0.1875，β4=0.1750。

2.将评价值转化为盲数

由于专家的估价区间有一定的交叉，对每个指标估价区间进行重新划分，使其变为无交叉区间。方法是：首先找出各指标估价的最大最小值，然后将最小最大值组成的区间划分均等的若干小区间，最后求各区间值的可信度，将估价值转化为盲数形式，各指标估值区间可以相同，也可以不同，为了计算方便，本文各指标的区间划分数目相同。

以专家给出的“繁华程度c1”指标估价值为例，最小值为6300，最大值为8400，将区间[6300，8400]等分为4个无交叉的区间，即：[6300，6825]，[6825，7350]，[7350，7875]，[7875，8400]。按照式(7)计算新区间的可信度。

当x∈[6300，6825]时，可信度为

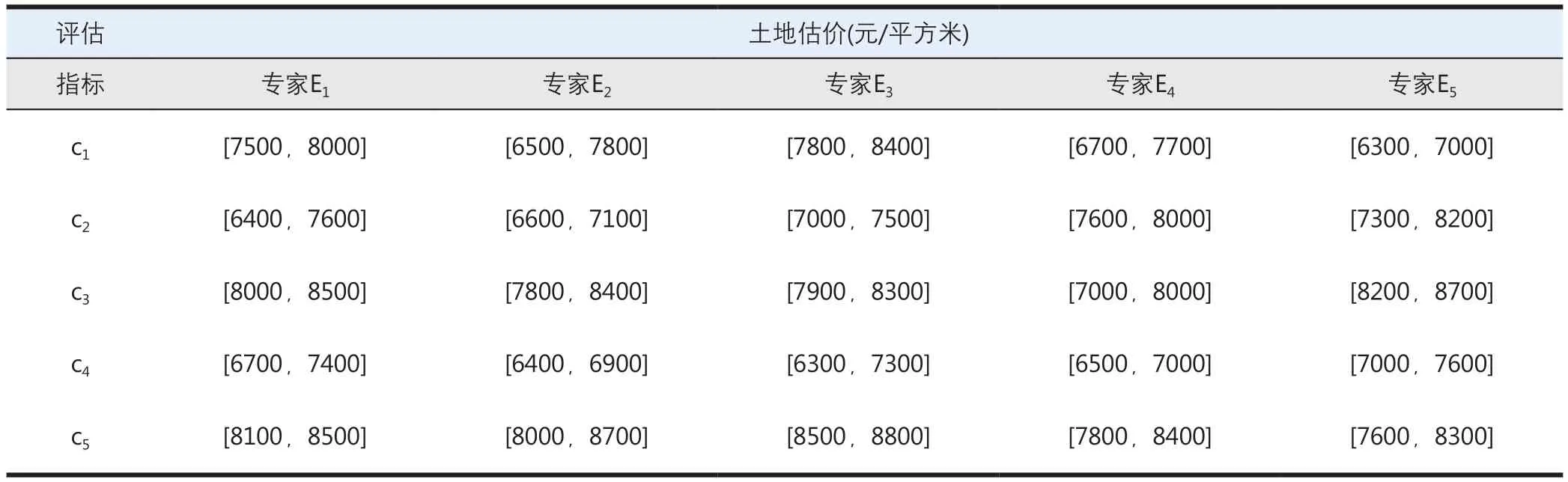
表2 住宅地块专家估价结果

当x∈[6825，7350]时，可信度为

µ1(2)= [(7800-6500)/(8400-6300)]×0.2125+[(7700-6700)/( 8400-6300)]×0.1875=0.8833；

当x∈[7350，7875]时，可信度为

µ1(3)=[(8000-7500)/(8400-6300)] ×0.2250+[(7800-6500)/(8400-6300)] ×0.2125+[(8400-7800)/(8400-6300)]×0.2 =0.9691

当x∈[7875，8400] ]时，可信度为

µ1(4)=[(8000-7500)/(8400-6300)]×0.2250+[(8400-7800)/(8400-6300)]×0.1875 =0.4286

对可信度进行归一化，

α1=1.1162/(1.1162+0.8833+0.9691+0.4286)=0.3286，同理，α2=0.2600，α,3=0.2853，α,4=0.1261。

于是得到指标c1评估值的4阶盲数为

同理，可得到c2、c3、c4、c5的盲数形式的估值，分别为

3.评价指标的权重

根据实际经验和专家意见，土地价格5个评价指标的标度值取为d12=0.7，d13=0.7，d14=0.6，d15=0.6，d23=0.7，d24=0.6，d25=0.6，d34=0.7，d35=0.6，d45=0.6。于是优先关系矩阵为：

则e1=3.1，e2=2.7，e3=2.4， e4=2.2，e5=2.1，e12=0.54，e13=0.57，e14=0.59， e15=0.60，e23=0.53，e24=0.55，e25=0.56，e34=0.52，e35=0.53，e45=0.51；模糊一致矩阵为：

则，同理，求得w2=0.210， w3=0.195，w4=0.185，w5=0.180。

4.求各评价指标评估值的均值

仍然以“繁华程度c1”指标为例，根据盲数 的性质，其数学期望为：

Ef(x1)=(6300+6825)/2×0.3286+(6825+7350)/2×0.2600+(7350+7875)/2×0.2853+(7875+8400)/2×0.1261=7197.17。

同理，可求得其它指标评估值的均值，Ef(x2)=7237.36，Ef(x3)=7782.55，Ef(x4)=6938.50，Ef(x5)=8343.85。

5.求最终评估值

评估对象的最终评估值为单指标评估值的加权平均值，即

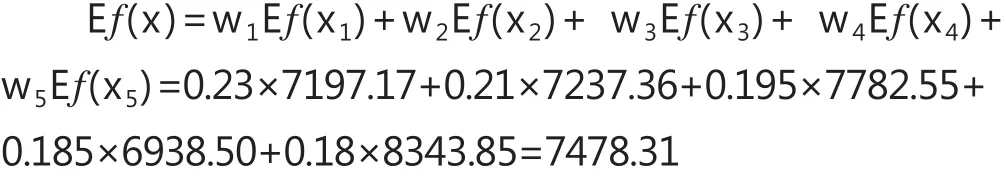
故该地块的最终基本价格为7478.31元/平方米。

四、结语

城镇土地是城镇经济社会发展的物质载体和宝贵的经济资源，是城市经济中的重要资产。随着城市化、工业化进程的加快，人地矛盾日益突出，土地日显稀缺，地价能有力地促进土地资源的合理利用。城市土地市场是我国市场体系的重要组成部分，但当前我国城镇土地市场还不完善，土地价格波动不完全受市场供求规律限制，土地市场价格的波动影响着城市的经营与发展、房地产市场的良性运行乃至国民经济健康持续发展。土地市场健康发育与否对我国城市发展、城市化进程有重要影响。科学评价城市土地价格，对调节土地价格波动，对宏观调控城市土地价格，对促进集约、节约利用土地，科学配置土地资源，促进土地科学管理等具有重要意义。盲数是解决随机性、模糊性、灰性及未确知性等不确定性问题的有力数学工具。文中利用盲数理论城市土地价格，决策者由专家团组成，有利于集中不同领域专家和团队成员的智慧，评价值为灰数，更贴近现实，采用模糊一致矩阵确定指标的权重，有效提高了评价结果的准确性。

[1]李新仓.我国城市土地价格的影响因素及调控对策[J].商业经济研究,2015.(11):43-44.

[2]李博,原玉廷.一种改进的城市土地价格计算方法[J].中国土地科学,2008.22(4):45-48.

[3]尹念辅,李铁松,左云霞.基于盲数理论的四川省西充河水环境容量研究[J].水土保持通报,2012.32(1):233-237.

[4]路石俊,李翔.基于盲数理论的变电站工程全寿命周期成本估算[J].电网技术.2010.34(3):141-145.

[5]唐晓娇,黄瑾辉,李飞.基于盲数理论的水体沉积物重金属污染评价模型[J].环境科学学报, 2012.35(5):1104-1112.

[6]陈剑勇,蔡红梅,苏浩益.盲数理论在发电系统可靠性评估中的应用J].电力系统保护与控制, 2012.40(13):74-77.