一类分数阶Genesio-Tesi系统的滑模混沌同步*
毛北行,李巧利
(1.郑州航空工业管理学院理学院,河南 郑州 450015; 2.河南工业大学理学院,河南 郑州 450001)
一类分数阶Genesio-Tesi系统的滑模混沌同步*
毛北行1,李巧利2
(1.郑州航空工业管理学院理学院,河南 郑州 450015; 2.河南工业大学理学院,河南 郑州 450001)
研究了Genesio-Tesi系统的滑模混沌同步问题,基于Lyapunov稳定性理论及分数阶微积分给出了主从系统取得混沌同步的充分条件,研究表明,在一定条件下,选取适当的控制器Genesio-Tesi系统的主从系统是滑模混沌同步的。
滑模;混沌同步;Genesio-Tesi系统
在传统的控制理论中,通常假设被控对象和控制器模型为整数阶次,然而这样的整数阶系统与实际系统存在一定的差距.Mandelbrot指出在自然界和人类社会存在着大量的分数维系统[1-7],采用分数阶模型能更好的揭示对象的行为和本质。Oustaloup[8]提出了将分数阶控制器用于动态系统的设想,研究和对比分析表明分数阶控制器有更好的鲁棒性等优点。分数阶滑模控制,能够在传统的滑模控制的基础上提高系统的控制性能和精确性,成为现代非线性控制的重要研究方法[9-16]。Genesio-Tesi系统是物理学中典型的混沌系统,该系统具有混沌系统的很多特征,它包含了一个简单的平方项,在文献[17]中Genesio-Tesi混沌系统得到了详细的论述,文献[18]研究了Genesio-Tesi系统的自适应同步问题,文献[19]研究了分数阶Genesio-Tesi系统的混沌同步问题,讨论了阶次相等和阶次不等两种情形。本文研究了一类具有五次方非线性项的整数阶与分数阶Genesio-Tesi系统的滑模混沌同步问题,基于Lyapunov稳定性理论及分数阶微积分给出了主从系统取得混沌同步的充分条件,研究表明,一定条件下,选取适当的控制器Genesio-Tesi系统的主从该系统是滑模混沌同步的。
1 主要结果
以下考虑如下一类五次方非线性项的整数阶Genesio-Tesi混沌系统
(1)
当b1=6,b2=2.29,b3=1.2,b4=-1时,系统出现混沌吸引子,以上述系统为驱动系统,设计响应系统为:
(2)
(3)
定理1 若设计滑模函数
s(t)=b2e1(t)+b3e2(t)+εe3(t),ε>0,
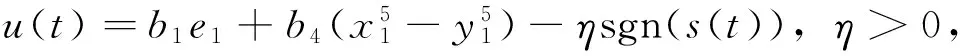
证明s(t)=b2e1(t)+b3e2(t)+εe3(t),
当发生滑模运动时,需满足如下条件
s(t)=b2e1(t)+b3e2(t)+εe3(t)=0
(4)
冷冻保鲜凤尾鱼、食用精盐、太太乐鸡精、白砂糖、太太乐特味鲜调味料、葱粉、姜粉、白胡椒粉、五香粉、风车淀粉、高度白酒、加饭酒、饴糖。
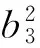
(5)
上述微分方程等价于
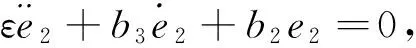
当不在滑模面上运动时,构造Lyapunov函数:
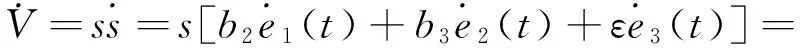
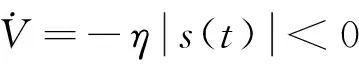
定义1[20] Caputo分数阶导数定义为
n-1<α 以下考虑分数阶Genesio-Tesi混沌系统 (6) b1=2,b2=3.5,b3=0.3,b4=-1,q=0.95时系统呈现混沌态,以上述系统作为驱动系统,设计响应系统为: (7) 定义系统误差ei(t)=yi(t)-xi(t),i=1,2,3,以上两式相减得到误差系统为: (8) 定理2 当0.5 证明 当系统发生滑模运动时,需满足如下条件: (9) ⟹ 当ε>0时,对上式使用拉普拉斯变换得 sqb3E1(s)-b3sq-1e1(0)+b2E1(s)=0 其中E1(s)=L(e1(t)),L表示拉普拉斯算子,根据拉普拉斯终值定理 (10) 由于符号函数的性质: 分数阶Genesio-Tesi混沌系统。 图1 整数阶系统的误差Fig.1 Errors of integer systems 图2 分数阶系统的误差Fig.2 Errors of fractional-order systems 基于Lyapunov稳定性理论及分数阶微积分,研究了一类具有五次方非线性项的整数阶以及分数阶Genesio-Tesi系统的滑模混沌同步问题,给出了主从系统取得滑模混沌同步的充分性条件,数值仿真表明该方法是可行性的。 [1] 丁金凤,张毅. 基于按指数律拓展的分数阶积分的El-Nabulsi-Pfaff变分问题的Noether对称性[J].中山大学学报(自然科学版):2014,54(6):150-154.DINGJF,ZHANGY.NeothersymmetriesforEl-Nabulsi-Pfaffvariationalproblemforextendedexponentialfractionalintegral[J].ActaScientiarumNaturaliumUniversitaltisSunyatseni,2014,53(6):150-154. [2] 金世欣,张毅. 基于Caputo分数阶导数的含时滞的非保守系统动力学的Noether对称性[J].中山大学学报(自然科学版),2015,54(5):24-31.JINSX,ZHANGY.Noethersymmetriesfornon-conservativeLagrangesystemswithtimedelaybasedonCaputofractionalderivative[J].ActaScientiarumNaturaliumUniversitaltisSunyatseni,2015,54(5):49-55. [3]ZHANGY.Fractionaldifferentialequationsofmotionintermsofcombinedriemann-liouvillederivatives[J].ChinesePhysicsB,2012,8(21) : 302-306. [4] 张毅. 相空间中类分数阶Noether对称性与守恒量[J]. 中山大学学报(自然科学版) ,2013,52(4) : 20- 25.ZHANGY.Noethersymmetryandconservedquantityforafractionalactionlikevariationalprobleminphasespace[J].ActaScientiarumNaturaliumUniversitaltisSunyatseni,2013,52(4):45-50. [5]MANDELBROTBB,vanNESSJW.Fractionalbrownianmotions:fractionalnoisesandapplications[J].SIAMReview,1968,10(4):422-437. [6]MANDELBROTBB.Thefractalgeometryofnature[M].NewYork:WHFreeman&CoLtd,1974. [7]BAGLEYRL,TORVIKPJ.Ontheappearanceofthefractionalderivativeinthebehaviorofrealmaterials[J].JApplMech,1984,51(4):294-298. [8]OUSTALOUPA.LaDévirationnonentiere:Théorie,synthéseetapplications[M].Paris:Hermes,1995. [9]SHAHIRIM,GHADRIR,RANJBARN,etal.Chaoticfractional-ordercoulletsystem:synchronizationandcontrolapproach[J].CommunNonlinearSciNumerSimul, 2010,15:665-674. [10]HAMAMMCIKM.Calculationofallstabilizingfractional-orderPDcontrollersforintegratingtimedelaysystems[J].ComputMathAppl,2010,15:1267-1278. [11]MATOUKA.Chaosfeedbackandsynchronizationoffractional-ordermodifiedautonomousVanderpol-Dufflingcircuit[J].CommunNonlinearSciNumerSimul, 2011,16:975-986. [12]MOMAHHADPA.Robustfinite-timestabilizationoffractional-orderchaoticsusyemsbasedonfractionalLyapunovstabilitytheory[J].JournalofComputationandNonlinearDynamics, 2012,7:1011-1015. [13]MILAD,MHD.Synchroni-zationoffractionalorderhyper-chaoticsystemsbasedonanewadaptiveslidingmodecontrol[J].IntJDynamControl,2015,10(7):435-446. [14]DELAVARIH,GHADERIR,RANJBARA,etal.Fuzzyfractionalorderslidingmodecontrollerfornonlinearsystems[J].CommunicationsinNonlinearScienceandNumericalSimulation,2010,15(4):963-978. [15] 毛北行,李巧利.一类分数阶Duffling-Vanderpol系统的混沌同步[J].吉林大学学报(自然科学版),2016,54(2):369-373.MAOBX,LIQL.Chaossynchronizationofaclassoffractional-orderDuffling-Vanderpolsystems[J].JournalofJilinUniversity(NaturnalScienceEdition),2016,54(2):369-373. [16] 王悍枭,刘凌,吴华伟.改进型滑模观测器的永磁同步电机无传感器控制策略[J].西安交通大学学报,2016,50(6):104-109.WANGHN,LIUL,WUHW.Asensorlesspermanentmagnetsyncronousmotorcontrolstrategyforimprovedslidingmodeobserverswithstatorparametersidentification[J].JournalofXianJiaotongUniversity,2016,50(6):104-109. [17]LUJG.Chaoticdynamicsandcynchronizationoffractional-orderGenesio-Tesisystems.[J].ChinesePhysics,2005,14(8):1517-1521. [18] 田现东,卢殿臣.Genesio-Tesi系统的自适应同步控制[J].昆明理工大学学报(理工版),2007,32(6):119-124.TIANXD,LUDC.Self-adaptivesynchronizationcontrolofGenesio-Tesisystem[J].JournalofKunmingUniversityofScienceandTechnology(ScienceandTechnology) 2007,32(6):119-124. [19] 刘晓君,洪灵. 分数阶Genesio-Tesi系统的混沌及自适应同步[J].动力学与控制学报,2016,14(4):318-323.LIUXJ,HONGL.Chaosandadaptivesynchronizationinfractional-orderGenesio-Tesisystems[J].JournalofDynamicsandControl, 2016,14(4):318-323. [20]PODLB.Fractionaldifferentialequation[M].SanDiego,CA,USA:AcademicPress, 1999:715-719. Sliding mode chaos synchronization of a class of fractional-order Genesio-Tesi systems MAOBeixing1,LIQiaoli2 (1.College of Science, Zhengzhou Institute of Aeronautical Industry Management, Zhengzhou 450015, China; 2.College of Science, Henan University of Technology, Zhengzhou 450001,China) The sliding mode chaos synchronization problem of Genesio-Tesi systems using is studied based on Lyapunov stability theory and fractional-order caculurs. The sufficient conditions for the master-slave systems realized chaos synchronization are concluded. The study illustrated that emotion models are sliding mode chaos synchronization under certain conditions choosing proper controller. sliding mode; chaos synchronization ; Genesio-Tesi systems 2016-09-28 基金项目:国家自然科学青年基金(NSFC11501525);河南省科技厅软科学项目(142400411192);河南省高等学校青年骨干教师资助计划项目(2013GGJS-142) 毛北行 (1976年生),男;研究方向:复杂网络与混沌同步;E-mail:bxmao329@163.com 10.13471/j.cnki.acta.snus.2017.02.013 O A 0529-6579(2017)02-0076-04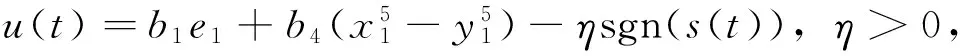
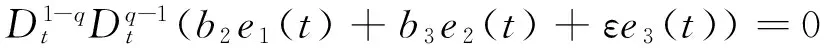


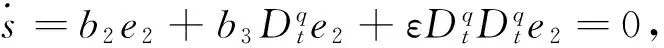
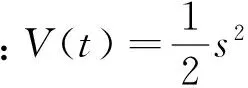
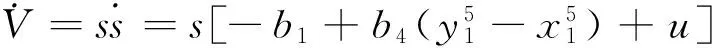
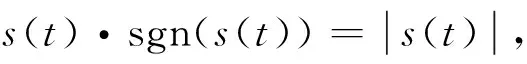
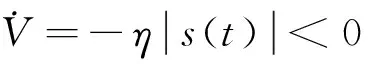
2 数值仿真

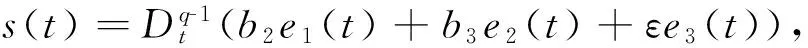
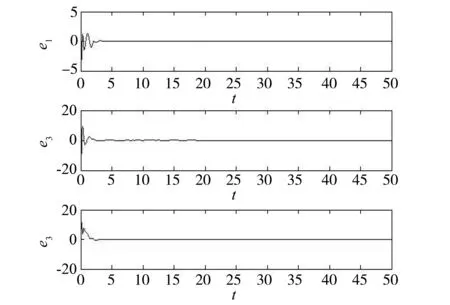
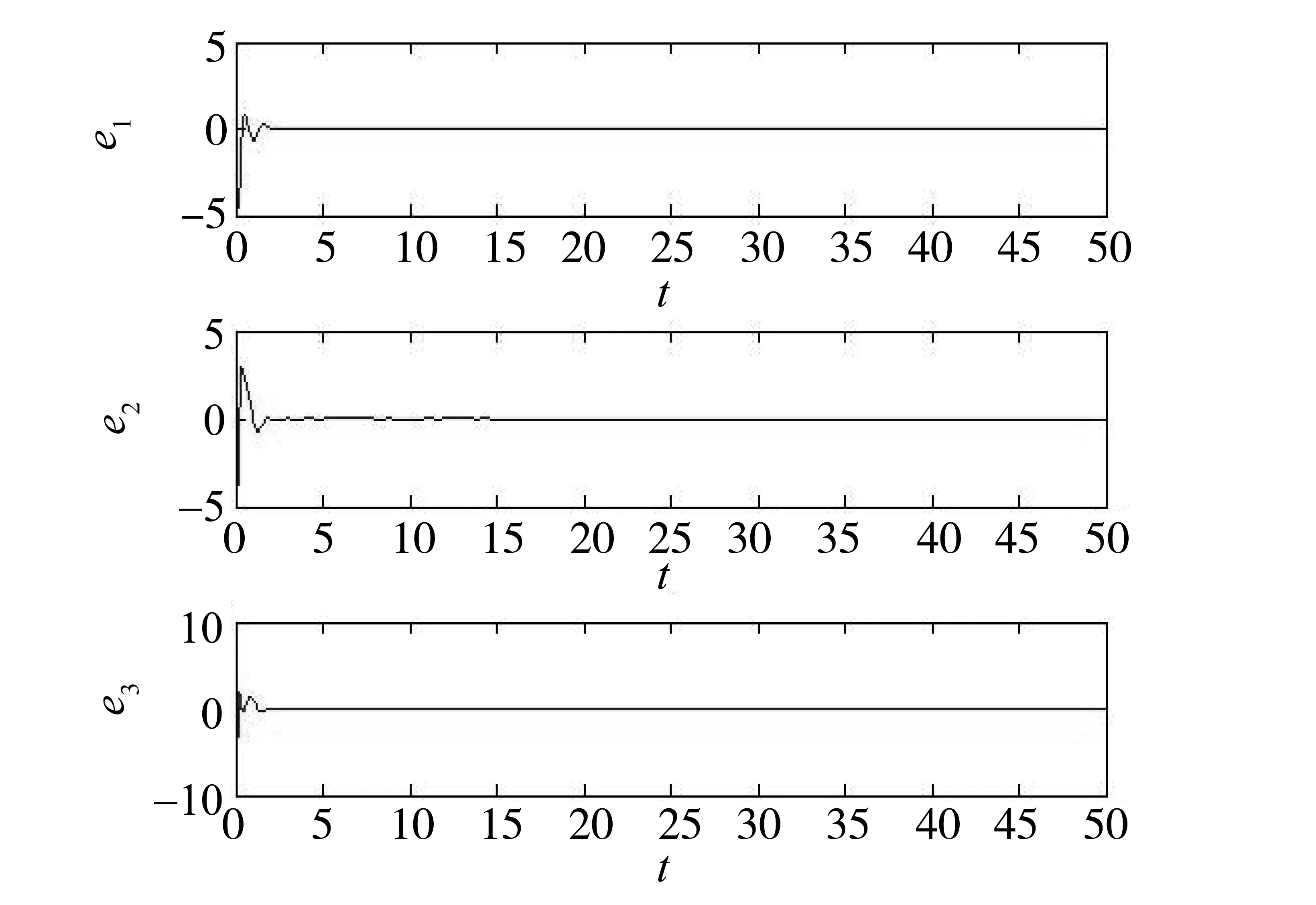
3 结 论

