全涂层的可穿透腔体散射问题的解的存在唯一性*
刘立汉
(重庆师范大学数学科学学院, 重庆401331)
全涂层的可穿透腔体散射问题的解的存在唯一性*
刘立汉
(重庆师范大学数学科学学院, 重庆401331)
利用变分法研究了全涂层的可穿透腔体散射问题的解的存在唯一性。首先,应用Green公式把微分方程转化为积分方程后,由Rellich引理和唯一延拓原理,证明了全涂层的可穿透腔体散射问题的解的唯一性。然后,由Dirichlet-to-Neumann算子理论、迹定理、连续嵌入定理和Lax-Milgram引理,证明了全涂层的可穿透腔体散射问题的解的存在性。
腔体; 散射;解的存在性;解的唯一性
声波和电磁波散射和反散射问题是近30年来应用数学中发展最迅速的领域之一,它是一个典型的非线性不适定问题,其研究成果被广泛应用于诸如几何物理学、雷达与声纳、地质勘探、生命科学、材料科学、遥感技术、模式识别、信号(图像)处理、无损探伤、医学诊断(CT)、工业控制及经济决策等自然科学和工程技术中。因此,对声波和电磁波散射和反散射问题数学理论与数值方法的研究,引起了国内外许多学者的兴趣和关注,也成为近年来一个非常活跃的研究热点,有关这方面的详细综述见专著[1-6]。
现有声波和电磁波散射和反散射问题的研究,大部分考虑的是经典的外部散射和反散射问题,即入射波在散射体的外部,而且测量数据(远场数据或近场数据)也在散射体的外部,详细的综述见专著[3]。然而,正如最近的文献[7-8]所述,在无损探测的许多实际工业问题中,点源(入射波)和测量数据(散射波)均在散射体的内部,由此产生了一类新型的研究课题:内部腔体散射和反散射问题。由于散射波被困在腔体内部,它会被腔体的边界反复反射,因此导致内部腔体散射和反散射问题比经典的外部散射和反散射问题物理上更加复杂。根据腔体的物理性质,内部腔体散射和反散射问题可分为如下两种类型:第一类是内部不可穿透腔体的散射和反散射问题,第二类是内部可穿透腔体的散射和反散射问题。
对于第一类模型,即内部不可穿透腔体的散射和反散射问题,根据腔体的物理性质,有3种基本边界条件:Dirichlet边界条件、Neumann边界条件和阻尼(impedance)边界条件。文献[8]于2012年首先证明了Dirichlet边界条件下内部不可穿透腔体散射和反散射问题的唯一性理论,并且利用线性采样法来反演腔体的位置及形状。继而,文献[9]又证明了阻尼边界条件下内部不可穿透腔体散射和反散射问题的唯一性理论,也利用线性采样法来反演腔体的位置、形状及其物理性质(阻尼函数)。随后,文献[10]证明了混合边界条件下内部不可穿透腔体散射和反散射问题的唯一性理论,同样利用线性采样法来反演腔体的位置、形状及其物理性质(阻尼函数)。文献[11]则利用分解法来反演Dirichlet和阻尼边界下内部不可穿透腔体的位置、形状及其物理性质(阻尼函数)。无论是线性采样方法还是分解法,它们一个共同的前提条件就是要排除内部特征值。然而,一般而言,散射和反散射问题本身与内部特征值没有任何关系,因此,这些方法对波数的要求显得有些多余。尽管内部特征值是离散的,在特定的区间内至多有有限个,但是当波数靠近这些特征值时,数值反演效果会随之变差。于是,文献[12]通过在原先散射系统中人为引入一个带阻尼边界的障碍物,这样就成功地排除了内部特征值。
线性采样法和分解法的优势在于不需要先验知道腔体的物理性质及其尺寸大小,但不幸的是,这些方法需要多点源的测量数据。如何利用内部单一点源测量数据来反演不可穿透腔体的位置、形状及其物理性质?文献[13]在对腔体尺寸大小的限制下,证明了由内部单一点源测量数据可以唯一确定Dirichlet边界条件下不可穿透腔体的位置及形状。文献[14]利用分裂法(Decomposition Method)研究了同样的问题,他们将原问题拆分为两步,即首先利用测量数据构造散射场,然后根据边界条件,利用入射场和已构造的散射场寻找边界,其中第一步是线性不适定的,第二步是非线性适定的,这样将原问题的两大难点(非线性和不适定)分裂开来。文献[15]在对腔体尺寸大小的限制下,证明了由内部单一点源测量数据可以唯一确定阻尼边界条件下不可穿透腔体的位置、形状及其物理性质(阻尼函数)。
对于第二类模型,即内部可穿透腔体的散射和反散射问题,目前这类问题的研究还很少。文献[16]于2014年首先证明了在传输边界条件下,由内部多点源测量数据可以唯一确定可穿透腔体的位置及形状,并利用线性采样法进行数值反演;文献[17]利用分解法研究同样的问题。对于更一般的混合边界条件,文献[18]基于外部传输特征值问题的谱性质分析,证明了由内部多点源测量数据可以唯一确定可穿透腔体的位置、形状及其物理性质,并利用线性采样法的思路,分析点源的奇异性,由此构造适当的指示函数,依次反演腔体的位置、形状以及物理性质。本文我们将考虑传导边界下可穿透腔体的散射问题。
1 全涂层的可穿透腔体散射问题

在声波散射(d=2)或电磁波散射(d=3)时,D表示一个充满如空气等的腔体,并且设为波数为k的参考介质。设Φ(·,y)(y∈D)为入射点源,定义如下:
(1)
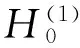
Δxu+k2u=δ(x-y),x∈D
(2)
而在腔体D内,总场w满足
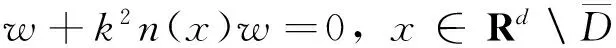
(3)
在边界∂D上,如下传导边界条件
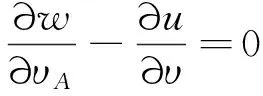
(4)
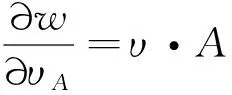
最后,还有Sommerfeld辐射条件,其给定如下:
(5)
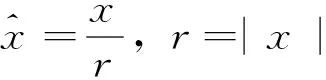
(6)
其中f和g由文献[21]可知
2 解的存在唯一性
在这一部分,我们将证明全涂层的可穿透腔体散射问题的解的存在唯一性。
2.1 解的唯一性


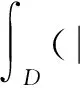
取上式两边的虚部,并且注意到Im (A)≤0,Im (n)≥0和η(x)≥η0>0,则有
即
由Sommerfeld辐射条件(5)可知
于是
从而

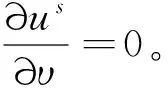
2.2 解的存在性
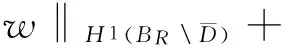
其中β是一个不依赖于Φ但依赖于R的正常数。
证明 在方程(2)和(3)左右两边同时乘以一个试验函数φ,并利用Green公式和传导边界条件(4)可知,定义在BR内的总场U满足
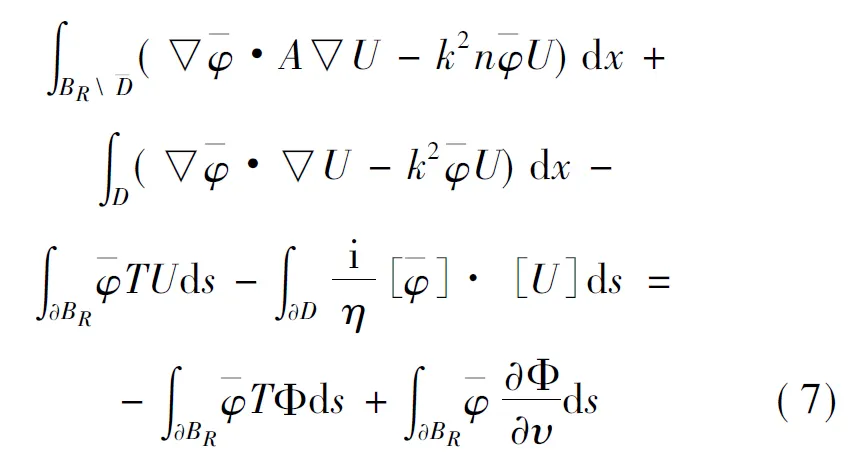
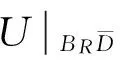
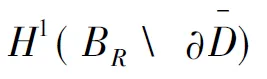
(4)

现在定义函数a1(U,φ)如下:
(5)
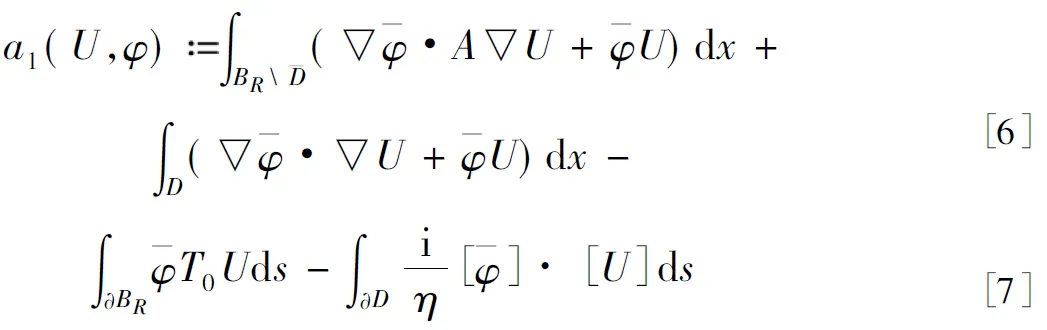
和定义函数a2(U,φ)如下:
(8)

(9)
其中T0是Dirichlet-to-Neumann算子T的负定部分,并且对于某一常数γ>0,有
‖

a1(U,φ)+a2(U,φ)=L(φ),
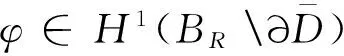
(8)
其中L(φ)为式(7)的右边,是一个有界的共轭线性泛函,即
最后,利用迹定理、Cauchy-Schwartz不等式、连续嵌入定理和对A,n,η的假设可知:我们很容易得到半线性形式a1(·,·)是有界的和严格强制的,半线性形式a2(·,·)是有界的。因此,利用Lax-Milgram引理和文献[1]的定理5.16可得解的存在性。
[1]CAKONIF,COLTOND.Aqualitativeapproachtoinversescatteringtheory[M].NewYork:Springer, 2014.
[2]CAKONIF,COLTOND,MONKP.Thelinearsamplingmethodininverseelectromagneticscattering[M].Philadelphia:CBMS-NSFRegionalConferenceSeriesinAppliedMathematics80,SIAM, 2011.
[3]COLTOND,KRESSR. Inverse acoustic and electromagnetic scattering theory [M]. 3rd ed. New York: Springer, 2013.
[4] KIRSCH A. An Introduction to the mathematical theory of inverse problems [M]. 2nd ed. New York: Springer, 2011.
[5] KIRSCH A, GRINBERG N. The factorization method for inverse problems [M]. Oxford: Oxford University Press, 2008.
[6] POTTHAST R. Point sources and multipoles in inverse scattering theory [M]. London: Chapman and Hall/CRC, 2001.
[7] JAKUBIK P, POTTHAST R. Testing the integrity of some cavity-the Cauchy problem and the range test [J]. Applied Numerical Mathematics, 2008, 58(6): 899-914.
[8] QIN H, COLTON D. The inverse scattering problem for cavities [J]. Applied Numerical Mathematics, 2012, 62(6): 699-708.
[9] QIN H, COLTON D. The inverse scattering problem for cavities with impedance boundary condition [J]. Advances in Computional Mathematics, 2012, 36(2): 157-174.
[10] HU Y, CAKONI F, LIU J. The inverse problem for a partially coated cavity with interior measurements [J]. Applicable Analysis, 2014, 93(5): 936-956.
[11] LIU X. The factorization method for cavities [J]. Inverse Problems, 2014, 30(1): 015006.
[12] QIN H, LIU X. The interior inverse scattering problem for cavities with an artificial obstacle [J]. Applied Numerical Mathematics, 2015, 88: 18-30.
[13] QIN H, CAKONI F. Nonlinear integral equations for shape reconstruction in the inverse interior scattering problem [J]. Inverse Problems, 2011, 27(3): 035005.
[14] ZENG F, SUAREZ P, SUN J. A decomposition method for an interior inverse scattering problem [J]. Inverse Problems and Imaging, 2013, 7(1): 291-303.
[15] QIN H, LIU J. Reconstruction for cavities with impedance boundary condition [J]. Journal of Integral Equations and Applications, 2013, 25(3): 431-454.
[16] CAKONI F, COLTON D, MENG S. The inverse scattering problem for a penetrable cavity with internal measurements [J]. AMS Contemporary Mathematics, 2014, 615: 71-88.
[17] MENG S, HADDAR H, CAKONI F. The factorization method for a cavity in an inhomogeneous medium [J]. Inverse Problems, 2014, 30(4): 045008.
[18] LIU L. The inverse scattering problem for a partially coated penetrable cavity with internal measurements [J]. Applicable Analysis, 2016: 1-25.
[19] ANGELL T, KIRSCH A. The conductive boundary condition for Maxwell’s equations [J]. SIAM J Appl Math, 1992, 52:1597-1610.
[20] ANGELL T, KIRSCH A. Optimization methods in electromagnetic radiation [M]. New York: Springer, 2004.
[21] MCLEAN W. Strongly elliptic systems and boundary integral equations [M]. Cambridge: Cambridge Uninversity Press, 2000.
The uniqueness and existence of solutions for the scattering problem for a fully coated penetrable cavity
LIULihan
(School of Mathematial Sciences, Chongqing Normal University, Chongqing 401331, China)
The uniqueness and existence of solutions for the scattering problem for a fully coated penetrable cavity are studied by using variational method. First, the differential equations are transformed into an integral equation by using the Green’s first identity. Then from the Rellich’s lemma and a unique continuation principle, the uniqueness of solutions for the scattering problem for a fully coated penetrable cavity is proven. Next, from the Dirichlet-to-Neumann operator, the trace theorem, the continuous embedding theorem and the Lax-Milgram’s lemma, the existence of solutions for the scattering problem for a fully coated penetrable cavity is also proven.
cavity; scattering; existence of solutions; uniqueness of solutions
2016-08-11 基金项目:国家自然科学基金数学天元青年基金(11426052);重庆市教育委员会科学技术研究项目(KJ1400522,KJ1600329);2013年重庆高校创新团队建设计划项目(KJTD201308)
刘立汉(1987年生),男;研究方向:数学物理方程的反问题;E-mail:mathsedu2013@163.com
O
A
0529-6579(2017)02-0036-04

