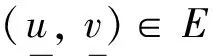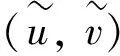伪抛物方程组解的全局存在
姜迪彪, 曾有栋, 魏 丹
(福州大学数学与计算机科学学院,福建 福州 350116)
伪抛物方程组解的全局存在
姜迪彪, 曾有栋, 魏 丹
(福州大学数学与计算机科学学院,福建 福州 350116)
研究如下非线性伪抛物方程组柯西问题解的全局存在性,ut-Δut=Δu+uαvp,vt-Δvt=Δv+uqvβ, 这里p,q≥0,α,β≥0. 首先应用压缩映射原理得到解的局部存在性, 之后运用上下解方法研究α,β≤1,pq≤(1-α)(1-β)时解的全局存在性.
非线性伪抛物方程组; 局部存在; 全局存在; 柯西问题
0 引言
考虑下面非线性伪抛物系统的柯西问题解的全局存在性, 有
式(1)中α,β,p,q≥0,并且满足α+p>0和β+q>0.u0(x)和v0(x)都是非负有界和适当光滑的函数. 这类方程描述了一类重要的物理过程,比如, 非线性扩散长波的单向传播, 透过裂缝岩石均匀流体的渗透, 传导问题中的双温控制模型.
对于伪抛物方程

当p≥1,q≥1,pq>1时确定了它的Fujita临界指标和第二临界指标分别是:

根据以往的研究, 式(1)爆破和全局存在临界指标以及解的渐进性质仍然是一个开放性的问题. 本研究对这些开放性问题进行初步探索, 得到式(1)解的局部存在性和在一定条件下解的全局存在性.
1 预备知识
对于非线性伪抛物系统(1), 类似于文献[3],可得
其中: I(t)=exp(-t(kΔ-I)-1Δ),B=-(kΔ-I)-1, 算子I(t)和B的性质参考文献[2-7].
定义1 如果(u,v)∈C([0,T];C(n)∩L∞(n))2且满足积分方程(4)和(5), 则称(u,v)是柯西问题(式(1))在[0,T]上的适度解.
引理1 设ε∈(0, 1), 式(1)的初值满足u0,v0∈C2+ε(n), 则式(1)在C([0,T];C(n)∩L∞(n))2中具有积分方程(4)、 (5)形式的适度解(u,v),该解属于(C1([0,T];C2(n)))2且是古典解.
证明 设(u,v)在C([0,T];C(n)∩L∞(n))2中是式(1)的适度解. 由算子I(t)和B的性质可得u,v∈C([0,T];Cε(n)), 对某个0<θ≤ε, 有uα,uq,vp,vβ∈C([0,T];Cθ(n)). 则可得u,v∈C([0,T];C2+θ(n)). 易证(u,v)满足式(1)且正是式(1)的古典解.
根据文献[2]可知对于非负初值, 柯西问题(式(1))的解也是非负的.
类似文[1]中定义2.2的叙述, 下面给出耦合适度上下解的定义.
定义2 称函数(u′,v′)是柯西问题在[0,T]上的上(下)适度解, 如果(u′,v′)∈C([0,T];C(n)∩L∞(n))2且满足
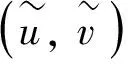
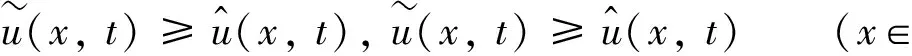
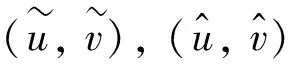
2 局部存在和全局存在
2.1 解的局部存在性
定理1 (局部存在性)设0≤u0, v0∈C(n)∩L∞(n),α, β≥0, pq>0,则存在T(0 证明 I)首先设p,q,α,β≥1,由标准的不动点定理即可推出式(4)和式(5)在n×[0,T], 0 设(u,v)∈X∩BR, 首先可得Φ1(u,v)≥0,Φ2(u,v)≥0. 又因为 其中:C1是大于零常数, 不依赖于T、u和u0. 因此, 如果令 则可得: 综上可得Ψ(u, v)∈X∩BR. 对于(u1, v1)∈X∩BR,(u2, v2)∈X∩BR, 可得 综上可知, 当R满足上面条件时,Ψ是XR上的压缩映射, 因此由Banach空间压缩映射原理可得结论. II)如果至少有一指标小于1, 存在性可采取文献[8]中相关性讨论得到. 为了简洁, 在这里简略说明如何证明0≤α<1,p,q,β≥1的情形, 一般的情形也可类似得到. 令序列{gn}是全局Lipschitz函数, 并且对任意给定的n满足: 考虑下面的逼近问题 像步骤I)部分一样讨论, 则在某个(0,T)×n上可得与方程组(6)相关的积分方程唯一非负适度解(un(t),vn(t)). 此外, 如果n≥m, 有un(t)≤um(t),vn(t)≤vm(t)成立. 因此, 序列{un(t)}和{vn(t)}非增且下方有界. 令n→∞, 也可得到与I)部分相关的结论. 证明完毕. 2.2 解的全局存在理论 定理2 设α≤1,β≤1和pq≤(1-α)(1-β), 初值满足0≤u0,v0∈Cα(n),α∈(0, 1)则对任意给定的T>0, 柯西问题(式(1))至少存在一个非负适度解. 另外记映射: Φi:C([0,T];C(n)∩L∞(n))→C([0,T];C(n)∩L∞(n)) (i=1, 2) 则 所以u,v∈C([0,T];C(n)∩L∞(n)). 此外 同理, 由qm≤l(1-β)和1/2 [1] CAO Y, YIN J X, WANG C P. Cauchy problems of semilinear pseudo-parabolic equation[J]. Journal of Differential Equations, 2009, 246(12): 4 568-4 590. [2] KAIKINA E I, NAUMKIN P I, SHISHMAREV I A. The Cauchy problem for a Sobolev type equation with a power nonlinearity[J]. Izv Ross Akad Nauk Ser Mat, 2005(1): 61-114. [3] YANG J G, CAO Y, ZHENG S N. Fujita phenomena in nonlinear pseudo-parabolic system[J]. Science China Mathematics, 2014, 57(3): 555-568. [4] GOPALA R V R, TING T W. Solutions of pseudo-heat equations in the whole space[J]. Archive for Rational Mechanics and Analysis, 1972, 49(1): 57-78. [5] KARCH G. Asymptotic behaviour of solutions to some pesudoparabolic equations[J]. Applied Mathematics Letters, 2012, 25(2): 111-114. [6] KARCH G. Large-time behaviour of solutions to nonlinear wave equations: higher-order asymptotics[J]. Mathematical Methods in the Applied Sciences , 1999, 22(18): 1 671-1 697. [7] SHOWALTER R E, TING T W. Pseudoparabolic partial differential equations[J]. Siam Journal on Mathematical Analysis, 1968, 88(1): 1-26. [8] AGUIRRE J, ESCOBEDO M. A cauchy problem forut-Δu=up: asymptotic behaviour of solution[J]. Annales De La Faculté Des Sciences De Toulouse, 1986, 8(2): 175-203. (责任编辑: 林晓) Global existence of solution to pseudo-parabolic system JIANG Dibiao, ZENG Youdong, WEI Dan (College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116, China) This paper deals with the Cauchy problem to nonlinear pseudo-parabolic systemut-Δut=Δu+uαvp,vt-Δvt=Δv+uqvβwhere,q≥0,α,β≥0. we first applied contraction mapping to obtain that local solutions are existence. And then we investigate that the solutions are global whileα,β≤1andpq≤(1-α)(1-β) by use upper and lower solutions method. nonlinear pseudo-parabolic system; local existence; global existence; Cauchy problem 10.7631/issn.1000-2243.2017.03.0312 1000-2243(2017)03-0312-05 2015-04-17 曾有栋(1961-), 教授, 主要从事偏微分方程研究, zengyd@fzu.edu.cn 国家自然科学基金资助项目(2016J06001) O175.26 A