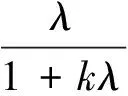一类带非线性记忆的伪抛物方程解的爆破

魏 丹, 曾有栋, 姜迪彪

(福州大学数学与计算机科学学院, 福建 福州 350116)



一类带非线性记忆的伪抛物方程解的爆破

魏 丹, 曾有栋, 姜迪彪

(福州大学数学与计算机科学学院, 福建 福州 350116)

研究一类带非线性记忆的伪抛物方程解的爆破性质. 先用严格压缩映射及不动点定理证明解的局部存在唯一性, 并通过特征函数法结合微分不等式组新性质的一个变体法证明其解在一定条件下爆破.

伪抛物方程； 非线性记忆； 爆破

0 引言

本文研究以下带非线性记忆的伪抛物方程的初值问题：

其中：p≥1,κ≥1,μ(x)∈Cγ(Rn),γ>0,μ(x)是Rn上非负有界的非平凡函数；u0(x)是Rn上非负非平凡的有界充分光滑的函数.

近年来，对于伪抛物方程的研究较为广泛，它可以反映许多重要的物理现象，如穿过有裂缝岩石的均匀流体的渗流[1]，传导问题中双温控制模型[2]，人口动力学理论[3]，二阶非平稳流模型[4]，刻画一类非线性色散长波的单向传播[5]等. 目前，对伪抛物方程的研究已取得较大的进展，如文献[6]研究如下伪抛物方程解的渐进行为.

ut-ηΔut-vΔu=f(x,u,u)

(2)

文献[7]研究如下半线性伪抛物方程解的Fujita临界指标.

对于伪抛物方程的第二临界指标问题也有了相应的成果. 杨春晓等[8]讨论Cauchy问题(3)的第二临界指标和生命跨度.

在单个伪抛物方程基础上，杨金戈等[9]研究如下伪抛物方程组:

其中：p,q≥1,pq>1,α>0,u0(x),v0(x)非负有界且适当光滑，讨论式(4)的临界Fujita指标、 第二临界指标和解的全局性质.

目前，对于伪抛物方程的非局部问题的研究非常少，本文根据上述文献以及文献[10-11]的内容，研究带有非线性记忆项的伪抛物方程解的爆破性质.

特别地，当κ=1时，本文将给出p=1时的全局无界上解.

1 局部解的存在性

本节考虑Cauchy问题(1)的适度解, 当初值充分光滑时此适度解正是(1)的古典解. 下文将证明这样的解的存在性和唯一性, 并建立比较原理.

正如文献[12-13], Cauchy问题(1)在[0,T],T>0的一个古典解满足以下积分方程

其中:

定义1 积分方程(6)的一个解u∈C([0,T];C(Rn)∩L∞(Rn))称为Cauchy问题(1)在[0,T]的一个适度解.

固定T>0,α∈(0, 1), 1≤q2≤q1≤∞,m∈N, 且1≤q≤∞. 对于算子B和g(t), 以下不等式在文献[12-16]已证.

下文将证明当初值充分光滑时, Cauchy问题(1)的适度解就是古典解.

定理1 设α∈(0, 1)，对Cauchy问题(1)带初值u0∈C2+α(Rn), 在C([0,T];Cb(Rn))中具有积分方程(6)形式的适度解u属于C1([0,T];C2(Rn))且就是古典解. 其中Cb(Rn)表示Rn上的有界连续函数.

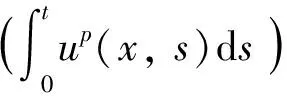
由式(8)和(13)有:

这表明u∈C1([0,T];C2+β(Rn))⊂C1([0,T];C2(Rn)). 易证u满足(1)且正是(1)的古典解.

由文献[13]知积分方程(6)可写成以下核函数的积分形式

其中:

下文将证明以下形式的极值原理.

引理1(Cauchy问题的极值原理) 令u是以下Cauchy问题的一个解.

其中：a(x,t),b(x,t),c(x,t)是QT上非负有界连续函数. 则对∀(x,t)∈QT, 有u(x,t)≥0.

证明 令u0(x)是初值,m(x,t)是加在式(15)右边的补偿函数使之成为一个方程. 由核函数的表达式，u(x,t)可以表示成

令

由于u0(x)和m(x, t)及核函数都是非负的, 所以h0(t)也是非负的.

定义算子E把C[0, T]映到C[0, T]:

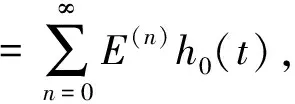
因为H(x-y, t-τ)≥0并且a(x, t), b(x, t), c(x, t)≥0, 则由数学归纳法有E(n)h0(t)≥0，所以u(x, t)≥0，其中t在一个很小的区间里. 最后, 重复以上过程就可以得到u(x, t)≥0在整个区间[0, T]上都成立.

接下来证明局部可解性.

定理2 设α∈(0, 1), u0(x)∈C2+α(Rn)是非负有界非平凡函数, 如果p≥1, κ≥1, μ(x)∈Cγ(Rn), γ>0, μ(x)是非负有界非平凡函数，则存在T>0，使得问题(1)存在唯一非负古典解.

设u∈Xδ，由式(14)知φ(u)是非负的. 则由式(7)、 (9)有

则有φ(u)∈Xδ. 类似地, 对∀u1,u2∈Xδ, 由式(7)和(9)得，

又因为

若取

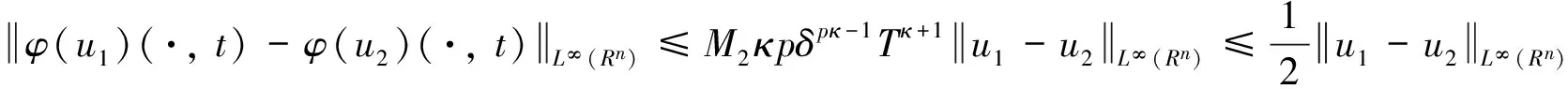
由以上讨论可知若δ满足式(18)且T满足式(19)、 (20)，则φ是Xδ上的严格压缩映射. 所以问题(1)有唯一适度解0≤u∈C([0, T]; Cb(Rn)). 由定理1知问题(1)在[0, T]中有唯一古典解.

2 解在有限时间内爆破

定理3 假设κ=1, p>1或κ>1, p≥1，设0≤u∈C1([0, T); C2(Rn))，是问题(1)的解，u0(x)是Rn上非负非平凡的有界充分光滑函数，μ(x)∈Cγ(Rn), γ>0, μ(x)是非负有界非平凡函数，则T<∞.

由定理条件知，对任意t∈(0, T)，有u(x, t)≥0且u0(x)是Rn上非负非平凡函数. 则对x∈Rn，有z(t)>0, 0

相应的结果可由以下的引理得到.

引理2 设p>1, 且κ≥1，设y, z∈C1(0, T)，且在(0, T)上有y≥0, z>0，使得

则T<∞.

所以

接下来考虑两种情况.

情况1s=1,κ>1选取zκ(0)>ε，令m=min(κ,p)>1. 由z是增函数，有

(2Cε+3)[z+y]′≥zκ+yp+y≥[z(0)]κ-mzm+ym, 0≤t

利用不等式

可得[z+y]′≥C[z+y]m, 0≤t0，因此T<∞.

C″ε[zθ+y]′≥zκ+yps+y≥[z(0)]κ-θmzθm+ym(0≤t

由式(23)，得[zθ+y]′≥C[zθ+y]m, 0≤t0，从而T<∞，引理证毕.

定理4 (比较原理)令f, g:[0, ∞)→[0, ∞)是[0, ∞)上非负非递减的可导函数. 假设u, v∈C1([0, T]; C2(Rn))且u≥δ>0, v≥0，满足

u(x, 0)≥v(x, 0) (x∈Rn)

则对任意x∈Rn, 0

证明 令a(x,t),b(x,t),c(x,t)是如下定义的连续函数：

b(x, t)=g(v), 因为u≥δ>0, a(x, t), b(x, t), c(x, t)是非负有界的，由引理1即证.

考虑问题(5)，其中p≥1，函数μ(x)在Rn上Hölder连续，μ(x)是非负有界非平凡函数，u0(x)为非负有界光滑函数.

定理5 设u0∈C2+α(Rn),u0≥0,u0≢0, 设u≥0为问题(5)的解，则

1) 如果p>1，则问题(5)的解u依L∞范数在有限时间内爆破.

2) 如果p=1，则问题(5)有全局无界上解.

证明 1) 这是定理3的特殊情况，显然成立.

[1] BARENBLAT G, ZHELTOV I, KOCHIVA I. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks[J]. Appl Math Mech, 1960, 24(5): 1 286-1 303.

[2] CHEN P J, GURTI M E. On a theory of heat conduction involving two temperatures[J]. Zeitschrift Fur Angewandte Mathematics and Physik, 1968, 19(4): 614-627.

[3] PADRON V. Sobolev regularization of some nonlinear ill-posed problems[D]. Minneapolis:University of Minnesota, 1990.

[4] TING T W. Certain non-steady flows of scend-order fluids[J]. Archive for Rational Mechanics and Analysis, 1963, 14(1): 1-26.

[5] BENJAMIN T B, BONA J L, MAHONY J J. Model equations for long waves in non-linear dispersive systems[J]. Philosophical Transactions of the Royal Society A, 1972, 272(1 220): 47-78.

[6] LIU Y, JIANG W, HUANG F. Asymptotic behavior of solution to some pseudo-parabolic equation[J]. Applied Mathematics Letters, 2012, 25(3): 111-114.

[7] CAO Y, YIN J X, WANG C P. Cauchy problems of semilinear pseudo-parabolic equations[J]. Differential Equations, 2009, 246(12): 4 568-4 590.

[8] YANG C X, YIN J X, ZHENG S N. Second critical exponent and life span for pseudo-parabolic[J]. Differential Equations, 2012 , 253(12): 3 286-3 303.

[9] YANG J G, CAO Y, ZHENG S N. Fujita phenomena in nonlinear pseudo-parabolic system[J]. Science China Mathematics, 2014, 57(3), 555-568.

[10] SOUPLET P. Blow-up in nonlocal reaction-diffusion equations[J]. SIAM Journal on Mathematical Analysis, 1998, 29(6): 1 301-1 334.

[11] LI Y X, XIE C H. Blow up for semilinear parabolic equations with nonlinear memory[J]. Zeitschrift fur Angewandte Mathematik und Physik, 2004, 55 (1): 15-27

[12] GOPALA Rao V R, TING T W. Solutions of psedo-heat equations in the whole space[J]. Archive for Rational Mechanics and Analysis, 1972, 49(1): 59-78

[13] KAIKINA E I, NAUMKIN P I, SHISHMAREV I A. The Cauchy problem for a Sobolev type equation with power like nonlinearity[J]. Izv Math, 2005, 69(1) : 59-111.

[14] KARCH G. Large-time behavior of solutions to nonlinear wave equations: higher-order asymptotics[J]. Math Methods Appl Sci, 1999, 22(18) : 1 671-1 697

[15] CHEN P J, GURTIN M E. On a theory of heat conduction involving two temperatures[J]. Zeitschrift fur Angewandte Mathematik und Physik，1968, 19(4): 614-627.

[16] TING T W. Parabolic and pseudo-parabolic partial differential equations[J]. Math Soc Japan, 1969, 21(3)： 440-453

[17] SOUPLET P. Nonexistence of global solutions to some differential inequalities of the second order and applications[J]. Portugaliae Mathematica, 1995, 52(3): 289-300.

(责任编辑： 蒋培玉)

Blowup property of solutions to pseudo-parabolic equation with nonlinear memory term

WEI Dan, ZENG Youdong, JIANG Dibiao

(College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116, China)

We investigate the blowup property of solutions to the pseudo-parabolic equation. By using constructing mapping and the fixed point theory，we obtain the existence and uniqueness of local solutions. Then we obtain that the solutions blow up relying on a variant of the eigenfunction method combined with new properties on systems of differential inequalities.

pseudo-parabolic equation; nonlinear memory term； blowup

10.7631/issn.1000-2243.2017.03.0317

1000-2243(2017)03-0317-06

2015-04-22

曾有栋(1961-)，教授，主要从事偏微分方程的研究，zengyd@fzu.edu.cn

国家自然科学基金资助项目 (71273053)； 福建省自然科学基金资助项目(2014J01009)

O175.26

A