一种三维实空间上框架构造的算法及其实现

罗智鹏，朱玉灿

(福州大学数学与计算机科学学院，福建 福州 350116)



一种三维实空间上框架构造的算法及其实现

罗智鹏，朱玉灿

(福州大学数学与计算机科学学院，福建 福州 350116)

根据有限维框架构造理论，在给定框架算子特征值及其模长序列条件下，提出一种三维实空间上具体构造框架的算法，并以算例验证了该算法的准确性和灵活性.

框架构造算法； 三维实空间； 框架算子

0 引言

为合成算子，其对偶算子

T*:Hn→Cm,T*f=(〈f,f1〉, 〈f,f2〉, …, 〈f,fm〉)T

为分析算子. 令S=TT*, 即

命题1[8]下列两个叙述等价.

2) 矩阵F的秩为n.

如果Λ为对角矩阵且diag(Λ)=(λ1,λ2, …,λm)，则存在m阶正交矩阵O，使得

1 算法设计

1.1 算法思想

R3中矩阵S是3阶正定矩阵，存在正交矩阵O和对角矩阵Λ，使S=OΛO*成立，其中diag(Λ)=(λ1,λ2,λ3)，λi(i=1, 2, 3)为S的特征值(设λ1≥λ2≥λ3>0). 取m×3阶矩阵Δ如下：

则ΔΔ*为m阶对角矩阵，且diag(ΔΔ*)=(λ1,λ2,λ3, 0, …, 0)，这里m为框架元素个数. 由命题2知，当满足条件：

∀

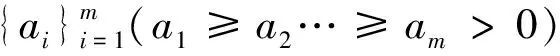
1.2 三阶正交矩阵O的构造

由前面分析知矩阵S是一个三阶正定矩阵，故存在三阶正交矩阵O和对角矩阵Λ使S=OΛO*. 反之，已知对角矩阵Λ，即已知三个正实数λ1、λ2、λ3时，取不同的矩阵O将对应着不同的矩阵S. 此时矩阵S只由正交矩阵O决定. 本研究以下面方式构造三阶正交矩阵[9]O：

其中:a、b、c由控制参数θ、φ确定，它们的关系如下：

a=sinφcosθ，b=sinφsinθ，c=cosφ

因此，正交矩阵O由控制参数θ、φ、γ决定. 取值范围分别为：θ∈[0, 2π],φ∈[0, π],γ∈[0, 2π]. 从而不同的控制参数可以得到不同的矩阵O，生成不同的框架算子S. 特别地，当需求为生成紧框架时，可令θ=0，φ=π/2，γ=0，即O=E3，其中E3为三阶单位矩阵.

对于Oj的构造，令l=m-j+1. 设Aj为l阶对角矩阵，它在Oj-1的构造过程中迭代生成，其中初始矩阵A1为m阶对角矩阵，且

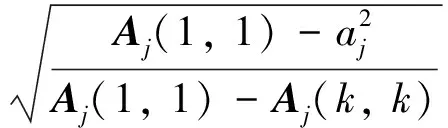
最后构造如下形式的l阶正交矩阵Oj：

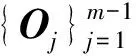
1.4 算法描述

输出： 矩阵F.

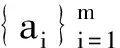
第二步： 判断框架类型控制参数Y. 若Y=0，则以式(3)构造正交矩阵O; 若Y=1，则O=E3，进入第三步.

第三步： 初始化控制变量j=1，如式(4)所示构造对角矩阵A1，进入第四步.

第四步： 初始化控制变量i=2，进入第五步.

第六步： 以式(5)方式构造正交矩阵Oj， 进入第七步.

第七步： 若j=m-1，进入第八步； 否则生成对角矩阵Aj+1，令j=j+1，返回第四步.

第八步： 初始化控制变量w=1. 如果m=3，进入(二)； 否则进入(一).

(一)构造w+2阶矩阵Bw+2：

令Om-1-w=Bw+2Om-1-w. 判断等式w=m-2是否成立，如果成立，进入(二)； 否则令w=w+1，返回(一).

1.5 算法实现的伪代码

根据上述算法描述给出对应的伪代码，如表1所示.

表1 伪代码

1.6 算例及验证分析

表2 参数θ、 φ、 γ取不同值时的输出结果

表3 参数θ、φ、γ取不同值时输出的矩阵F的秩、FF*以及OΛO*比较

Yθφγrank(F)FF∗OΛO∗013534．35781．37180．41721．37188．56770．30770．41720．30772．0745éëêêêùûúúú4．35781．37180．41721．37188．56770．30770．41720．30772．0745éëêêêùûúúú03153 6．6674-2．9562-0．3842-2．9526 4．6008 1．3562-0．3842 1．3562 3．7318éëêêêùûúúú 6．6674-2．9562-0．3842-2．9526 4．6008 1．3562-0．38421．3562 3．7318éëêêêùûúúú05313 5．4287-2．2529 0．5205-2．2529 7．4891-0．4549 0．5205-0．4549 2．0822éëêêêùûúúú 5．4287-2．2529 0．5205-2．2529 7．4891-0．4549 0．5205-0．4549 2．0822éëêêêùûúúú03333 8．3866 0．7016-1．8296 0．7016 4．1047-0．1604-1．8296-0．1604 2．5265éëêêêùûúúú 8．3866 0．7016-1．8296 0．7016 4．1047-0．1604-1．8296-0．1604 2．5265éëêêêùûúúú

表4 参数θ、 φ、 γ取不同值时输出结果的模长

表5给出了在框架类型参数Y取1时所得到的框架，易验证所得到框架即为紧框架. 在本例中，若λ1=λ2=λ3=5，同时取Y=1，O=E3，则根据算法编写相应程序，运行结果见表5 (精度取四位小数).

表5 参数Y=1时的输出结果

此时可验证FF*=S=OΛO*为对角矩阵，且diag(S)=(5, 5, 5).

2 结论

以框架存在性定理为理论依据，在模长序列和框架算子特征值序列给定的条件下设计框架构造算法，解决了三维空间中具体构造框架的问题，并以算例验证了算法的准确性和灵活性. 后续我们将尝试把该算法推广到高维空间上，使其能更广泛地应用于高维空间的数据处理. 同时也将尝试对算法进行优化，使之执行速度更快.

[1]HEATHRW,PAULRAJAJ.LineardispersioncodesforMIMOsystemsbasedonframetheory[J].IEEETransactionsonSignalProcessing, 2002, 50(10): 2 429-2 441.

[2]CANDESEJ,DONOHODL.NewtightframesofcurveletsandoptimalrepresentationsofobjectswithpiecewiseC2singularities[J].CommunicationsonPureandAppliedMathematics, 2004, 57(2): 219-266.

[3]CHANRH,RIEMENSCHNEIDERSD,SHENLX, et al.Tightframe:anefficientwayforhigh-resolutionimagereconstruction[J].AppliedandComputationalHarmonicAnalysis, 2004, 17(1): 91-115.

[4]ANTEZANAJ,MASSEYP,RUIZM, et al.TheSchur-Horntheoremforoperatorsandframeswithprescribednormsandframeoperator[J].IllinoisJournalofMathematics, 2007, 51(2): 537-560.

[5]CAHILLJ,FICKUSM,MIXONDG, et al.Constructingfiniteframesofagivenspectrumandsetoflengths[J].AppliedandComputationalHarmonicAnalysis, 2011, 35(1): 52-73.

[6]CASAZZAPG,LEONMT.Existenceandconstructionoffiniteframeswithagivenframeoperator[J].ItalianJournalofPureandAppliedMathematics, 2010, 63(2): 149-157.

[7] 王维, 朱玉灿. 一种二维实空间上构造框架的算法及其实现[J]. 福州大学学报(自然科学版)， 2016, 44(3):348-353.

[8]CASAZZAPG,KUTYNIOKG.Finiteframes:theoryandapplications[M].Boston:BirkhäuserBasel, 2012.

[9] 黄慕欢, 林茜. 正交矩阵在空间坐标变换中的作用[J]. 数学学习, 2009, 12(2):24-26.

(责任编辑： 林晓)

An algorithm for constructing frames for the three-dimensional real space and its implementation

LUO Zhipeng, ZHU Yucan

(College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116, China)

We present an algorithm for constructing frames on the three-dimensional real space under given the eigenvalues of the frame operator and predetermined lengths of frame’s vectors. Example is used to verify the accuracy and flexibility of the algorithm.

algorithm of constructing frame; three-dimensional real space; frame operator

2015-05-22

朱玉灿(1963-)，教授，主要从事框架理论、 几何函数论、 多复变函数几何理论研究，zhuyucan@fzu.edu.cn

福建省自然科学基金资助项目(2014J01007) ; 福建省教育厅A类资助项目(JA14041)； 福州大学科技发展基金资助项目(2012-XQ-29)

10.7631/issn.1000-2243.2017.03.0301

1000-2243(2017)03-0301-06

O177.1

A