有限差分-谱方法求解Allen-Cahn方程的误差分析

李娴娟

(福州大学数学与计算机科学学院，福建 福州 350116)



有限差分-谱方法求解Allen-Cahn方程的误差分析

李娴娟

(福州大学数学与计算机科学学院，福建 福州 350116)

Allen-Cahn方程； 有限差分； 谱方法； 误差分析

0 引言

考虑Allen-Cahn方程：

其中:Ω⊂d,d=2, 3为有界区域;u表示合金的密度;ε表示交面厚度;n为外法向;f(u)=f′(u)，F(u)为能量势. 齐次Neumann边界条件说明合金在边界墙外没有质量损失. Allen-Cahn方程可视为Liapunov能量泛函E(u)在L2中的梯度流.

(f(a)-f(b), a-b)≥γ1(f ′(a)(a-b), a-b)-

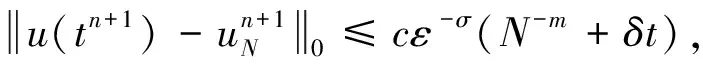
1 重要的引理

(ΠNu-u,vN)=0 (∀vN∈PN)

(

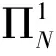
引理1 设Allen-Cahn算子LAC:=-Δ+f′(u)I的特征值满足：

有特征值估计

根据式(7)、 (10)、 (12)以及式(14)得：

综合式(11)以及式(15)可得特征值估计式(13)成立.

2 一阶有限差分-谱方法全离散格式

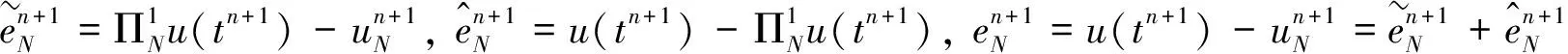
则

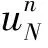
其中:δt以及N满足

证明 将方程(1)两端同时乘以vN并在Ω上积分得：

(ut,vN)+(u,

对方程(20)取t=tn+1，并与方程(16)相减得：

接下来逐项估计式(22).

由Cauchy-Schwarz不等式以及Young不等式得:

由引理1以及假设(5)得：

将式(23)～(27)代入方程(22)得：

对方程(28)两端同时求和并利用不等式(8)～(9), 文献[6]中性质2以及式(47)得：

注意到(19a), 则有

最后根据归纳法证明结论, 假设:

根据方程(30)并应用Gronwall不等式得:

[1] ANDERSON D M, MCFADDEN G B, WHEELER A A. Diffuse-interface methods in fluid mechanics[J]. Annual Review of Fluid Mechanics, 1998, 30(1): 139-165.

[2] DU Q, LIU C, WANG X Q. Simulating the deformation of vesicle membranes under elastic bending energy in three dimensions[J]. Journal of Computational Physics, 2006, 212(2): 757-777.

[3] LIU C, SHEN J. A phase field model for the mixture of two incompressible fluids and its approximation by a Fourier-spectral method[J]. Physica D, 2003, 179(3/4): 211-228.

[4] SHEN J, YANG X F. Numerical approximations of Allen-Cahn and Cahn-Hilliard equations[J]. Discrete and Continuous Dynamical Systems, 2010, 28(4): 1 669-1 691.

[5] DU Q, NICOLAIDES R A. Numerical analysis of a continuum model of phase transition[J]. SIAM Journal on Numerical Analysis, 1991, 28(5): 1 310-1 322.

[6] FENG X B, PROHL A. Numerical analysis of the Allen-Cahn equation and approximation for mean curvature flows[J]. Numerische Mathematik, 2003, 94(1): 33-65.

[7] YE X D. The legendre collocation method for the Cahn-Hilliard equation[J]. Journal of Computational and Applied Mathematics, 2003, 150(1): 87-108.

[8] CANUTO C, HUSSAINI M Y, QUARTERONI A,etal. Spectral methods: fundamentals in single domains[M]. Berlin: Springer, 2006.

(责任编辑： 林晓)

Error analysis of finite difference -spectral method for Allen-Cahn equations

LI Xianjuan

(College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116，China)

We investigate the error analysis of finite difference/spectral method for Allen-Cahn equations, where a vary small parameterεrepresents the interfacial width. The error analysis shows that if the time stepδtis small enough and polynomial orderNis large enough, then the error bound of the fully discrete schemes depends on the termε-σwhen the regularity of initial datau0depends on the same termε-σ. This result improves the error bound in which depends on e

Allen-Cahn equation; finite difference method; spectral method; error analysis

10.7631/issn.1000-2243.2017.03.0307

1000-2243(2017)03-0307-05

2016-11-05

李娴娟(1982-)，副教授，主要从事偏微分方程数值解方面研究，xjli@fzu.edu.cn

福建省教育厅科技资助项目(JA14034)； 福建省自然科学基金资助项目(2016J01013)

O241.8; O241.1

A