以活动促内化 借变式求明晰

高巍+执教+张翼文

【教学内容】人教版三年级上册《周长》P83-84

【课前思考】

1.学生的数学经验有哪些？

学生在一、二年级已经认识了三角形、平行四边形、长方形、正方形等平面图形，并且已经掌握了这些平面图形的基本特征。学生在测量中对边线的一维特征已经有所认知，对二维的平面图形“封闭”“边线”“大小”等有了模糊经验。

2.学生的生活经验对此课的学习有何影响？

在日常的生活中，学生对周长也有一定的了解，如头围、胸围等。但是，学生在对于面的感知上，大小、颜色、形状带来的刺激更为强烈，很少有关注到边线的长短。虽然周长的学习在面积的认识之前，但是学生对于面的感知的直接经验对本节课的学习带来了负迁移。

3.在后续的学习中学生一般会遇到哪些困难？

在图形与几何领域，学生经常将周长与面积混淆。算面积时求了周长，算周长时却用面积公式。再有，在后续的学习中，暴露出学生对于不规则图形、组合图形的周长或半个图形的周长不够明确，认知出现困难。这当然与周长意义的概念不够清晰有关，同时也说明，图形的周长与面积是相互依存、不可割裂的。在周长的教学中需伴随对面积的辨析。

4.“周长”这一概念的本质意义到底是什么？

教材中给出的周长定义是“封闭图形一周的长度”。周长的本质就是长度。那么初步认识周长，自然离不开对其长度的测量和计算。测量活动是学生感悟周长实际含义的有效方式，也是探究周长计算方法的前提，更是符合该年段学生特点的有效学习方式。

【教学目标】

知识技能：建立周长的概念；能根据图形特征探究不同的周长测量方法；区别周长与大小，为面积学习打好思辨基础。

数学思考：借助学生已有经验和有效活动，引导学生经历、体验和感悟周长的本质意义，渗透“化曲为直”的思想，突出周长的一维属性。

问题解决：在概念建立的过程中，经历猜想、验证、比较、实践等数学活动，培养学生的动手能力、观察能力及空间想象能力。

情感态度：培养学生独立思考和合作交流的学习方法和积极的学习态度，激发学习数学的兴趣。

【教学过程】

一、指一指，描一描，初步感知周长的意义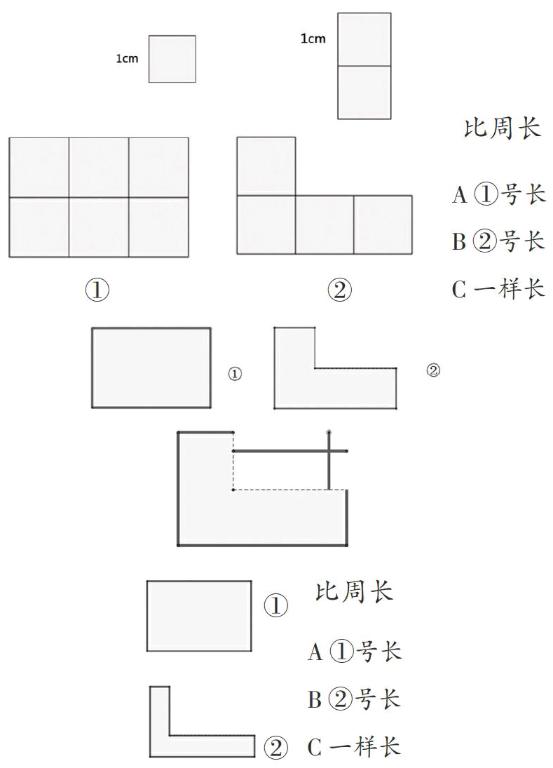

1.谈话引入，探寻知识起点。

师：同学们，今天我们来学习周长。（板书：周长）对于周长，你有哪些了解呢？

生：周長就是7天。

生：（指书的边缘）周长就是这里。

生：周长就是一圈。

师：高老师带来了几个图形，请你把自己心目中认为的周长在图形上描出来。比一比，看谁描得又快又美观？

2.初描周长，激活原有经验。

3.反馈比对，初步建立概念。

师：同学们都描出了自己心目中认为的图形的周长。谁愿意把刚才描的过程上来展示一下？生逐个描图形的边线。

师：刚才这位同学是从这里开始描的，现在老师从这里开始描可以吗？一起来描描看。

师：为了让同学看得更清楚些，高老师在电脑上将同学们刚才描的过程再展示一次，请你仔细观察：这些图形在描的时候有什么异同？

生：它们描的都是图形的边线。

生：前四个图形都是从哪里开始到哪里结束，描了整整一周。最后一个图形描的时候回不到起点。

生：最后一个图形有缺口，不封闭。

师：有缺口的图形，我们在描的时候就做不到再回到起点。这种没有缺口的图形数学上有一个名字叫封闭图形。数学上把封闭图形一周的长度叫作图形的周长。

师：刚才的这几个图形哪些有周长？哪些没有周长呢？

生：前四个图形有周长，最后一个图形没有周长，因为它没有封闭。

师：如果我们让这个图形变得也有周长，你能帮帮它吗？

【评析】开篇点题——周长，通过师生对话探寻学生的认知起点；通过描一描，初步建立周长的概念——图形边线的一周的长度；设置矛盾冲突，最后一个不封闭图形找不到周长，从而完善周长的概念——封闭图形一周的长度。此环节的设计，遵循学生的认知规律与经验起点，层层递进，逐步揭示周长的概念。最后学生通过对不封闭图形的改造，打破了他们原有的认为只有规则图形才有周长的思维定势，进一步明晰周长的本质属性。

二、量一量、算一算，凸显周长的一维属性

1.估一估，谁的周长最长？

师：（指四个描出周长的图形）请你估测一下，谁的周长最长呢？

生：正方形的周长最长，因为它最大。

生：树叶的周长最长，因为它的边凸凹不平，可能很长。

生：长方形的周长最长，因为它那么长。

师：同学们出现了不同的意见，我们来测量一下吧！

2.量一量，谁的周长最长？

同桌合作测量。

（1）选择信封中合适的工具测量图形的周长。

（2）将测量的结果写在相应图形的下面。

3.反馈。

师：你们测量的是哪个图形的周长？你是怎么量的？周长是多少？

生：我测量的是正方形的周长，我先用尺子量出了一条边的长度是10厘米，四条边的长度就是10乘4等于40厘米。

生：长方形的周长也可以用尺子去量，两条长边加上两条短边的总和是46厘米。

生：圆形的周长不能用直尺测量了，我們让圆在软尺上滚了一圈，结果量出来是43厘米。

生： 树叶的边线是曲线，而且凸凹不平，我们采用了用线绕的办法，将线绕在树叶的边缘上，再把线拉直，就可以用直尺测量长度了。

师：现在谜底终于揭晓了，刚才哪些同学猜对了？有什么想说的吗？

生：图形的周长和它所有边线的长度有关，和面的大小无关。

生：凸凹多一点的曲线拉直了可能会更长。

师：是的，刚才你们猜得那么准。就是因为你们有一双善于观察的眼睛，还有非常理性的思考。找准周长到底在哪里，再把它化曲为直，估计它的长度有多长。

【评析】教师设置“猜猜谁的周长最长”这一任务驱动，学生产生了测量的欲望。根据不同图形的特点，学生选择合适的测量工具与方法，在测量中进一步内化周长的概念——封闭图形一周的长度。特别值得一提的是，在学生测量后汇报各个图形周长时，教师随机将每个图形绕在边上的线展开拉直呈现。这种将二维与一维的巧妙过渡与呈现，对学生理解周长的一维属性来说，既直观而又深刻。

三、组一组、分一分，辨析周长的本质意义

1.拼一拼。

课件出示一个边长为1厘米的正方形，请生汇报周长。接下来再出示一个正方形，将两个正方形组合成一个新图形。

师：这个新图形的周长又会是多少呢？

生：一个正方形的周长是4厘米，两个正方形的周长就是4×2=8厘米。

生：应该是7厘米才对，因为中间有两条边重叠在一起了。

生：好像不对吧，两个正方形拼在一起，原来的边长没有都在周长里。

师：看来把两个图形拼在一起，周长并不是原来图形周长的简单叠加。我们要找到组合后图形的周长到底在哪里。

2.比一比。

课件出示①号图形和②号图形。比一比两个图形的周长，你同意哪个观点？

师：听起来意见不太统一哦！不急，可以和你的同桌一起商量一下。

反馈：

生：我们数了两个图形的周长都是10条边长组成的，所以一样长。

生：虽然它们一个是4个正方形拼成的，一个是6个正方形拼成的，但是里面的边是没用的，外面边线的长度是一样的。

师：同学们的办法都很好，借助格子图比较周长的长短，如果没有了这些格子，你们还能说明两个图形的周长一样长吗？

生：我们可以采用“移”的办法，将几条边组合起来进行比较。（伴随学生的指示，师白板呈现）

【评析】对于三年级的学生来说，一一对应、直观形象是他们的认知特点。比较两个图形的周长，学生大多采用数、算的办法。几乎很少有人想到平移的方法，这时教师及时隐去了格子，“逼迫”学生寻找另外的方法进行比较。学生的思维得以深入，对周长的本质理解更为深刻。

3.移一移。

师：老师要将②号图形改变一下，我们再来比比周长，你同意哪个选项？

师：再变呢？

师：如果继续变，图形变得很小很小，很细很细呢？（师白板演示变化的图形）

师：你有什么发现吗？

生：图形的大小改变了，周长却一直不变。

生：图形的大小和周长没什么关系。

4.分一分。

师：②号图形的改变给同学们带来了很多启发与思考，现在老师要在①号图形中变变变了，如果把①号图形分成两个部分，它们的周长会相等吗？（生操作）

【评析】练习设计应该体现一定的层次性和灵活性。目的之一是夯实学生的基础，基础知识和基本技能是学生发展的根本，教学中不能淡化；另一方面让学生的思维走向深刻，着眼学生的后续发展。本节课的练习通过对图形的拼一拼、移一移、分一分等活动，引导学生在对比、辨析中加深对周长含义的理解。同时将周长与图形的大小等概念进行区别，为今后面积等概念的学习打好思辨基础。

四、找一找、说一说，回归生活与全课小结

1.周长在我们的生活中应用广泛，你能举出这样的例子吗？（头围与帽子等）

2.通过今天的学习，你有什么新的收获？

【评析】数学来源于生活并用于生活，将学生所学知识与熟悉的生活情境相关联，沟通了数学与生活之间的联系，让学生从数学的视角去观察生活、解释生活，激发学生学习数学的兴趣，获得数学学习的成功感。

（浙江省教育科学研究院附属小学 310000）