用数值方法分析两例力学问题

于志明

(连云港师范高等专科学校物理系，江苏 连云港 222006)



·问题讨论·

用数值方法分析两例力学问题

于志明

(连云港师范高等专科学校物理系，江苏 连云港 222006)

利用计算机进行数值计算来研究科学技术中的复杂问题,已经成为现代科学技术研究的一种重要方法.本文用两个例子来介绍比较复杂的力学问题的数值计算研究方法.

1 双振子弹簧系统运动的数值分析

文献[1]研究了图1所示的双振子弹簧系统中物体的运动问题.

图1

在图1中,物块A、B的质量相等,在物块A上施加一水平恒力F作用,物块B足够长,放置在水平地面上,所有接触面都是光滑的,轻弹簧开始处于原长,运动过程中始终处于弹性限度内,开始时物块A、B是静止的.求物块A、B运动的速度随时间的变化规律.

建立如图1所示的坐标系O-x,坐标原点在开始运动时B物块的左端点处.设某一时刻t,物块A、B的位置坐标分别为x1、x2,如图1所示.由牛顿第二定律得

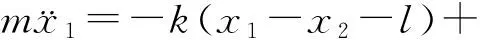
(1)

(2)

式(1)、(2)中的m为物块A、B的质量,k为弹簧的劲度系数,l为弹簧的原长.这是一道比较复杂的力学题,用数学分析的方法来求解比较难,但用数值计算的方法就比较容易.

以下是笔者利用MATLAB软件编写的计算程序:[2]

x1=1;x2=0;v1=0;v2=0;F/m=10;

k/m=50;

dt=0.001;

for j=0:1000

a1=F/m-k/m *(x1-x2-1);

a2=k/m *(x1-x2-1);

v1=v1+a1*dt;

v2=v2+a2*dt;

x1=x1+v1*dt;

x2=x2+v2*dt;

plot(0.001*j,v1, 0.001*j,v2,′r:′)

hold on

end

图2

图2与根据文献[1]中给出的物块A、B的速度与时间的关系式画出的曲线完全相同.

如果物块A、B的质量不同,如果有摩擦及空气阻力的作用,则数值计算的方法就会比数学分析的方法更有优势.图3是物块B的质量是A的质量的2倍时数值计算得到的结果.

图3

2 “猎犬追击狐狸”运动时间问题的数值分析

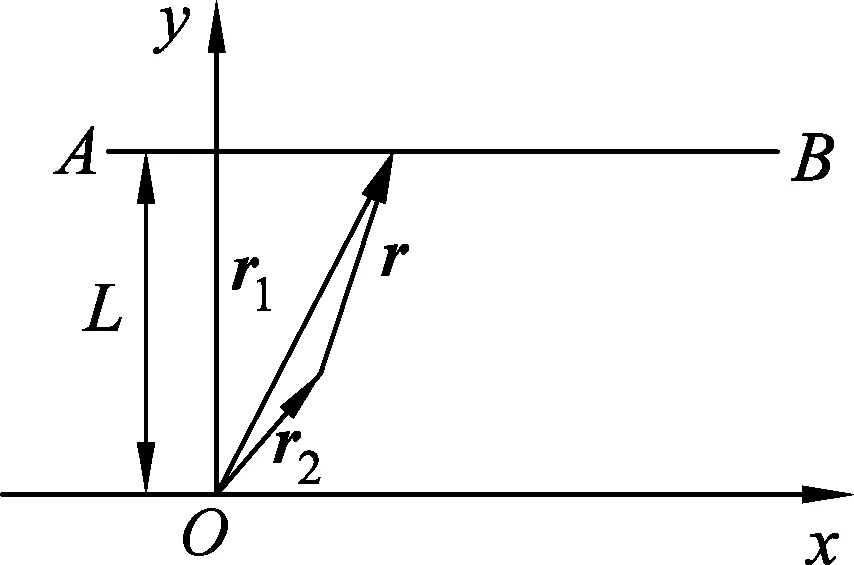
图4

文献[3]讨论了如图4所示的“猎犬追击狐狸”运动的时间问题.

在图4中,有一只狐狸以不变的速度v1沿直线AB逃跑,一猎犬以不变的速度v2追击狐狸,猎犬运动的方向始终指向狐狸.设开始时猎犬与狐狸的垂直距离为L.求猎犬追上狐狸的时间.

设狐狸相对于O点的位置矢量为r1,猎犬相对于O点的位置矢量为r2,狐狸相对于猎犬的位置矢量为r,显然r=r1-r2.由于r的方向就是猎犬运动的方向,故猎犬运动的速度可表示为

(3)

根据狐狸的运动知x1=v1t,y1=L.

由式(3)可得

(4)

(5)

如果能由式(4)、(5)求出猎犬的坐标x2、y2与时间t的关系式,利用猎犬追上狐狸时,y2=L,x2=v1t,就可以求得猎犬追击狐狸运动的时间,但用数学分析的方法是比较困难的,下边我们用数值计算的方法来解决.

本题数值计算方法的思路:取定v1、v2、L,从猎犬追击狐狸运动的开始时的x1、y1、x2、y2开始,让时间增加一个微小的量dt,由式(4)、(5)求出增加的dx2、dy2,将dx2、dy2加到之前的x2、y2上就得到了猎犬运动dt时间以后的位置坐标,然后再让时间增加一个微小的量dt,用同样的方法得到猎犬运动2dt时间后的坐标,如此循环下去,得到猎犬运动过程中各个时刻的位置坐标.

以下是用MATLAB软件编写的计算程序：

v1=10;v2=12; L=10;

x1=0;x2=0;y2=0; dt=0.001;

for j=1:3000

x1=x1+dt.*v1;

x2=x2+dt.*v2.*(x1-x2)./((x1-x2).＾2+(L-y2).＾2).＾0.5;

y2=y2+dt.*v2.*(L-y2)./((x1-x2).＾2+(L-y2).＾2).＾0.5;

plot(0.001*j,x2,0.001*j,x1,′-′)

hold on

end

在程序中取v1=10m/s,v2=12m/s,L=10m,dt=0.001s.由程序得到的狐狸和猎犬坐标x1、x2与时间t的关系曲线如图5所示.

图5

追击成功的条件是x2=x1,由图5可见,猎犬追击的时间约为2.7s.与文献[3]中的结果相同.

通过数值计算,我们还可以方便地得到猎犬追击运动的轨迹曲线如图6所示.

图6

根据数值计算的数据,可以画出各种关系曲线,拟合出各种变化的关系式.

1 韩忠全等.双振子弹簧系统两振子的速度-时间图像究竟是哪一个?[J].物理教师,2013,34(3):55-57.

2 彭芳麟等.MATLAB应用:论力学计算机模拟[M].北京:清华大学出版社,2002.

3 陈泽等.谈“猎犬追上狐狸的时间”另一求法[J].物理教师,2013,34(10):92.

2016-12-12)