课程难度研究综述

俞晓明 曹玉娟 谢 丽 李春密

(1. 盐城工学院,江苏 盐城 224051； 2. 北京师范大学物理学系,北京 100875; 3. 长江大学物理与光电工程学院,湖北 荆州 434023)



·教育理论研究·

课程难度研究综述

俞晓明1,2曹玉娟1,2谢 丽2,3李春密2*

(1. 盐城工学院,江苏 盐城 224051； 2. 北京师范大学物理学系,北京 100875; 3. 长江大学物理与光电工程学院,湖北 荆州 434023)

课程难度是当代教育理论与教育实践迫切需要解决的前沿难题,也是极其重要、极为复杂、极具挑战的综合性研究课题之一．本文分别从宏观层面和微观层面梳理了课程难度研究取得的成就,评析并指出两层面研究需要努力的建议．

课程难度； 宏观研究； 微观研究； 难度模型

1 引言

课程难度是当代教育理论与教育实践迫切需要解决的前沿难题,也是极其重要、极为复杂、极具挑战的综合性研究课题之一．课程难度研究的重要性体现在课程难度研究对揭示学习规律、指导课程教学、引领课程评价等具有理论科学价值和实践指导意义．课程难度过高,如赞可夫所倡导的“高难度”课程,学生在信息加工时的“认知负荷”过重,会阻碍学习,甚至扭曲身心健康发展;课程难度过低,如布鲁纳所倡导的“无难度”课程,学生在信息加工时的“认知负荷”过低,同样会延滞发展,甚至扼杀潜能的发挥．只有科学的、符合认知规律的课程难度,才会驱动学生“满负荷”地进行认知信息加工,实现学生健康和谐的发展．课程难度的复杂性体现在两个方面: 一是课程难度研究涉及的影响因素(如学习者、学习材料、学习环境等)很多,并且这些因素常常互相交织、互为作用;二是课程难度研究的影响因素难以精准刻画,难以受控和重复．课程难度研究的挑战性也体现在两个方面： 一方面因为课程难度的定义尚未有明确的、公认的界定,因此,出现说法各执一词、观点百家争鸣的蓬勃发展局面;另一方面驱动学生信息加工的微观机制和认知发生机理尚不清楚,探索的空间和潜力很大．

课程难度研究已具有一定基础: (1) 通过大量实践,课程开发者、教育管理者、教育者等对课程的理解业已深刻,对学习者的认知基础和学习材料的难度水平基本有比较准确的、定性的直觉,加之课程难度的描述量可通过设计合适的测查量表由学生的自我汇报和学业表现等而获得或验证．(2) 国内外学者早已意识到课程难度研究的重要性,并进行了大量的研究,取得了丰硕的实践成果．

本文通过对国内外课程难度研究工作的梳理发现,课程难度研究的焦点主要集中在宏观和微观两个层面．宏观层面的研究主要分3个阶段: (1) 区分不同课程(学科或学习材料)的难易度，以定性给出学习的次序,如中国古代先哲的论述. (2) 通过长期的躬耕实践，力图构建宏伟的课程体系,让不同年龄阶段的学习者“依梯而爬”,进而得到发展,如夸美纽斯、赞可夫等. (3) 寻求描述课程难度的特征量，致力于建构学习者在不同年龄阶段的发展量化模型,如黄甫全．微观层面的研究主要是寻求描述课程难度的特征量来建构具体课程(学科)的难度模型，以比较同一时期不同课程间的难度水平,如Daniel James Mundfrom、鲍建生、史宁中等．下面分别从宏观和微观两个层面对课程难度的研究工作进行梳理和评述,期待能为后续的研究架桥筑路，提供借鉴．

2 课程难度的宏观层面研究

课程难度的宏观层面研究分3个阶段,即区分不同课程(学科或学习材料)的难易度，以定性给出学习的次序； 构建宏伟的课程体系，让不同年龄阶段的学习者“依梯而爬”和寻求描述课程难度的特征量，以建构学习者在不同年龄阶段的发展量化模型．

2.1 学习内容难度定序的中国先哲论述

课程形成的历史是比较新的,但构成课程之基础的学科本身的历史却是古老的．聪慧的中国先哲早已注意到学习内容的难度问题并提出指导教学的著名论断．

墨子“子深其深,浅其浅,益(增益)其益,尊(撙节)其尊”,[1]意指教学必须因各人固有才资而施教,否则学生就会难以接受,并提出“量力所能至”的自然原则;《学记》“学不躐等”、“不陵节而施之谓孙”,[2]“不躐等”是说不要超越学习中的必经阶段,“不陵节”是指不要超越学生所能接受的限度,如果“杂施而不孙,则坏乱而不修”,教学必然导致失败;南宋朱熹“读书先读《大学》,以定其规模,次读《论语》,以立其根本,次读《孟子》,以观其发越,次读《中庸》,以求古人之微妙处”、“以二书言之,则通一书而后及一书;以一书言之,篇章句子,首尾次第,亦各有序而不可乱,量力所至而谨守之．字求其训,句索其旨,未得乎前,不敢求于后;未通乎此,不敢志乎彼．如是则志定理明,而无疏易陵躐之患矣”[3]等皆说明学习要循序渐进,要注意学习的难度梯度．

如将《大学》、《论语》、《孟子》和《中庸》看成中国的古代课程,则早在八百多年前的南宋理学家朱熹就已根据课程难度规约了学习次序．

2.2 西方的结构课程体系

不管是《大学》、《论语》、《孟子》还是《中庸》,这只是不同学者的论述集大成,朱熹只是为儿童学习“定其序”,并未根据儿童的身心发展规律而量身“定制”课程．夸美纽斯、赞可夫、布鲁纳等长期躬耕实践，力图构建课程体系以期让不同年龄阶段的学习者“依梯而爬”,进而得到发展．

(1) 夸美纽斯的自然主义课程结构论.

捷克教育家、课程论创始人夸美纽斯在其著作《大教学论》中指出: “课程具有内在秩序,这种结构秩序尽管是人为的,却是符合自然的．”[4]他认为课程内部结构秩序的特征是一道“排列得合适、数目充足、坚固安全的阶梯”,学习的特征就是爬阶梯．科目(课程)应当是难的,如果学生领会不了“并不能证明人类的心智有什么达不到的目的,只是证明阶梯排列得不好,……,只要有了排列得合适,数目充足,坚固安全的阶梯,无论什么人都是能够达到他所希冀的高度,这是一件毫无疑问的事实”．[4]他还认为课程内部结构秩序具有一种潜力,这种潜力表现为“难”, “难”促进人潜在智慧的显露．事物作用的潜力,其实质“是由于秩序的万能的支配力而已，这就是说,力量的发生是由于把一切有关部分按照它们的数目、大小和重要程度安排起来．”[4]“只要它能保持它的秩序,它就可以保持它的地位和力量．”[4]

课程结构秩序应与学生的年龄特征和起点水平相适应．夸美纽斯认为“一切应学的科目都应加以排列,使其适合学生的年龄”、[4]“各个班级的一切功课都应仔细分成阶段,务使先学的为后学的扫清道路,给与解释”、[4]“(学校的)全部期间应当分成4个明显的阶段,即婴儿期、儿童期、少年期和青年期,我们应给每期分派6年的光阴和一种特殊的学校”，“这些不同的学校不是要去研究不同的学科,而是要用不同的方法去学习同样的学科”，“自始至终要按学生的年龄及其已有的知识循序渐进地进行教导”．[4]

夸美纽斯受英国哲学家培根的唯物主义哲学的影响,认为一切事物都受自然秩序所制约,倡导教学工作要适应自然秩序的原则．他已意识到学校教育必须考虑儿童的特点和成长的阶段性,主张把“一切事物”教给一切人,并认为教育就是“把一切事物教给一切人们的全部艺术”．夸美纽斯通过长期对教学的实践和对儿童进行的观察,建立了年龄期的划分及与之相应的学校类型的宏伟教育学体系,把教育学从哲学中解脱出来,为人类的教育事业做出了丰功伟绩．他的自然主义课程结构论同他的教育理论一样闪耀着那个时代的光辉,为现代课程理论的发展奠定了理论基石．尽管他隐隐约约感觉到学校课程难度的存在,但由于未能依靠科学心理学的事实,仍“未能站到‘难度’的高度来概括课程内部结构秩序的实质”．[5]

(2) 赞可夫的“高难度”课程观.

苏联教育家、心理学家赞可夫提出包含“高难度”、“高速度”在内的5条教学原则．他指出:“在我们实验体系的教学论原则中,起决定作用的是以高难度进行教学的原则．‘难度’这个概念,在教学论中使用于各种不同的场合,具有各种不同的含义．这个概念的涵义之一,是指克服障碍．……这个概念的另一个涵义,是指学生的努力”、“以高难度进行教学的原则的特征,并不在于提高某种抽象的‘平均难度标准’,而是首先在于展开儿童的精神力量,使这种力量有活动的余地,不能够给以引导．如果教材和教学方法使得学生面前没有出现应当克服的障碍,那么儿童的发展就会萎靡无力”，“以高难度进行教学,能引起学生在掌握教材时产生一些特殊的心理活动过程”、“难度的程度要靠掌握难度的分寸来调节．……按照我们的理解,难度的分寸绝不是要降低难度,而是合理地运用这一原则的必要因素．……难度的分寸具体体现在教学大纲、教科书、教学法指示和教学方式里,它在日常教学工作中还取决于教师经常留意儿童掌握知识和技巧的过程和结果”．[6]

赞可夫的系统研究触及了教育的实质——课程难度．他的研究工作以教育学理论为指导、以维果茨基“最近发展区”等心理学理论为依靠,在长期躬耕教学实践过程中逐渐形成的“实验教学论体系”是教学与发展问题的实践经验和理论总结,充满时代精神,富有创新意义．然而他的工作也存在诸多问题难以回答,如高难度究竟如何科学量化、高难度置学生其他能力的培养于何处、置学生的积极性和主动性的发挥于何处等等．

(3) 布鲁纳的结构主义课程论.

美国结构主义课程论专家布鲁纳认为，“课程,不仅反映知识本性本身,也反映认识者本性本身,而且也反映认识者本性和掌握知识过程的本性”．[7]知识的本性是学科内容的组织结构问题;认识者本性就是儿童认知结构的发展、认识方式的问题;掌握知识的过程就是教学过程,亦即发现、探究的过程．对教育最具重要性的是“学科的基本结构”,即“基本的原理、基础的公理和普遍性的主题”．[8]“没有难教难学的知识”,“任何学科都能够以某种智育上适宜的方式教给任何发展阶段的任何儿童”．[8]

布鲁纳受结构主义的影响,将自然科学方法引入课程论研究,倡导了知识结构、学科结构的理论,在课程编制上具有极大的启示意义．他提出的“学科的基本结构”成为美国“返回基础”教育运动的主要思想;提出“螺旋型课程”的概念及其“连续性和发展性”特点,既保证课程“直线式”的优点,也继承课程圆周式的心理组织方式．尽管“螺旋式课程”曾经作为一种课程思潮,对美国教育乃至世界教育都产生了深远影响,但由于布鲁纳忽视了儿童的智力活动和成人的智力活动之间的差异,倡导的教材难度远远脱离教学实际,教材内容也远远脱离实际需要, 因而遭受挫败．这些都警示我们课程结构在注意学科知识结构的同时,更多地要注意社会的需要．

2.3 阶梯型课程量化模型

黄甫全基于课程的概念给课程难度下了一个定义,“在我看来,课程难度是预期的教育结果从简单到复杂、从低级到高级的质和量在时间上相统一的动态进程”．[5]作用于课程难度的因素主要有3个:一是社会发展的要求与可能;二是人的发展的要求与可能;三是人类知识的发展及其体系结构．这3个因素既分别地制约着课程难度,又综合地决定着课程难度．从整体上看,课程难度是一种动态进程;从教育活动的发展进程看,课程难度发生着由低级到高级的相对快速的上升．根据活动进程,课程难度可分为幼儿园课程难度、小学课程难度、中学课程难度、大学课程难度和大学后课程难度;根据课程结构化程度和组织化程度的高低,课程难度分为显性课程难度和隐性课程难度,并且侧重探讨的中小学校的显性课程难度．他还认为课程是一个非常特殊的灰色系统,具有最大程度的可控制性．他以0～11岁儿童的脑电频率为课程难度的映射量,基于灰色系统理论的动态模型建构方法和步骤,建立了课程难度的均值灰色模型、低值灰色模型和高值灰色模型,并根据后验差检验的原理和计算方法,检验了各模型的精度,精度均为最高等级．[5]各模型如下.

(1) 课程难度均值灰色模型.

XA(k+1)=141.2740e0.0422k-136.6540.(0≤k≤11)

(2) 课程难度低值灰色模型.

XL(k+1)=108.9348e0.0437k-105.4348.(0≤k≤11)

(3) 课程难度高值灰色模型.

XH(k+1)=199.0229e0.0371k-193.5229.(0≤k≤11)

学科要成为科学必须要建立一定数量的、可量化的、可测量的、可验证的概念或模型．物理学之所以成为近代自然科学的典范,就在于物理学是由大量可量化、可测量的概念以及由概念间的联结而成的、可为实验验证的规律组成的体系．难度可作如下诠释,“难”本是困难、艰难,是困难程度的定性化描述;“度”本是哲学概念意指事物质与量之间的临界值,是量化刻画的数值．因此,课程难度研究要科学化就必须建立科学化的课程难度量化模型．建构课程难度的定性模型或许简单,但寻求特征量以定量化研究着实困难．国内黄甫全博士(1995)建构了中小学课程难度的均值指标灰色动态模型、中小学课程难度的低值指标灰色动态模型和中小学课程难度的高值指标灰色动态模型体系，具有一定的科学性和实用性,3个数学模型从量的层面揭示和规范了课程难度在广度、深度和进度上与学生发展水平相适应的立体统一的动态进程,为课程难度比较、课程研制、教材编写等提供了技术性手段．更为可喜的是他的工作掀起了科学地、系统地研究课程难度的高潮,其建构课程难度模型的思想也得到了长足发展．

3 课程难度的微观层面研究

课程难度的宏观层面研究方向主要研究不同年龄段儿童的依次发展,而课程难度的微观层面研究方向则独辟蹊径主要研究同一年龄段不同课程间的课程难度或同一年龄段不同区域(或不同版本)同一课程间的课程难度问题．课程难度微观层面研究继承和发展了宏观层面研究者们寻求描述课程难度特征量建构量化模型的思想,并不断地得以修润和完善．

3.1 课程难度微观模型的雏形

Daniel James Mundfrom(1991)在博士论文中提出用学生难度评估、学生入学时的ACT或SAT成绩、大学课程平均分以及大学课程对学生的要求这4个特征量来评估大学课程间的相对课程难度．[9]他的研究分为2个阶段：第1阶段首先证实“学生难度评估”这个特征量的可靠性,接着研究不同性别的测试者、不同年级的在校学生对40门大学课程的相对课程难度进行评估排序；第2阶段首先对第1阶段获得的评估数据进行描述性分析,接着考查“学生难度评估”、“学生入学时的ACT或SAT成绩”、“课程平均分”这3个指标的可靠性,最后将评估的课程从40门扩充到50门．

3.2 课程难度微观模型的发展

刻画课程难度是困难的,科学量化课程难度则更为困难．Daniel James Mundfrom提出用“学生难度评估”、“学生入学时的ACT或SAT成绩”、“大学课程平均分”以及“大学课程对学生的要求”来刻画课程难度,自此吸引了国内很多学者参与到这一项极具挑战性的研究课题,课程难度微观模型也得到了长足的发展．典型的有鲍建生基于“背景”、“运算”、“推理”、“知识含量”和“探究”的综合难度模型和史宁中等人基于课程深度、课程广度和课程时间的课程难度模型．其中,以史宁中等人建构的课程难度模型影响力最大,在此基础上修缮改进的模型也最多．

(1) 鲍建生的综合难度模型.[10]

鲍建生借鉴了Nohara(2001)总体难度概念涉及到的4个难度因素——“扩展性问题”的百分比、含有“实际背景”题目的百分比、包含“运算”题目的百分比(不包括属于“数量”部分的题目)和包含“多步推理”题目的百分比．针对国内数学课程教学实际情况,将“背景”、“运算”、“推理”、“知识含量”和“探究”作为数学课程综合难度模型的5个主因素,并根据层次性和可操作性对各个具体数学题的难度水平进行赋值,然后用加权平均的方法对每个因素给出一个量化的指标．计算公式为

其中di(i=1,2,3,4,5)依次表示“探究”、“背景”、“运算”、“推理”和“知识含量”5个难度因素的取值;dij为第i个难度因素的第j个水平的权重(依次取1、2、3、…);nij表示这组题目中第i个难度因素的第j个水平的题目的个数,其总和等于该组题目的总数．综合难度因素的水平划分如表1所示．

表1 鲍建生数学课程综合难度因素水平划分

根据前面所得到的5个值dij(i=1,2,3,4,5)画出反应课程综合难度的五边形模型(雷达图),并根据图像的整体势态分析课程的综合水平与难度特征．

(2) 史宁中等课程难度模型.

史宁中等人认为影响课程难度的基本要素至少有3个,即课程深度、课程广度和课程时间,并建立了课程难度模型．他们用N、S、G分别表示课程难度、课程深度和课程广度,用T表示课程时间;定义单位时间的课程深度S/T为“可比深度”、定义单位时间的课程广度G/T为“可比广度”,并用“可比深度”和“可比广度”的加权平均来刻画课程难度．[11]课程难度模型为

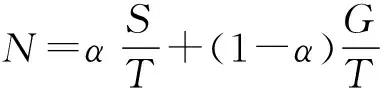
其中α满足0<α<1,称为加权系数,反应课程对于“可比深度”或“可比广度”侧重程度．

基于构建的难度模型,史宁中等比较了2001《课程标准》与1963《教学大纲》和2000《教学大纲》中“三角形”等几何内容的课程难度,结论是2001《课程标准》有关课程内容的课程广度稍有增加,课程深度也稍有增加,但是,由于课程时间降低的幅度过大,导致课程内容的可比深度和可比广度都在普遍加深、加大,课程非但没变容易,反而变难了;比较了“三角函数与解三角形”有关内容的课程难度,结论是对于“圆”来说, 1963 年、2000 年、2001 年的课程难度N1、N2和N3满足关系N3>N1>N2,即2001 年相应的课程内容最难,2000 年最容易．

尽管该模型存在着这样那样的瑕疵,但后续学者大都在此模型的基础上进行修缮和改进．

① 任晓峰课程难度模型.[12]

任晓峰沿袭史宁中等人的课程难度模型,仍然用课程的知识含量,即用课程含有“知识点”的多少来衡量课程广度．改进了的是根据课程目标对知识内容的要求程度，即对课程深度进行加权赋值,每个知识点的深度由低到高分为 4 个水平:了解、理解、掌握、灵活运用,权重分别为 1、2、3、4,利用如下公式计算课程深度，

② 仲扣庄课程难度模型.[13]

仲扣庄等利用史宁中课程难度模型在对课程标准、各版本教科书中理论部分的知识点及其深度赋值时发现:对广度和深度赋值时两者数值相差很大(10倍以上),在定量分析时α通常取为0.5,导致内容深度主要由广度决定．

因此定义相对可比深度Xn、相对可比广度Yn,以进行定量表征．Xn、Yn的定义为

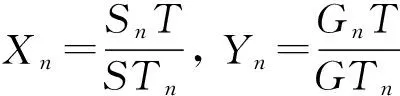
其中S、G、T分别表示课程深度、课程广度和课程进度,Sn、Gn、Tn、Xn、Yn分别为各版本教科书的深度、广度、进度、相对可比深度、相对可比广度．

相对难度的函数关系式为

N′=αX+(1-α)Y.

③ 范佳午课程难度模型.[14]

范佳午等保留了孔凡哲关于“基础教育课程基础性、普及性和发展性的要求,系数α应取0.5为宜,即课程不宜过广过浅,也不宜过窄过深”的观点,在应用史宁中的课程难度模型进行高中物理教科书难度评价时发现“原模型没有在广度与深度之间做适当的平衡”．于是定义了两个平衡系数m、n,使课程标准的广度值和深度值均达到1,再在确定的m、n值下,计算各版本教材的难度并进行比较．

修改的课程难度定量模型为

其中m、n由课程标准的广度值和深度值决定．

④ 蔡庆有的改进模型.[15]

蔡庆有等借鉴了鲍建生课程综合难度模型的核心(解题)和史宁中等课程难度模型的核心(课程标准对数学内容的规准),提出在课程时间基本一致时的小学数学教材难度模型,该模型可表述为

N=0.77C1+0.91W+0.86E，

C=0.84C1+0.59C2+0.42C3，

W=0.89W1+0.67W2+0.69W3，

E=0.75E1+0.71E2+0.74E3.

将格式标准化可近似表示为

N=0.30C+0.36W+0.34E，

C=0.45C1+0.32C2+0.23C3，

W=0.40W1+0.30W2+0.30W3，

E=0.34E1+0.32E2+0.34E3.

其中N表示小学数学教材难度,C表示内容难度,W为例题难度,E为习题难度;C1表示内容多少，C2表示内容要求，C3表示内容呈现方式;W1表示例题要求，W2表示例题与内容的切合度，W3表示例题复杂度;E1表示习题与例题匹配，E2表示习题题型，E3表示习题要求．

⑤ 郭民的改进模型.[16]

郭民等在史宁中课程难度模型的基础上,引进了“知识团”(知识点的结合和知识点之间的组合)的概念,同时将正文与习题分开研究,构建了课程难度模型为

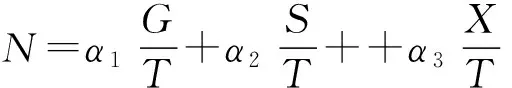
其中N表示知识团的难度,G表示知识团的广度,S表示知识团的深度,X表示习题的综合难度,T表示学生学习该知识团的总课时,α1、α2和α3分别表示知识团的可比广度、可比深度、可比习题综合难度的权重．

郭民等认为,知识团主要由概念和命题组成,知识团的广度即知识点的总和．他们将组成知识团的概念按“白描、归纳类比、抽象定义”3个深度水平分别赋值1、2、3;将命题按“了解、理解、应用”3个深度水平分别赋值1、2、3;将习题按“习题性质、习题背景、知识点含量”3个维度分别赋值权重0.4、0.4、0.2．其中,习题性质按“模仿、迁移与应用、探究”分别赋值1、2、3;习题背景按“无背景、生活与公共常识背景、科学背景”分别赋值1、2、3;知识点含量按“1个知识点、2～3 个知识点、4个及以上知识点”分别赋值1、2、3．

4 课程难度研究的评述

将课程难度的研究分为宏观和微观两个层面，只是源于课程的概念“至今没有达成能够得到人们公认的结果,不仅缺乏具有普遍性的科学定义,甚至没有形成若干便于人们使用和沟通的工具性定义”[17]而主观提出的,并且认为它们只是课程难度研究的两个不同层面,二者实质上存在着内在关联．宏观层面的研究架构并划分了微观研究的不同阶段,绘制着课程发展的宏伟蓝图;微观层面的研究则是宏观研究的细实化、丰润化,二者互为补充,不可或缺．尽管课程难度这两个层面的研究均已取得丰硕成果,但仍存在着发展空间和改进之处．

4.1 宏观层面研究的努力方向

课程难度的宏观层面研究顺应了课程发展的总体要求,绘制着课程发展的宏伟蓝图,指导、调节并架构了课程体系和体系的发展．夸美纽斯、赞可夫和布鲁纳等的可贵之处在于它们多年的执着坚守、长期的躬耕实践,在大量观察事实的基础上将实践经验总结并上升为理论．黄甫全基于灰色系统理论和概率统计方法,利用儿童脑电频率这一心理发展变量作为课程难度描述的特征量建构了课程难度模型,使得课程难度成为理想的、科学的和令人信服的结构模型．

然而随着科学的蓬勃发展和新精技术在教育学、心理学以及认知神经学的广泛应用,反映心理发展的变量也远远超出脑电频率这一特征量,寻求更准确、可靠的心理、生理特征量以建构更为科学的课程难度模型理应成为课程难度宏观层面研究的发展方向．

4.2 微观难度层面研究的努力方向

虽然国内外课程论专家早已关注到课程难度问题,但真正开始量化刻画课程难度还是从近些年来中小学理科教材的国际化比较开始的,研究的目的主要是科学回应社会广泛关注的课程负担问题,因此课程难度的微观层面更多地侧重于教材这一静态文本的难度比较．

尽管课程难度微观层面的研究业已找到了相关的特征量来建构模型以刻画课程难度,但仍然存在需要努力的空间．

(1) 课程难度的界定还只停留在操作定义层面,研究的目的还仅限于难度量值的确定和难度量度的比较,尚未科学阐述难度量值的具体涵义.

(2) 课程难度模型中的时间用的是由《课程标准》等规定性文件中所建议的学时数,并未将学生课外学习的时间纳入课程难度模型.

(3) 课程难度研究还仅仅局限在教材这一静态文本的单因素上,而且难度比较以知识点或知识团为单元进行赋值,其“颗粒度”还过于宏观.

(4) 课程难度研究尚未涉及课程的教学过程、尚未触及学生的学习过程,因而无法通过课程难度来真正揭示教学规律和学习规律．

事实上,课程是由系列概念以及由概念间的联结而形成的规律所组成,在概念框架理论下建立概念及概念间的联结均需要认知主体进行信息加工,概念及概念间的联结不同,彼此信息加工的认知负荷各不相同．因此,建立基于认知负荷模型的课程难度模型很必要,也值得期待,这说明课程难度研究还存在广阔的空间．

诚然,课程难度是由教材本身、学生实际、教师教学过程以及教学环境等众多因素交织影响的应变函数,课程难度研究本身也是“高难度”问题．以往评估课程难度主要靠专家的主观判断、一线教师的教学体会和学生的学习感受,只能给出大致定性的结论．尽管如此,先验的课程难度结论也为后续课程编制、教材编写提供了宝贵意见,使得教材不断符合教师教学需要和学生学习要求．定量与定性研究的结合是社会科学取得突破性成就的表现．值得庆幸的是自黄甫全课程难度灰色系统模型,尤其是史宁中课程模型建立以来,课程难度的研究已走上定量研究的康庄大道,这理应成为课程评估科学发展的标志．

1 安树芬,彭诗琅.中华教育通史[M] (第1卷).北京： 京华出版社,2010： 230.

2 于洪卫,王洪军.中国传统思想[M].东营： 石油大学出版社, 1992：230.

3 高奇.中国高等教育思想史[M] (第2版).北京： 人民教育出版社，2001：121，123.

4 夸美纽斯著,傅任敢译.大教学论[M].北京： 人民教育出版社，1979：64,71，73，88,97，230-231.

5 黄甫全(1996).阶梯型课程引论:关于中小学课程难度的研究[M].贵州： 贵州人民出版社,1996： 20-21,27-28,174-190.

6 赞可夫编,杜殿坤,张世臣等译.教学与发展[M].北京： 人民教育出版社,1985: 41-51.

7 钟启泉.现代课程论[M].上海： 上海教育出版社，1999：134.

8 J Bruner.The Process of Education[M].Harvard University Press (Cambridge)，1977： 22,52-54.

9 D J Mundfrom. Estimating course difficulty. Retrospective Thesis and Dissertations[D].Iowa state univ.,1991： 9560.

10 鲍建生.中英两国初中数学期望课程综合难度的比较[J].全球教育展望，2002，31(9)：48-52.

11 史宁中,孔凡哲,李淑文.课程难度模型:我国义务教育几何课程难度的对比[J].东北师大学报(哲学社会科学版)，2005，218(6)：151-155.

12 任晓峰.中国新加坡两国高中微积分课程难度的比较研究[D].苏州大学,2009：20-23.

13 仲扣庄,郭玉英.高中物理课程标准教科书内容难度定量分析——以“量子理论”为例[J].课程·教材·教法,2010，30(4):5,67-71.

14 范佳午,郭玉英,黄福,谭晓.高中物理教材“运动描述”内容难度定量分析[J].内蒙古师范大学学报(教育科学版),2012,25(6):115-117.

15 蔡庆有,邝孔秀,宋乃庆.小学数学教材难度模型研究[J].教育学报,2013(5):97-105.

16 郭民,史宁中.中英两国高中数学教材函数部分课程难度的比较研究[J].外国中小学教育,2013(7):55.

17 丛立新.课程论问题[M].北京： 教育科学出版社,2001：1-2.

2017-01-26)

* 通讯作者：李春密(1966— )，北京师范大学物理学系教授，博士生导师，主要从事物理课程与教学论、物理教育与心理发展、中学物理实验教学研究.E-mail: licm@bnu.edu.cn.