数学核心素养在小学教学中如何落实
◇顾 沛
数学核心素养在小学教学中如何落实
◇顾 沛

近两年,各种媒体上关于“核心素养”的讨论相当丰富,核心素养逐渐成为中小学素质教育的一个抓手。教育部立项研究的核心素养,包括两个方面,或者说两个层次:一个是学生发展核心素养,一个是学科核心素养。学生发展核心素养的研究结果,教育部已经于2016年9月13日公布并征求意见;高中近20个学科的学科核心素养的研究已经告一段落,预计结果会在2017年第一季度随《高中课程标准(修订稿)》的公布同时出炉。
学生发展核心素养是指“学生应具备的,能够适应终身发展和社会发展需要的必备品格和关键能力”,从“自主发展、社会参与、文化基础”三个方面展开,目标是“培养德、智、体、美全面发展的社会主义事业建设者和接班人”。学生发展核心素养以文化基础的积累和自主发展能力的提升为支撑条件,引导学生在社会参与及互动过程中践行社会主义核心价值观。
高中阶段数学学科的核心素养虽然目前尚未公布,但从目前的研究看,主要包括以下6个素养,分别是:数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析。笔者认为,小学阶段数学学科的核心素养,与高中应该是相通的,不需要另起炉灶、再行研制,也即:小学阶段数学学科核心素养与高中是相同的,也是上述6个。
本文主要讨论数学学科的6个核心素养在小学教学中如何落实,也附带涉及学生发展核心素养。
一 数学核心素养的含义
数学核心素养是具有数学基本特征的、适应学生个人终身发展和社会发展需要的人的思维品质与关键能力。上述6个核心素养的定义,或者说“解释”如下所示。
“数学抽象”是指舍去事物的一切物理属性,得到数学研究对象的素养。主要包括:从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系,从事物的具体背景中抽象出一般规律和结构,用数学语言予以表征。
“逻辑推理”是指从一些事实和命题出发,依据规则推出其他命题的素养。主要包括两类:一类是从特殊到一般的推理,推理形式主要有归纳、类比;另一类是从一般到特殊的推理,推理形式主要是演绎。
“数学建模”是对现实问题进行数学抽象,用数学语言表达问题、用数学知识与方法构建模型解决问题的素养。主要包括:在实际情境中从数学的视角发现问题、提出问题,分析问题、建立模型,求解结论,验证结果并改进模型,最终解决实际问题。
“直观想象”是指借助几何直观和空间想象感知事物的形态与变化,利用图形理解和解决数学问题的素养。主要包括:借助空间认识事物的位置关系、形态变化与运动规律;利用图形描述、分析数学问题;建立数与形的联系,构建数学问题的直观模型,探索解决问题的思路。
“数学运算”是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养。主要包括:理解运算对象,掌握运算法则,探究运算思路,选择运算方法,设计运算程序,求得运算结果等。
“数据分析”是指针对研究对象获取数据,运用统计方法对数据进行整理、分析和推断,形成关于研究对象知识的素养。主要包括:收集数据,整理数据,提取信息,构建模型,进行推断,获得结论。
这6个核心素养并不是相互分离的,而是有密切联系的。笔者认为,它们可以分为三组,而且可以用下面的一段话表述它们之间的联系:我们要让学生学会用数学的眼光观察世界,发展数学抽象和直观想象的素养;让学生学会用数学的思维分析世界,发展逻辑推理和数学运算的素养;让学生学会用数学的语言表达世界,发展数学建模和数据分析的素养。这是因为,直观想象也是一种数学抽象,数学运算也是一种逻辑推理,数据分析也是一种数学建模。
二 数学核心素养在小学数学教学中如何落实
上述6个核心素养,是数学教学中的精髓。那么,这些核心素养如何在小学数学教学中落实呢?根据小学生的特点和小学数学教育的特点,笔者有下面一些思考,与大家分享。
小学数学的内容主要有识数、运算、图形、几何和推理,还有一点统计。“数”的概念形成依靠抽象,“图形”的概念形成也依靠抽象。例如,“5”是从5个野果、5条鱼、5颗石子等客观事物中抽象出来的;“圆”是从太阳、月亮、车轮等客观事物中抽象出来的。客观世界中并没有抽象的“5”和抽象的“圆”,数学的研究对象其实是人类思维的产物。“抽象”一词本身也是抽象的。到小学几年级可以在教学中对学生说“抽象”一词?这是一个可以研讨的问题。笔者觉得,从小学一年级起就可以,例如,在讲“5”和“圆”的概念时,就可以说上面的那些话,自然就带出“抽象”一词。在教师第一次或第二次讲“抽象”一词时,学生未必理解,可能只是生硬地接受;但是多次以后,学生慢慢就体会、理解了。小学生对“抽象”一词的理解,也许更多地靠数学课,而不是靠语文课。
“逻辑推理”一词及相应的素养也是从一、二年级开始就可以教给小学生,只不过起初可以只说“推理”,到高年级条件成熟时再表述为“逻辑推理”。例如,计算9+3=12时,有一个先把3拆成1+ 2的过程,再得出9+3=9+1+2=10+2=12。这种“算理”其实就是一种“推理”。当然,随着年级的升高,学生会逐渐接触一些稍复杂的推理。
“数学建模”的素养在三年级以后就可以教给小学生,只不过小学阶段可以不出现“数学建模”的说法,只说“模型”或者“类”等,最初甚至可以只用“一般形式的表达”的说法。例如,在学生学到加法交换律、乘法交换律时,可以说“这是对于所有的数都正确的等式,是普遍的规律,这是数学概括和总结的结果,我们应该重视这种一般形式的表达”。到高年级学到 “总价=单价×数量”“路程=速度×时间”等公式时,可以进一步说“这种一般形式的表达,也称为解决一类问题的模型”。
“直观想象”一词从字面上不易理解,因为它其实是“几何直观与空间想象能力”缩减字数的结果。笔者觉得,在小学阶段可以不出现“直观想象”一词,起初只分别用“直观”“想象”的说法,把相应的素养教给学生,到高年级再视学生的情况结合实例分别用“几何直观”与“空间想象能力”的说法。例如,《义务教育数学课程标准(2011年版)》(以下简称《课标》)“附录2”中的例32是:
观察图1(《课标》中的图8):
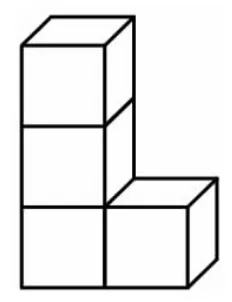
图1
请在图2(《课标》中的图9)中指出从前面、右面、上面看到的相应图形:
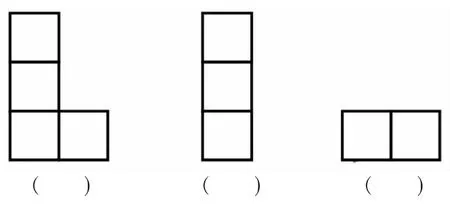
图2
对于该例的教学,教师可以为学生提供相应的实物,但是要避免在一开始就展示实物,因为那样会部分失去培养学生“直观想象”能力的机会,减少了教学过程中的思维含量,应该让学生在说出答案之后观察实物,作为对学生思维结果的“验证”。
“数学运算”一词及相应的素养可以较早教给小学生,起初可以只说成“运算”。“运算”本身虽然是抽象的,但由于小学生很早就学习了加法、减法等具体的运算,所以对“运算”一词他们并不陌生。这一核心素养的教学,不但需要关注学生运算的正确率和速度快慢,更要关注其运算方法的选择和对算理的了解。上面曾经举过一个9+3=12的例子,下面再简单说说除法运算的例子。在中低年级,数的范围局限在非负整数,除法只表示“平均分”,教学比较单一;到了高年级,数的范围扩大为整数、分数、小数,这时除法运算的教学在“平均分”以外也要扩大到“除法与分数的关系”“除法与比的关系”等。
“数据分析”一词及相应的素养在五年级学习平均数以后才可以教给小学生,之前学习各种统计图时可以用“数据收集”“数据整理”的说法。在三年级及以前应该让小学生经历简单的数据收集和数据整理的实践,但在这样的实践中最好不提“数据收集”“数据整理”这种专业词汇,只分别提及“数据”“收集”“整理”这些词。因为在三年级及以前,《课标》只要求学生“感受、体会数据蕴含信息”。
小学生初步习得这些核心素养,就具有了相应的文化基础,同时也在成长的道路上迈出了自主发展的步伐,也就获得了初步的学生发展核心素养。
我们在提倡培养学生核心素养的时候,要全面地、辩证地看问题,不能脱离知识的传授和建构孤立地谈论核心素养的培养。培养核心素养与传授数学知识不是分离的,更不是对立的,而是统一的、融合的。数学核心素养虽然是教学中的精髓,但是不能脱离知识“肉体”而存在。核心素养一定是以知识为载体传授的,而且不是在讲授知识时生拉硬扯、牵强附会地传授的,而是融入其中、因势利导、水到渠成地传授的;也不是摆开架势、长篇大论地传授的,而是潜移默化、画龙点睛地传授的。
例如,教师可以在“认识周长”的教学中传授或者渗透“数学抽象”的素养。“周长”是一个抽象的概念,它有四个核心要素——封闭图形、外围、一周、长度(数量)。教师如果从特殊到一般,从感性到理性,引导学生逐步归纳、概括、理解了周长的这四个核心要素,笔者觉得就是在传授知识的同时渗透了“数学抽象”的素养。但是笔者在听课时曾经听到教师说 “请同学们摸一摸课本封面的周长”这样的话,这就把“一周”与“周长”混淆了,周长是一个数量,摸是摸不出来的。所以,核心素养的培养一定是以正确的知识传授为载体的。
再例如,教师可以在“41个人两两握手问题”的教学中传授或者渗透“逻辑推理”的素养。例如,教师让学生从2个人两两握手、3个人两两握手开始思考,再到4个人、5个人两两握手等。在思考中,学生很快就会总结出“n个人两两握手,一共握了次”的规律。教师只要稍加提炼,说“这就是从特殊到一般的归纳推理”,就在讲授知识的同时渗透了“逻辑推理”的素养。
再例如,教师可以在“植树问题”的教学中渗透“数学建模”的素养。教师在教学中可以归纳,植树问题一共就分为那么几“类”:两端都种、两端都不种、只有一端种、围成一圈种。小学阶段可以不出现“模型”“建模”等词汇,而用通俗的“类”来代替,也同样渗透了“数学建模”的素养。在某些小学,如果时机成熟,教师也可以说:这样的“类”,在数学上也称为解决实际问题的“模型”。
再例如,教师可以在“小数加减法”等运算的教学中渗透“数学运算”的素养。比如,教师提出问题“做小数加减运算时,为什么小数点要对齐”后,在课堂上放手让学生探索、讨论。教师在适当火候因势利导、提炼总结,表述出:“两个数做加减时,每一次加减时单位一定要统一;小数点对齐后,十分位的单位都是0.1,百分位的单位都是0.01,等等。”这就把运算程序的教学提升到算理的高度,从而也就在讲授知识的同时渗透了“数学运算”的素养。
再例如,教师可以在“长方体的表面积”教学中渗透“直观想象”的素养。教师在展示实物,并提出“如何求一个长方体纸盒的表面积”的任务后,不应急于剪开该纸盒,而应引导学生观察长方体纸盒,逐渐用学生自己的语言表述出“长方体纸盒上、下、前、后、左、右6个面的面积之和,是该长方体纸盒的表面积”;然后剪开纸盒,在展开图上标出上、下、前、后、左、右,检验刚才的结论。这样的教学过程,就在讲授知识的同时渗透了“直观想象”的素养。如果能够引导学生建立纸盒实物、立体图与展开图中各个面的对应关系,就更好了。
再例如,教师可以在“阅兵问题”的教学中渗透“数据分析”的素养。在数据分析内容的教学中,数据最好是真实的、有意义的。比如,教师可以在播放阅兵仪式的录像片后,在黑板上展示阅兵中相关的数据,同时引导学生提出问题。例如,阅兵式要求每分钟走112步,1步长75厘米,问:平均1秒走多少米?再如,劳模方队的长度是27.9米,检阅区的长度是96米,问:劳模方队通过检阅区需要多少秒?这些都是有价值的真实问题。在解决问题的教学过程中,也渗透了“数据分析”的素养。
最后这个例子中,也可以借“阅兵仪式”“劳模方队”顺便进行思想教育,进行学生发展核心素养的教育。所以,依托学科教学,不仅能够培育学生的学科核心素养,而且也可以让学生发展核心素养的教育落地。作为数学教师,无论是小学教师、中学教师还是大学教师,从“育人为本”的理念出发,都有必要深入思考:数学学科的本质是什么?数学课程到底应该教给学生什么?数学学科的育人价值究竟在哪里?现在在高中课程标准修订的工作中,在认真地研究、表述各个学科的学科核心素养和学业质量标准时,将会进一步把“以知识为导向的教学”转变为“以核心素养为导向的教学”。
我们期待着基础教育领域一种全新的教学改革局面的形成!
[1]林崇德.坚持正确政治方向 凝炼学生核心素养[N].北京:中国教育报,2016-9-30.
(本文作者系南开大学教授,博士生导师,《普通高中数学课程标准》修订组核心成员)

