变深度发射性能可靠性影响因素多元逐步回归分析

胡松伟

(91550部队， 辽宁 大连 116023)



变深度发射性能可靠性影响因素多元逐步回归分析

胡松伟

(91550部队， 辽宁 大连 116023)

针对某发射系统变深度性能可靠性影响因素最佳子集获取问题，综合考虑设计偏差、装药性能偏差和环境因素，建立诸因素影响程度的多元逐步回归模型。以性能试验信息为基础，对试验数据中诸影响因素进行相关性分析，计算给出诸影响因素的相关系数，回归分析结果与试验测量结果相吻合；以此为基础进一步获取环境因子进行性能折算，结果表明经多元回归分析修正后的性能参数的估计误差标准差缩小，可有效提高变深度发射性能可靠性的估值精度。

兵器科学与技术； 变深度发射； 性能可靠性； 影响因素； 多元逐步回归分析

0 引言

随着水下发射技术的发展，变深度发射性能可靠性作为评价潜射导弹武器系统的关键战术技术指标，其指标控制偏差不断缩小，评估要求不断提高，基于环境因子仿真进行性能折算的传统评估方法[1]需进一步完善。随着对性能参数分布特性认识的深入，需要进一步采用回归的方法对潜射内弹道性能的环境因子作综合统计分析，以获取影响因素的最佳子集，进一步提高变深度发射能力评估的置信水平。本文针对变深度发射性能可靠性这一概率的影响因素，建立了回归模型，通过比较回归系数来反映与该系数对应因素的贡献大小，以实际发射试验数据为基础，建立相关影响因素与性能参数之间的统计关系，分析了诸影响因素的影响程度，能有效提高变深度性能可靠性的估值精度。

试验检验作为最重要的评估手段，速度、加速度、温度、压强等试验观测量，是评估潜射导弹变深度发射性能可靠性的主要数据，常用的工程分析方法主要有作图比较法、特征值统计法、数学模型法等[2]。前两种方法比较直观，但无法对诸影响因素的效应进行定量分析，数学模型法以试验数据为基础，通过建立回归模型，定量描述性能参数与诸影响因素之间的函数关系，模型经过检验之后，可以反推诸影响因素对性能可靠性的影响程度。但是由于问题十分复杂，很难描述待估性能参数与诸影响因素之间的函数关系。于是可以采用多项式、阶梯函数、样条函数、分段折线等线性化方法进行多元逐步回归[3-6]。但是利用简单曲线也仅能描述单影响因素的主效应，对于多影响因素间的交互效应则需通过三维曲面等高线云图来描述。

1 逐步回归分析原理和算法

1.1 逐步回归分析的原理

逐步回归是一种筛选因素的方法，大多数统计软件均具有逐步回归功能。该方法在考虑的全部因素中按其对性能的作用大小、显著程度大小，由大到小地逐个引入回归方程，而对性能影响不显著的因素始终不被引入回归方程。另外，己被引入回归方程的因素在引入新因素后也可能失去重要性，需要从回归方程中剔除；引入一个因素或者从回归方程中剔除一个因素都称为逐步回归的一步，每一步都要进行分布检验，以保证在引入新因素前回归方程中只含有对性能影响显著的因素，而不显著的因素已被剔除。经过逐步筛选回归，最后用所选上的影响因素子集建立性能参数的回归方程[7-8]。

1.2 回归准则的选择和制定

回归准则就是通常所说的回归模型优劣评价指标，有的统计软件中称之为可决系数。常用的评价指标有：修正复相关系数R2最大法、平均残差平方和(MSE)最小法、马洛斯CP统计量最小法、预测偏差的方差(PBV)最小法、平均预测均方差(APMV)最小法、预测残差平方和(PRESS)最小法、Akaike信息量(AIC)最小法。修正复相关系数R2达到最大，表明性能参数与各影响因素之间的线性相关程度最大，越大模型的拟合优度越高；MSE达到最小，即用连续曲线拟合离散的影响因素的残差平方和最小，表明回归模型的随机误差最小；马洛斯CP统计量达到最小，表明多个候选回归模型的预测精确度接近最佳预测精度，最终得到的回归系数与真实回归系数之间无偏倚；AIC达到最小，表明所估回归模型的复杂度可控、拟合数据最优；PBV达到最小，预测值与真实值之间的差距、预测值的离散程度最小；APMV达到最小，表明预测风险最低、回归模型稳定度最高；PRESS达到最小，表明所得到的回归模型预测残差累积最小，越小表明预测精度越高。

表1 性能参数的试验测量值及回归偏差Tab.1 Live firing performance test data and regression errors

表2 4影响因素的回归子集Tab.2 Regression subsets of influencing factors

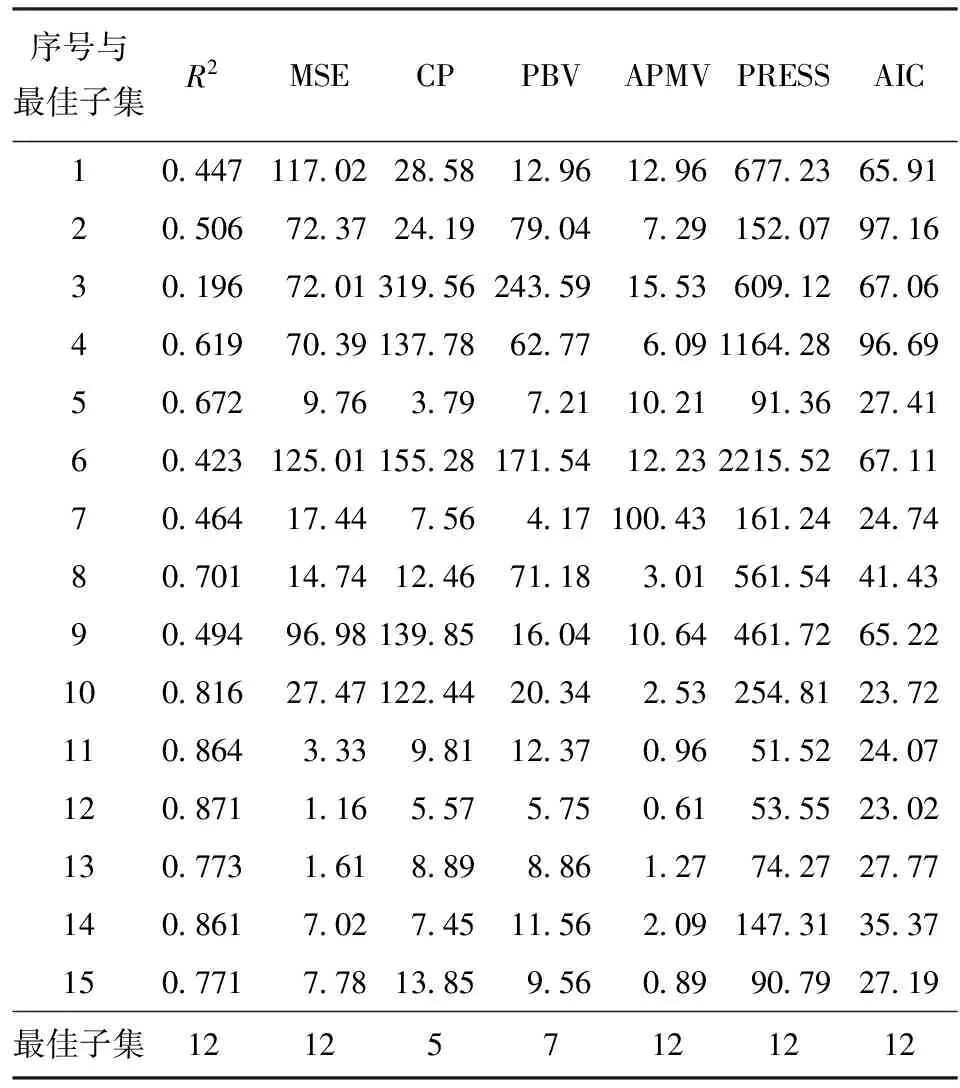
表3 回归子集的7种准则值Tab.3 7 criteria values of regression subsets

由表3可见，不同准则对应的最佳回归子集不同，如果取编号为5的回归子集作为最佳回归子集，就意味着喷水量和发射深度对出筒速度没有影响，这显然不正确；如果取编号为12的回归子集作为最佳回归子集，就意味着发射深度对出筒速度没有影响，这显然也不正确。不难发现利用上述7准则无法确定最佳子集，编号为15的理想回归子集没有被选中，需要寻找新的准则。

为严格满足潜射内弹道性能影响因素回归分析的基本要求，本文将偏回归平方和(PRSS)理论运用到潜射内弹道性能影响因素分析过程中，制定了增加因素和剃除因素的判别准则，即采用标准化影响因素的PRSS极值分析法筛选潜射内弹道性能的影响因素。进行检验时需要用到同时求线性方程组的解以及系数矩阵的逆矩阵的紧凑变换，推导出一系列回归递推公式，包括紧凑变换、回归系数等的递推公式，并根据多元逐步回归分析，以环境因素的相关系数表示并得出诸影响因素的重要程度，这样对性能指标参数与诸因素之间的关系就有了可量化且更直观的认识。

1.3 多元回归方程的建立

假定从总计p个备选影响因素中选取k个影响因素，则可能的线性回归方程共有2k-1个，只有选择最优的影响因素子集建立回归方程，才能获得高精度的环境因子，正确进行性能可靠性的折算与评估。

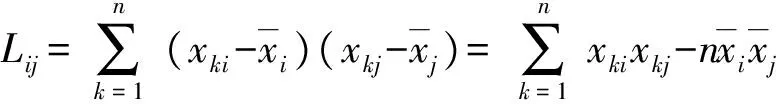
(1)

(2)

i,j=1,2,…,p.

标准化后，几何平均值均为0，标准差为1，则回归方程可以表示为

式中：β0～βp为标准化回归系数；εvj为误差。

若假定εvj独立同分布，其均值为0，方差σ2未知，可以得到其系数矩阵的估计值：

(3)

1.4 回归算法

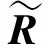
(4)

简化起见，先选定4项影响因素(即取k=4)开始筛选：主装药出厂燃速值用符号u0表示、主装药贮存天数用符号t表示、发射深度用符号H表示、喷水孔数用符号np表示，性能参数以速度参数v为例进行描述。

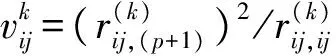
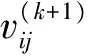
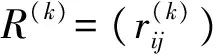
(5)

通过待定系数法可得到回归系数：

(6)

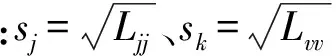
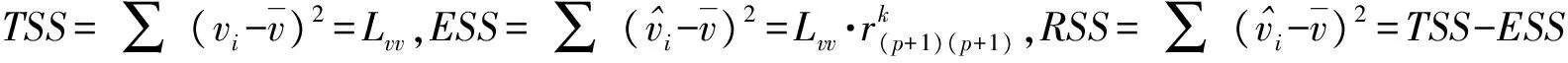
2 试验数据的相关性分析

2.1 性能参数与影响因素的相关性

变深度发射性能可靠性试验共计获取了13组数据，对这13组数据进行相关性分析，若相关系数|rij|≥0.8，则认为因素xi和性能参数v有强的相关性；若0.3≤|rij|<0.8，则认为有弱的相关性；若|rij|<0.3，则认为没有相关性。实际分析表明，诸因素不但独自起作用，而且联合起来起作用，也就是说，不仅诸因素的水平改变时对性能指标有影响，而且诸因素联合搭配对性能指标也有影响。单因素对性能指标的影响通过曲线就可以描述；多因素的联合搭配影响则需通过三维曲面等高线云图来描述，其3个坐标轴分别2个因素和性能指标，描述u0-t-H-np4个影响因素需要6幅云图(见图1～图6)。

图1 u0-t-v三维云图Fig.1 u0-t-v 3D contour map

图2 u0-np-v三维云图Fig.2 u0-np-v 3D contour map

图3 u0-H-v三维云图Fig.3 u0-H-v 3D contour map

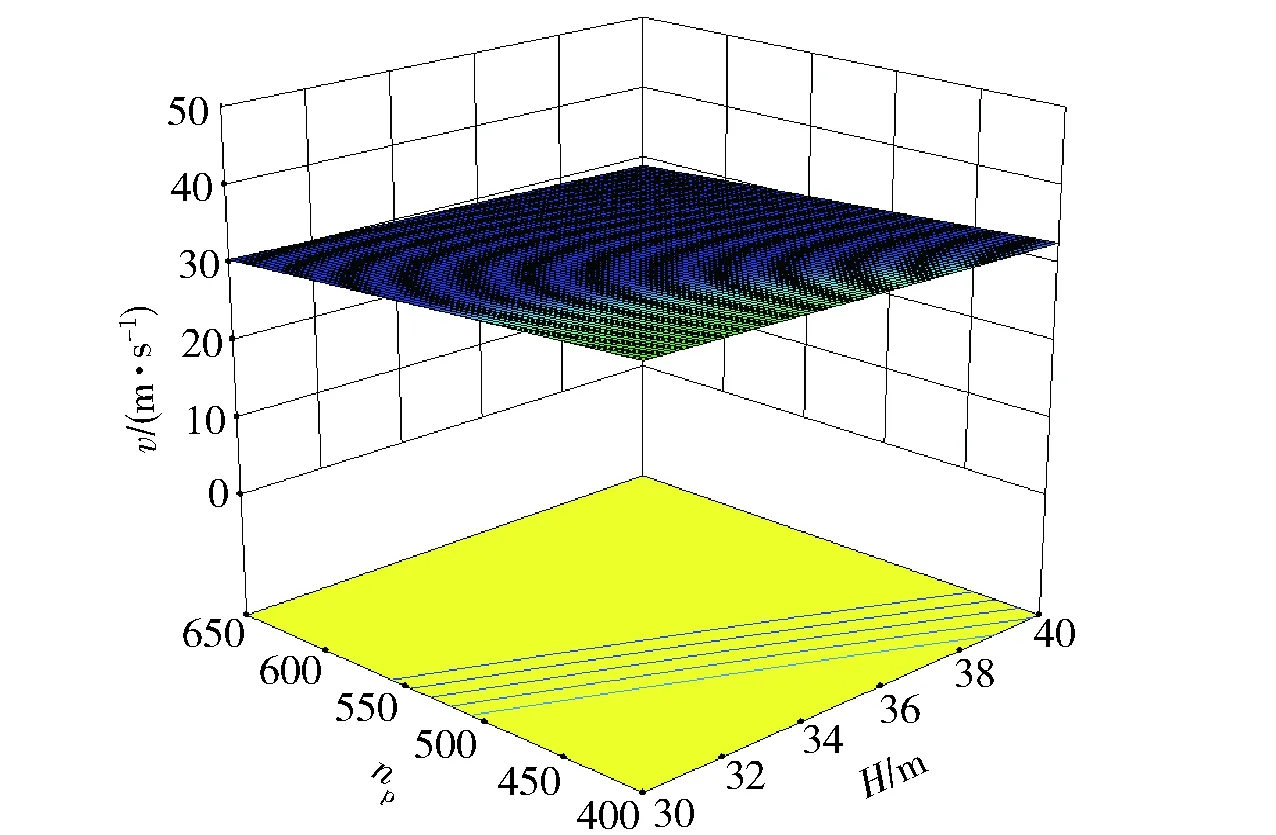
图4 H-np-v三维云图Fig.4 H-np-v 3D contour map

图6 np-t-v三维云图Fig.6 np-t-v 3D contour map

2.2 影响因素之间的相关性检验

采用后退法计算诸影响因素之间的相关系数和相关性显著水平，若诸影响因素之间相关系数较小，且相关性显著水平大于0.05，则可以认为诸影响因素之间是相互独立的，可以采用逐步回归方法求解该多元回归模型的表达式；否则说明影响因素之间的交互作用对性能参数贡献显著，还有必要进行2次回归分析，即需要考虑贡献显著的2次项和交叉项。分析2.1节得到的因素响应曲面云图，图1中性能参数v的截距变化较大，表明因素u0和因素t的组合作用对性能参数v影响较大，回归模型应该考虑该2次交叉项。

3 影响因素的逐步回归分析

3.1 诸影响因素的引入

一般认为，回归方程包含的因素越多，回归平方和越大，剩余平方和越小，剩余均方差也随之愈小，预测值的误差也愈小，模拟的效果愈好。但是如果方程中的因素增多，预报工作量就会加大，其中有些相关性不显著的因素反而会影响预测效果。综合考虑设计偏差、装药性能偏差和环境因素都会影响到发射内弹道性能，进而影响对变深度发射性能可靠性的估计。设计偏差因素包括：喷水压差系数λ、喷水孔数目np、冷却水量Ml、起飞质量M、初始容积当量长度l、弹尾气密环摩擦系数f、导弹适配器摩擦系数z、总压恢复系数μ、流量系数σf；装药性能偏差因素包括：主装药出厂燃速u0、有效装药量m0、装药贮存时间t；环境参数因素包括：发射深度H、装药初温Tt、冷却水初温Tl、筒底空气初温Ta.

贮存试验表明，燃速为29～31 mm/s的装药，在生产后贮存的前3年内燃速会下降约1 mm/s，因此确立装药出厂燃速和装药贮存时间两个相互独立的影响因素，在回归模型中引入2次项u0t项。u0-t-v的等高线云图(见图7)可以直观解释发射时的装药燃速性能u变化对性能参数v的影响。这样分析与依据经验公式u=(u0-0.140 87lnt)·[1+αT(Tt-T20 ℃)](αT为温度敏感系数)得到的预测结果一致(见图8)。

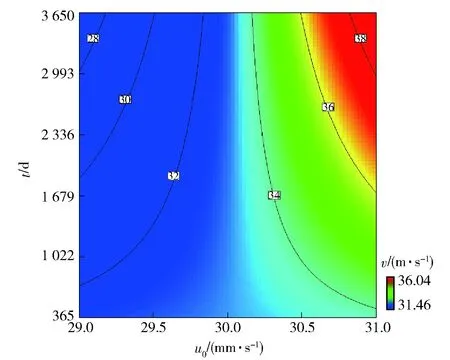
图7 u0-t-v等高线云图Fig.7 u0-t-v contour map

图8 u-t曲线Fig.8 u-t curve

简单的线性回归模型无法解释本文所讨论的问题，只能基于试验数据进行模拟、建模，通过比对线性拟合、2次拟合、3次拟合效果，最终选择拟合最好的模型；同时要尽量免造成过拟合、欠拟合或者由于影响因素间的多重共线性而掩盖某些因素的作用；对于模型的细节，比如要保留哪些模型项，还得依据工程经验予以确定，本文依据模型的方差分析结果来确定哪些因素是重要的，必须在模型中保留。

一旦确定一个因素xk需要引进回归方程，必须利用引进后已经变换的相关系数矩阵，按前面相同的方法对回归方程中已存在的其他因素再逐一进行显著性检验，以确定由于因素xk的引进是否需要将其他因素从回归方程中保留或剔除。具体选择时应注意某些因素高低水平的差值不能过大，以防掩盖了其他因素的重要性，本文最终选取16项可信度大于85%的因素作为重要因素，经过多元回归分析修正后的性能参数的估计误差标准差明显缩小，可有效地提高发射性能可靠性的估值精度。

3.2 逐步回归迭代计算

依据方法步骤建立相关系数矩阵，并进行紧凑变换如下：

…

分别计算各因素的PRSS，并进行显著性检验结果列入表4.

表4 PRSS计算列表Tab.4 Results of PRSS

显著性检验结果表明，4个影响因素对速度贡献较大，此时可建立回归方程：

0.004 336 4t-0.003 917 12np-0.000 032 415u0t.

简化起见，该回归方程省略了较小项，在对第6组性能试验结果2次回归时，出现最大预测偏差σmax=-4.87%(见表1)，还需进一步引入其他影响因素m0、Tt、λ、Ml、Tl、Ta、M、l、f、z、μ、σf项逐步进行回归迭代。

3.3 模型多重共线性诊断处置

回归模型中的冗余信息不但不能提高对性能参数的解释能力，反而会造成过拟合，诸因素间的多重共线性是不容忽视的。如果不消除模型的多重共线性，估计误差标准差等指标就不会得到优化，有时甚至会劣化，因此需要进行回归模型的多重共线性诊断。成熟的解决方法有很多，如岭回归(RR)、主成份回归(PCR)、偏最小二乘回归(PLSR)、约束回归(CR)、压缩估计(SE)、特征根估计(LRE)以及分组压缩主成份估计、岭型压缩主成份估计、组合主成份估计、岭型组合主成份估计等衍生方法。

通常认为RR比偏最小二乘回归要好，但是其岭参数没有明确含义，它的参数估计始终是有偏估计，要谨慎选择变量；PCR具有降维作用，但其回归计算结果仍然会受到重叠信息的影响，并且难以有效确定衡量指标；逐步回归是一种选择变量的建模方法，遇到严重共线性时则舍弃该变量，如果在所有影响因素中寻找到最优子集，那么也就解决了有害共线性问题，所以得到的回归模型还是可以接受的，难点在于F检验显著性水平α选择。分别将RR、PCR和逐步回归得到的回归系数列入表5，可见3种方法得到的结果基本一致，表中RR参数为0.36，PCR方程数为16.

表5 模型项回归系数Tab.5 Regression coefficients of model terms

3.4 回归模型的方差分析

一般认为模型越显著，其可靠性和准确性就越高。对所建回归模型进行显著性检验，进入方程的一次项的P值(在数理统计中表示拒绝假设的概率，在此处也就是回归模型中不能引入该因素对性能参数进行解释的概率)均小于0.000 1，表明利用该回归模型得到的计算结果仅有0.01%的概率不能用该因素解释，并可省略P值大于0.05的2次项和交叉项。

3.5 回归拟合效果

图形化表示便于直观理解回归拟合效果，前文利用三维曲面等高线云图描述了诸因素对性能参数的影响，对回归方程解空间的形状也可以用立方图进行描述(见图9)。

图9 回归方程的解空间Fig.9 Cube plot of sloution space

利用试验数据进行验证，在回归模型的解空间内的估计值与大部分水平组合的试验值相对误差在5%～6%之间，模型预测与试验真值具有较好的吻合度(见图10)，可用于预测不同设计状态和使用工况条件下的出筒速度。

图10 v实测值与预测值的比对Fig.10 Trial result vs. predicted result of v

4 结论

依据工程实践经验，从回归准则的选取、回归算法建模、环境因素筛选、相关性检验、多重共线性诊断处置以及回归模型的方差分析等方面，对影响变深度发射性能可靠性的主要影响因素进行了系统的分析研究。

综合考虑设计偏差、装药性能偏差和环境因素，建立了回归分析模型，回归分析结果与试验测量结果相吻合，能够显著提高变深度发射性能可靠性的估值精度，后续将进一步计算回归模型残差的正态分布概率，获取残差分布特性，进一步优化回归模型，以提高模型的解释能力。

另外，由于诸因素的变化梯度不同，得到的回归系数不尽相同，本文回归方程的回归系数是以表1中各因素的均值为中值，以半标准差为梯度得到的，如果采用该方程进行预测计算，还需详细划分装药燃速、水深和冷却水量等因素水平，才能获得更加精确的解空间。

References)

[1] 胡松伟. 潜射内弹道性能折算与评估方法[J].兵工学报, 2015, 36(9): 1647-1653. HU Song-wei. Converting and evaluation method for submarine launched interior ballistic functional[J]. Acta Armamentarii, 2015, 36(9): 1647-1653.(in Chinese)

[2] 方开泰, 刘民干, 周永道．试验设计与建模[M]．北京:高等教育出版社, 2011. FANG Kai-tai, LIU Min-gan, ZHOU Yong-dao. Design and modeling of experiments[M]. Beijing:Higher Education Press, 2011.(in Chinese)

[3] 李乃宏, 吴瑶华. 多重共线性诊断及其在飞行器非线性气动

模型结构确定和参数估计中的应用[J]. 宇航学报, 2000, 21(3): 24-28. LI Nai-hong, WU Yao-hua. Multicolinearity diagnosis and its application to the determinaton and parameter estimation of nonlinear aerodynamic model[J]. Journal of Astronautics, 2000, 21(3): 24-28. (in Chinese)

[4] 刘庆明, 刘丽斌, 汪建平, 等. 烟酸粉尘云爆炸极限的逻辑回归分析[J]. 兵工学报, 2015, 36(3): 523-529. LIU Qing-ming, LIU Li-bin, WANG Jian-ping, et al. Logistic regression analysis of the explosion limit of nicotinic acid dust cloud[J]. Acta Armamentarii, 2015, 36(3): 523-529.(in Chinese)

[5] 卢家莉, 李彬华, 胡泊. 一种电子倍增CCD电子倍增增益的确定方法[J]. 兵工学报, 2015, 36(4): 710-715. LU Jia-li, LI Bin-hua, HU Po. A method of determining EMCCD electron multiplication gain[J]. Acta Armamentarii, 2015, 36(4): 710-715.(in Chinese)

[6] 陈亮, 刘荣忠, 郭锐, 等. 扭曲尾翼弹箭气动外形多目标优化[J].兵工学报, 2016, 37(7): 1187-1193. CHEN Liang, LIU Rong-zhong, GUO Rui, et al. Multi-objective optimization on aerodynamic shape of projectile with twisted empennages[J]. Acta Armamentarii, 2016, 37(7): 1187-1193. (in Chinese)

[7] 何晓群, 闵素芹, 方开泰. 实用回归分析[M]. 北京:高等教育出版社, 2014. HE Xiao-qun, MIN Su-qin, FANG Kai-tai. Practical regression analysis[M]. Beijing:Higher Education Press, 2014.(in Chinese)

[8] 道格拉斯C.蒙哥马利, 伊丽莎白A.派克, G.杰弗里·瓦伊宁. 线性回归分析导论[M]. 王辰勇, 译. 北京:机械工业出版社, 2016. Montgomery D C, Peck E A, Vining G G. Introduction to linear regression analysis[M]. WANG Chen-yong, translated. Beijing: China Machine Press, 2016. (in Chinese)

[9] 曹宁, 王晓锋, 徐亚栋, 等. 车载炮射击密集度逐步回归分析[J]. 弹道学报, 2012, 24(12): 47-53. CAO Ning, WANG Xiao-feng, XU Ya-dong, et al. Evaluation on firing dispersion of wheeled artillery based on stepwise regression analysis[J]. Journa1 of Ballistics, 2012, 24(12): 47-53. (in Chinese)

Analysis of Influencing Factors on Reliability of Varable DepthSubmarine-launched System Based on Multivariate Stepwise Regression

HU Song-wei

(Unit 91550 of PLA, Dalian 116023, Liaoning, China)

Reliability of underwater varable depth launching system is affected by various influencing factors. The weight and offsetting of projectile are studied by multivariate stepwise regression analysis method, and the second-order algorithm of the models is established. Design deviation, charge performance deviation and environmental factos are taken into account. The relativity analysis for each factor is carried out based on the live firing performance test information of a certain type submarine-launched missile. The effects of the influencing factors, correlation coefficients of each factor and best regression subset are discussed. The results of the regression analysis accords well with the live firing phenomena. Based on this method, the experimental results indicate that the estamated error standard deviation of functional reliability parameter is improved. Multiple stepwise regression method improves the estimation precision. It is feasible and effective to analyze the influencing factors.

ordnance science and technology; changeble-depth launch; performance reliability; influencing factor; multiple stepwise regression analysis

2016-08-24

军内科研项目(2013年)

胡松伟(1976—), 男, 工程师。 E-mail: goto55@sina.com

TJ762.4+1

A

1000-1093(2017)05-0986-09

10.3969/j.issn.1000-1093.2017.05.019