多轮独立电驱动车辆转向稳定性集成控制研究

廖自力， 阳贵兵， 高强， 袁东

(装甲兵工程学院 控制工程系， 北京 100072)



多轮独立电驱动车辆转向稳定性集成控制研究

廖自力， 阳贵兵， 高强， 袁东

(装甲兵工程学院 控制工程系， 北京 100072)

为提高多轮独立电驱动车辆转向稳定性，提出一种以直接横摆力矩控制为核心的集成控制方法，分别设计直接横摆力矩上层目标跟踪控制器和下层转矩协调控制器，并对下层控制器进行多层次优化设计。采用转矩预分配、最优滑转率控制分配和补偿分配相结合的多层次分配结构，实现系统层面和单个驱动轮转矩的优化分配控制，最大限度减小横摆力矩执行误差。基于某型8轮独立电驱动试验样车，进行低附着路面和良好路面双移线行驶试验。试验结果表明：设计的集成控制器有效提高了车辆转向的稳定性，能实现对期望转向轨迹的良好跟踪。

控制科学与技术； 多轮独立电驱动； 直接横摆力矩控制； 最优滑转率； 集成控制

0 引言

直接横摆力矩控制(DYC)是目前应用比较广泛的车辆操纵稳定性控制技术[1-3]。相比于机械传动车辆依赖制动系统实施横摆力矩控制，采用轮毂电机驱动的车辆可依靠独立性和控制精度更高的电机系统实现，由于驱动电机响应速度快、控制精度高以及可以迅速在驱动/制动状态间切换等优势[3]，为多轮独立电驱动车辆的DYC提供了更有利的硬件基础。

目前，DYC大多采用分层控制结构：上层为运动跟踪控制，下层为转矩协调控制[4]。多轮独立电驱动车辆在下层转矩分配控制中，可抛开传统针对制动系统设计的基于规则的转矩分配方式，而采用更加灵活的分配算法。现有的研究中，比较常见的分配算法有：基于电动机消耗能量最小的广义逆算法[5]、基于轮胎利用率最小的二次规划算法[6]等。然而这些分配算法并未考虑车轮之间附着差异带来的影响，算法在实际运用中有一定限制。

多轮独立驱动车辆由于驱动轮较多，轮间附着差异较大，如何充分利用每个驱动轮的地面附着力，最大限度发挥车辆转向性能，显然从广义层面无法解决，而进行单轮的最优滑转率控制(驱动防滑控制)是最有效的解决方法。现有的最优滑转率控制一般是在底层的电机控制系统里面实现[7]，这样控制存在的问题是被削弱的转矩无法在其他驱动电机上得到补偿，增加了横摆力矩的执行误差。

1 转向稳定性集成控制器结构

本文提出的8轮独立电驱动轮式车辆转向稳定性集成控制器结构如图1所示。

图1 转向稳定性集成控制器结构Fig.1 Structure of steering stability integrated controller

图1中，控制系统分为上、下两层结构，上层为目标跟踪控制，下层为转矩协调控制，上层控制器的输入为驾驶员操作信息和反馈的车辆状态信息，下层控制器输出的转矩直接作用于车辆系统。

2 上层控制器设计

2.1 车辆参考模型

在车辆稳定性分析中，以侧向和横摆运动这2个自由度为对象的线性2自由度模型应用最为广泛，其原因：1)这2个自由度反映了车辆稳定性中最重要的动力学特性；2)线性区域是车辆运动的理想区域[8]。本文研究的车辆为双前桥转向的4轴车辆，其单轨2自由度模型如图2所示。

图2 4轴车辆单轨2自由度模型Fig.2 Monorail 2-DOF model of four-axil vehicle

图2中：v为车速；vx为纵向车速；vy为横向车速；Fxi、Fyi(i=1,2,3,4)分别为第i轴车轮的纵向力和侧向力；αi(i=1,2,3,4)为第i轴车轮的侧偏角；δ1、δ2分别为前两轴车轮的转向角；Li(i=1,2,3,4)为第i轴距离车辆质心处的距离。

只考虑车辆的侧向运动和横摆运动，不考虑纵向力的影响，根据牛顿第二定律，侧向加速度与侧向力满足

(1)

式中：m为车辆质量。

根据欧拉第二定律，横摆角加速度与横摆力矩满足

Fy3L3+Fy4L4+M，

(2)

式中：Ir为车身转动惯量；M计算方式为

(3)

l为轮距，ΔFxi为两侧纵向驱动力差值。

(4)

(5)

在轮胎侧偏特性线性化的假设条件下，轮胎侧向力与侧偏角呈比例关系，即

Fyi=Cαiαi，

(6)

式中：Cαi(i=1,2,3,4)为第i轴的侧偏刚度，为左、右侧轮胎侧偏刚度之和，即Cαi=Cαil+Cαir.

各轮侧偏角关系为

(7)

将(6)式、(7)式代入(4)式、(5)式中，得到4轴双前桥转向车辆线性2自由度模型的状态空间表达式：

(8)

计算参考横摆角速度时，以零化质心侧偏角模型为基础进行计算，并采用滑模控制算法计算期望的摆力矩M，具体计算方法参考文献[9]。

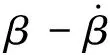
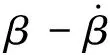
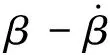
图3 不同路面附着系数μ、车速v和前轮转角δ 影响下的相平面轨迹Fig.3 phase plane influenced by road adhesion coefficient μ, speed v and front wheel angle δ

假设μ、v和δ3个因素的影响相互独立，综合考虑3个影响因素，并且忽略前轮转角对边界线斜率的影响，只考虑其对焦点平移的影响，则相平面稳定区域可表示为

(9)

式中：1/B1=p1v+p2为边界线的斜率，B2=f(μ)·(1+p3δ)，B3=-f(μ)(1-p3δ)，p1、p2、p3可通过数据拟合得到，f(μ)为路面附着系数μ影响下的质心侧偏角极限值，可将其近似计算为

f(μ)=βmax=arctan(0.02μg)，

(10)

g为重力加速度。

图4 控制区域划分Fig.4 Control area

3 下层控制器设计

采用多层优化结构设计下层控制器对转矩进行协调控制，多层优化结构中包含了预分配控制、基于最优滑转率控制以及再分配冗余控制。通过预分配控制保证系统层面的需求横摆力矩，通过最优滑转率控制以及再分配冗余控制保证驱动轮的最优转矩输出，从而最大限度减小横摆力矩的执行误差。

3.1 预分配控制

正常情况下，横摆力矩的分配要满足两方面的需求：整车纵向驱动力和转向横摆力矩，也就说，当车辆运行在线性区域时，各驱动轮力矩的分配尽量不影响整车的纵向驱动力需求，不降低过弯车速；当车辆运行与非线性区域，则要以牺牲纵向驱动力，来满足稳定转向的横摆力矩要求。

基于以上分析，本文将8个驱动电机分为4组：左前Tlf、左后Tlr、右前Trf、右后Trr，分配算法如下(以向左转为例)：

(11)

式中：B为轮距；Td为驱动踏板对应的总力矩需求；ΔMi、ΔMo分别施加在内侧后两轴与外侧前两轴的附加力矩，

(12)

(13)

Δβ=β-βref，Kp、Ki、Kd为PID控制器的比例、积分与微分系数，dM/dβ≥0表示不足转向，dM/dβ≤0表示过转向，即不足转向时，在内侧后两轴施加基于质心侧偏角控制的制动力，过转向时，在外侧前两轴施加制动力。

3.2 最优滑转率控制+补偿控制

采用基于最优滑转率滑模控制方法对电机输出转矩进行控制，其中，车轮最优滑转率的识别方法在文献[11]有介绍。

车辆在水平路面时的车轮模型为

(14)

式中：J为车轮转动惯量；ω为车轮的角速度；i为传动比；Td为电机实际输出转矩值；F(t)为轮胎所收的地面附着力和滚动阻力之和。

驱动电机简化为1阶动态系统模型：

(15)

式中：Tref为电机转矩参考值；τ为电机相应时间常数。

令x1=ω，x2=Td，建立系统状态方程：

(16)

选取两个线性滑模面：

(17)

式中：x1d、x2d分别为最优滑转率点所对应的电机转速的期望值和实际输出转矩的期望值。

选择指数趋近率：

(18)

式中：k1>0，q1>0，k2>0，q2>0.k1、k2的值决定了趋近的速度，其值越大，趋近的速度越快，但是可能导致到达滑模面后出现比较大的抖振；通过调节q1、q2的值可有效保证非滑模运动具有良好品质。因此，在参数选择时，可适当增大q1、q2的值，减小k1、k2的值。

将(17)式代入(18)式得

(19)

联立(16)式得

联立(14)式和(15)式，消除x2，得

Tref=

(20)

Tref即为最优滑转率控制输出的转矩值，对每个驱动轮单独进行控制，因此需计算8次，得到8个优化转矩值Tref1，…，Tref8.

对最优滑转率控制分配后，增加转矩补偿控制，将打滑车轮减小的转矩补偿到其他驱动轮上。以左侧车轮为例，首先判断驱动轮是否打滑，车轮滑转情况可根据车速与车轮转速进行计算，滑转率表达式为

(21)

式中：r表示车轮半径。当滑转率λ超出最优滑转率值，则可判定该车轮发生了打滑，并计算目标驱动轮因防滑控制而损失的转矩ΔT.

其次，对该侧电机进行基于补偿控制的转矩再分配：

(22)

式中：εi=1表示第i个车轮有滑转，εi=0表示该车轮正常；N表示未打滑的车轮数量。

4 试验验证

试验样车为某型8轮轮毂电机驱动轮式装甲车辆，车辆的总体质量、电机最大转矩以及主要的驾驶员输入信号参数见表1. 轮毂电机及其逆变器如图5和图6所示。进行低附着路面双移线与良好路面双移线两种试验工况，试验数据由显控终端(见图7)显示和存储，试验过程中车辆的运行轨迹根据轮胎痕迹辨识(见图8)。

表1 主要参数信息Tab.1 Main parameters

图5 轮毂电机Fig.5 In-wheel motor

图6 电机逆变器Fig.6 Motor converter

图7 显控终端Fig.7 Display-control equipment

图8 车辆转向行驶轨迹Fig.8 Moving trajectory of vehicle

采用对比试验，有控制表示采用本文的转向控制策略控制，无控制表示8个驱动电机平均分配扭矩。

4.1 低附着路面双移线行驶

路面附着系数μ=0.3，目标车速为40 km/h，进行双移线仿真试验，期望路径和车辆状态响应如图9所示，转矩信息如图10所示。

图9 车辆状态响应Fig.9 Vehicle state response

图10 转矩响应Fig.10 Torque response

由图9(a)可知，无控制的车辆方向盘转角输入比有控制的车辆大，且有超调；由图9(b)可知，有控制车辆车速基本能稳定在40 km/h左右，而无控制的车辆车速有明显的降低；由图9(c)～图9(f)可以看出，有控制的车辆横摆角速度偏差明显比无控制的车轮小，且质心侧偏角在稳定区域范围内，而无控制的车辆质心侧偏角超出了稳定边界，车辆出现失稳现象，无法跟随期望的路径；图9(g)和图9(h)对比可知，防滑控制器对车轮的打滑情况控制明显，车轮滑转率明显小于无控制车辆，且基本稳定在最优滑转率范围内。对比试验可知，有控制的车辆，车辆的状态信息更稳定。

无控制的车辆按照图10(a)油门踏板给定的转矩值等量分配给8个驱动电机；由图10(b)可知，下层控制器对转矩的协调控制，实现了轴间以及内外侧电机转矩优化分配，转向时外侧电机转矩明显大于内侧值，且电机的最大转矩由900 N·m(油门踏板给下的最大值)降低到500 N·m左右，避免了车辆在低附着路面启动加速阶段出现的打滑情况；由图10(c)可知，在横摆力矩控制作用下，整车转向的实际横摆力矩基本上能跟踪期望的横摆力矩需求。

4.2 良好路面双移线行驶

路面附着系数μ=0.7，目标车速为70 km/h，进行双移线仿真试验，期望路径和车辆状态响应如图11所示，下层控制器的转矩分配结果如图12所示。

由图11可知，有控制车辆车速基本能稳定在70 km/h左右，而无控制的车辆车速有明显的降低；有控制的车辆方向盘转角、横摆角速度偏差、质心侧偏角以及车轮滑转率都比无控制的车辆小，有控制状态下车辆有更好的轨迹跟踪能量。由对比试验可知，有控制的车辆，车辆的状态信息更稳定。

由图12(a)可知，油门踏板基踩到满程，油门踏板给定的转矩值基本达到电机的外转矩特性，最大转矩1 100 N·m；图12(b)车辆在高附着路面双移线行驶的直线加速阶段，加速过程中由于前两轴载荷较小，为防止前两轴车轮打滑，防滑控制器减小了其电机的转矩给定，同时通过补偿控制将减小量增加后两轴驱动电机上，后两轴电机给定转矩的最大值达到1 200 N·m(1 200 N·m为设定的电机转矩上限值)，车辆进入弯道后，下层控制器对前后轴以及内外侧电机转矩进一步优化控制，得到最优的电机给定转矩值；由图12(c)可知，优化控制后的车辆转向实际横摆力矩基本上能跟踪期望的横摆力矩需求。

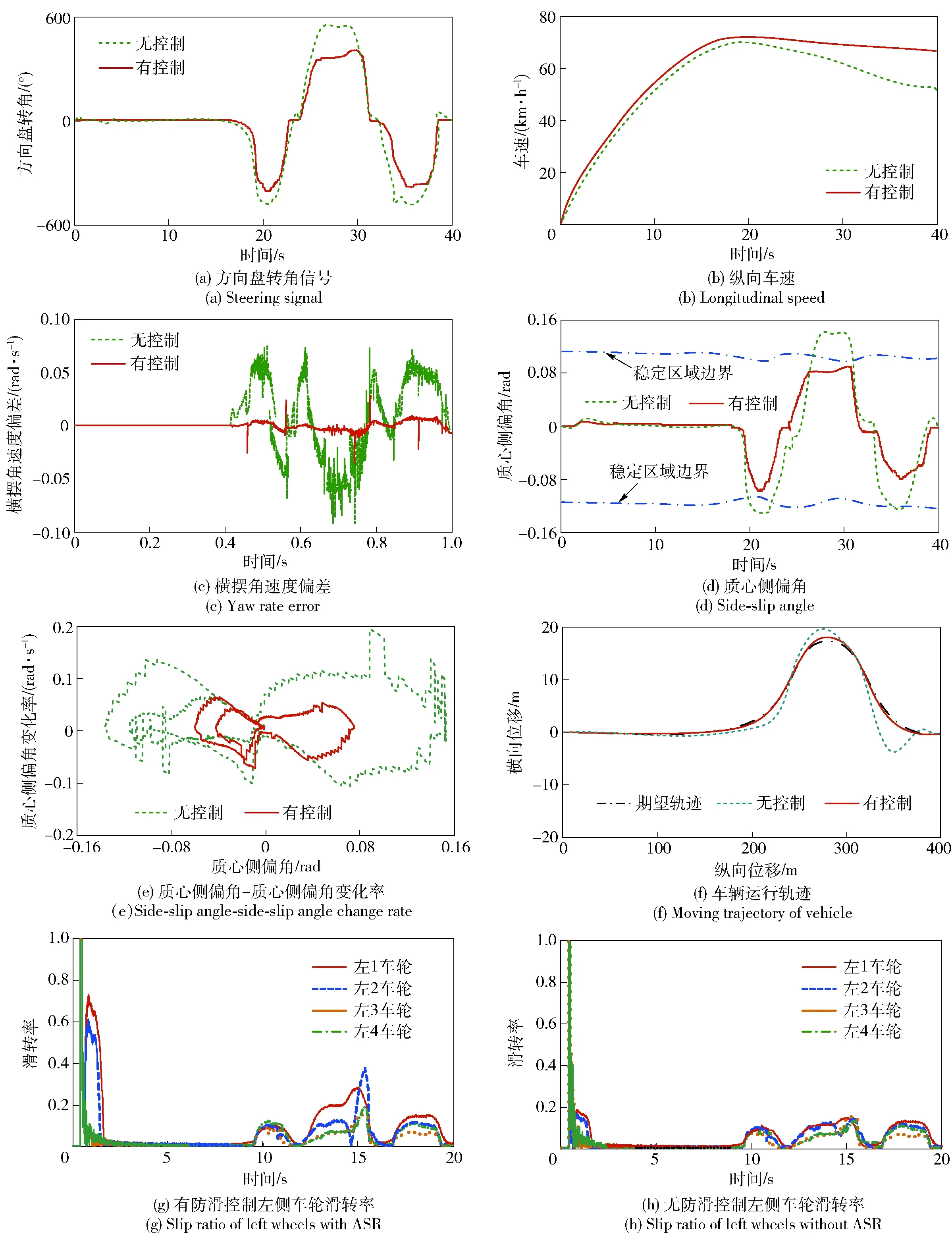
图11 车辆状态响应Fig.11 Vehicle state response

5 结论

本文针对多轮独立电驱动轮式装甲车辆提出了一种基于横摆力矩控制与最优滑转率集成控制的转向稳定性控制策略，并通过样车试验得到以下结论：

1) 通过将最优滑转率控制集成到横摆力矩下层转矩协调分配控制中，解决了传统横摆力矩控制无法实现单轮驱动力最优控制的问题，最大限度减小了横摆力矩的执行误差。

2) 通过实车试验，验证了滑模控制算法具有较好的实时性，适合于具有不确定性外部干扰系统的稳定性控制。

3)采用动力学集成控制，可充分发挥各自控制的优点，实现了各部分功能的集中，且便于实车控制程序的开发，对于可控性和独立性更好、执行机构相对统一的电传动车辆来说，集成控制的方法无疑是其动力学控制研究的重要方向，对于发挥多轮独立电驱动轮式装甲车辆的性能优势，提高其战场生存能力具有重大意义。

图12 转矩响应Fig.12 Torque response

References)

[1] 余卓平, 冯源, 熊璐.分布式驱动电动汽车动力学控制发展现状综述[J]. 机械工程学报, 2013, 49(8):105-114. YU Zhuo-ping, FENG Yuan, XIONG Lu. Review on vehicle dynamics control of distributed drive electric vehicle[J]. Journal of Mechanical Engineering, 2013, 49(8):105-114.(in Chinese)

[2] Nagai M. Perspective of research for enhancing active safety based on advanced control technology[J]. Journal of Automotive Safety and Energy, 2010, 1(1): 14-22.

[3] Kim J, Park C, Hwang S, et al. Control algorithm for an inde-pendent motor-drive vehicle[J]. IEEE Transactions on Vehicular Technology, 2010, 59(7):3213-3222.

[4] 刘维平, 袁磊, 刘西侠. 三轴全轮转向车辆水平集成控制研究[J]. 兵工学报, 2016, 37(2):203-210. LIU Wei-ping, YUAN Lei, LIU Xi-xia. Study of integrated control of all-wheel-steering three-axil vehicle[J]. Acta Armamentarii, 2016, 37(2):203-210.(in Chinese)

[5] Peng H, Hori Y. Optimum traction force distribution for stability improvement of 4WD EV in critical driving condition[C]∥9th IEEE International Workshop on Advanced Control Motion. Istanbul, Turkey: IEEE,2006:596-601.

[6] 邹广才, 罗禹贡, 李克强. 基于全轮纵向力优化分配的4WD车辆直接横摆力矩控制[J]. 农业机械学报,2009, 40(5):1-6. ZOU Guang-cai, LUO Yu-gong, LI Ke-qiang. 4WD vehicle DYC based on tire longitudinal forces optimization distribution[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(5):1-6.(in Chinese)

[7] Tahami F, Kazemi R, Farhanghi S. A novel driver assist stability system for all-wheel-drive electric vehicles[J]. IEEE Transactions on Vehicular Technology, 2003, 52(3):683-692.

[8] Rajamani R. Vehicle dynamics and control [M]. NY, US: Springer, 2006:23-25.

[9] 阳贵兵, 马晓军, 廖自力, 等. 轮毂电机驱动车辆双重转向直接横摆力矩控制[J]. 兵工学报, 2016, 37(2):211-218. YANG Gui-bing, MA Xiao-jun, LIAO Zi-li, et al. Direct yaw moment control in dual-steering for in-wheel motor drive vehicle[J]. Acta Armamentarii, 2016, 37(2):211-218.(in Chinese)

[10] 张晨晨, 夏群生, 何乐. 质心侧偏角对车辆稳定性影响的研[J]. 汽车工程, 2011, 33(4):277-282. ZHANG Chen-chen, XIA Qun-sheng, HE Le. A study on the influence of sideslip angle at mass center on vehicle stability[J]. Automotive Engineering, 2011, 33(4):277-282.(in Chinese)

[11] 阳贵兵, 廖自力, 马晓军, 等. 多轮独立电驱动车辆驱动力优化控制研究[J]. 兵工学报, 2016, 37(1):23-30. YANG Gui-bing, LIAO Zi-li, MA Xiao-jun, et al. A study on driving force optimal control of multi-wheel independent electric drive vehicle[J]. Acta Armamentarii, 2016, 37(1):23-30.(in Chinese)

Research on Integrated Control of Steering Stability of Multi-wheelIndependent Electric Drive Vehicle

LIAO Zi-li， YANG Gui-bing， GAO Qiang， YUAN Dong

(Department of Control Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

An integrated control method based on direct yaw moment control (DYC) is designed to improve the steering stability of multi-wheel independent electric drive vehicle, which includes the upper coordinated controller and the lower controller. The lower controller is optimized by designing a distribution with pre-distribution, driving skid-resistance control and compensation. The optimized torques of the system and the driving wheels keep the performing error of yaw moment minimal. The double lane change experiments of a prototype vehicle on low friction road and high friction road show that the integrated controller can improve the steering stability significantly and follow the desired tracks.

control science and technology; multi-wheel independent electric drive; direct yaw moment control; optimal slip ratio; integrated control

2016-07-27

国家自然科学基金项目(51507190)

廖自力(1974—)， 男， 副教授， 博士生导师。 E-mail: 569024533@qq.com

TJ810.3+23

A

1000-1093(2017)05-0833-10

10.3969/j.issn.1000-1093.2017.05.001