基于跳数量化的无线传感器网络节点定位算法
张石, 张百海, 王飞帆, 关子霄
(北京理工大学 自动化学院, 北京 100081)
基于跳数量化的无线传感器网络节点定位算法
张石, 张百海, 王飞帆, 关子霄
(北京理工大学 自动化学院, 北京 100081)
为提高无线传感器网络节点定位精度,提出一种基于跳数量化的定位(MDS-HE)算法。将网络中节点的一跳邻居节点集合分割成3个不相交的子集,根据跳环分割的相交区域面积来估算节点间的距离,从而将整数跳数转换成实数跳数,转换后节点间实数跳数更能准确地表示节点间的距离;将实数跳数矩阵应用于多维定标(MDS)算法中,并且引入扩展卡尔曼滤波算法对节点坐标进行准确定位。在节点随机布撒的网络中,对提出的算法进行了仿真和实验分析。仿真和实验结果表明:在不同节点数量情况下,MDS-HE算法的性能优于距离向量定位算法和经典MDS算法,而且在锚节点足够多的条件下,MDS-HE算法定位更加准确。
信息处理技术; 无线传感器网络; 定位; 多维定标算法; 跳数量化; 扩展卡尔曼滤波
0 引言
无线传感器网络(WSNs)是由大量的具有感知性能,处理和发送环境信息的传感装置组成。无线传感器网络的发展引起了全世界的广泛关注,它在战场监视、环境监测、生物检测、智能空间、产业诊断等领域得到广泛的应用[1-4]。
节点定位技术是无线传感器网络中一个重要的研究课题[5-7]。节点定位就是准确地确定传感器节点在网络中的坐标。根据是否使用测量节点间的距离,节点定位方法分为基于距离定位方法和距离无关定位方法[8]。基于距离定位方法使用硬件来测量节点间的距离,并利用距离信息计算节点的坐标。距离无关定位方法只使用跳数或者连通性信息来估计距离和定位节点。虽然后者得到的定位精度不高,但是其成本效益已使它们在大规模和资源受限的传感器网络中得到广泛的应用。
近年来,国内外研究学者提出了很多针对传感器网络节点定位的方法。张新平等[9]提出了一种改进的距离向量定位(DV-Hop)算法,该算法对邻居节点进行分类,将节点的通信范围划分不同的区域,通过几何分析计算出节点到锚节点间距离,提高节点定位的精度,但增加了网络计算量,提升了网络的能量损耗。吴光等[10]提出了一种基于归一化邻居距离的定位算法,该算法的实现仅依赖于节点间的连接性和少量的邻居列表交换,无需增加额外测距硬件,但实际应用中需要大量的节点,增加了节点定位成本。夏少波等[11]提出一种基于跳数区域划分的DV-Hop改进算法,该算法优化了参与定位的锚节点组合,采用质心法确定节点坐标,但节点定位误差没有显著提高。Chen等[12]提出一种单跳距校正节点定位算法,该算法使用节点的邻居节点个数估计节点间距离,但该算法在节点密度低的环境下,定位准确率比较低。Han等[13]提出一种基于节点分布定位算法,该算法假设单位区域内节点的个数是相同的,节点通过优化目标函数估计邻居节点位置,通过邻居节点分布估计节点位置,但该算法需要大量测距硬件,增加定位成本。Sarita等[14]提出一种距离无关定位算法,该算法利用跳数估计节点和锚节点间的距离,从而进行节点定位,但该算法只有在节点密度较高情况下定位效果较好。在基于跳数的定位算法中,大都采用整数跳数进行节点定位,由于整数跳数不能准确描述节点间距离信息,所以导致定位效果较差。
为了提高节点定位精度,本文提出了一种基于跳数量化的节点定位(MDS-HE)算法。算法根据节点的一跳邻居节点的分布进一步量化整数跳数,利用跳环分割相交区域面积来估计节点间的距离,将整数跳数转换成实数跳数。对转换后的实数跳数应用多维定标(MDS)算法[15],并且引入扩展卡尔曼滤波(EKF)算法对节点坐标进行准确定位。通过Matlab软件进行仿真和节点定位实验,并与其他定位算法进行性能对比,结果表明,MDS-HE定位算法在定位精度上得到明显提高。
1 系统模型
本文假设节点可以与其通信半径r范围内的所有节点通信,不能与其通信范围之外的节点通信,所有节点和锚节点具有相同的通信范围,并且随机分布在一个相互连通的网络中[16]。设N表示节点的个数,M表示锚节点的个数,它们随机分布在面积为A的任意形状网络中。假设网络区域的面积远远大于节点通信范围面积,即A≥πr2. 这里不考虑边界影响[17],假设所有的锚节点间,节点和锚节点间的跳数h是已知的。
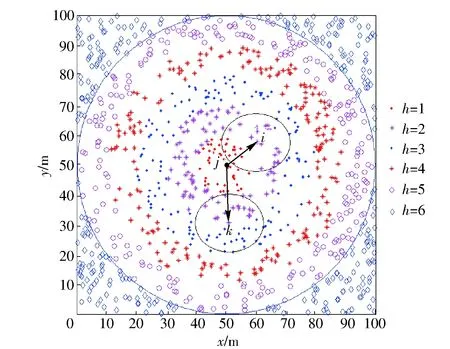
图1 不同跳数的节点分布Fig.1 Node distribution of different hop-counts
图1描绘了一个1 000个节点随机分布在一个100 m×100 m正方形区域,假设锚节点j位于区域中心,相对于锚节点j,不同跳数的节点用不同符号表示。dij和dkj分别表示节点i和k到锚节点j的估计距离。从图1中看出,节点i和k有相同的跳数h=2. 在传统的基于跳数的定位算法中,由于节点i和节点k到锚节点j有相同的跳数,所以dij=dkj. 然而从图1中可以明显看出dij 图2 跳环示意图Fig.2 Illustration of hop rings 图3 理想跳跃模型Fig.3 Perfect hopping scenario 基于邻域划分的跳数量化是通过计算相交区域面积,得到节点到锚节点间的距离,然后将所有整数跳数转变成实数跳数。 2.1 基于跳数和邻居节点分布的节点到锚节点间距离计算 2.1.1 计算相交区域面积 (1) (2) (3) (4) 图4 相交区域面积估算Fig.4 Intersection area estimation (5) (6) (7) 2.1.2 计算节点到锚节点间距离 设di表示节点i到锚节点间距离,3个相交区域真实面积计算方程为 (8) (9) (10) 利用相交区域的估计面积可以计算得到节点到锚节点的距离。设di=f(Ai)表示上述等式中的非线性函数,使用正割法[18]可以得到: (11) (12) 2.2 跳数量化 (13) (14) 无线传感器网络定位算法中最基本的两个步骤是测量几何关系和优化:1)得到节点和锚节点间的几何关系;2)通过几何关系,应用各类优化算法计算节点坐标。基于跳数量化的MDS定位算法将转换后的实数跳数矩阵HR应用到MDS算法中,解决节点定位问题。 3.1 计算相对坐标 多维定标技术的目的就是利用各实体间的相异性来构造多维空间上点的相对坐标图,构造的多维空间上点与各实体相对应,如果两个实体越相似,它们对应于空间上点之间的距离就越接近。其接近程度用胁强系数J来衡量: (15) 式中:f(hij)=ahij+c是跳数的线性标度,a和c是两个常数。应用MDS算法,可以得到节点的相对坐标。 3.2 计算绝对坐标 (16) 通过(17)式可以得到参数向量x: Bx=c, (17) EKF算法的基本思想是将非线性系统线性化,然后进行卡尔曼滤波。它将MDS算法和线性变换定位所得的节点坐标作为初始值,利用节点的所有邻居节点信息进行迭代计算,逐步减小定位误差,提高定位精度。EKF算法过程: 1)建立状态方程 X(k+1)=PX(k)+V(k), (18) (19) 2)建立量测方程,将节点与邻居节点间距离的量测值作为观测量,得到量测方程: z(k)=h(k,X(k))+W(k), (20) 式中:h(·)是一个非线性量测函数;W(k)是节点在k时刻的量测噪声。 假设节点i的初始位置估计为(xi,yi),节点o、p、q是节点i的邻居节点,它们的坐标由MDS算法和线性变换得到,分别为(xo,yo)、(xp,yp)和(xq,yq). 迭代的初始值为 H0= (21) (22) (23) 式中:Δ为预设的容错值,本文取值Δ=0.01;Xk为第k次迭代所得的定位结果;Xk-1为第k-1次迭代所得的定位结果。 (24) 在Matlab环境下对算法进行仿真,并将MDS-HE算法与DV-Hop算法和MDS算法进行比较。 节点个数N从400个增加到1 000个,定位误差仿真结果如图5所示。随着节点数量的增加,3种算法的定位误差随着网络中节点数量的增加均减小,这是因为对于这3种算法,节点数量的增加使得锚节点到节点间估计距离和节点间估计距离更加准确,因此使得定位误差减小。在相同参数情况下,MDS-HE算法的定位精度比DV-Hop算法和MDS算法都要高,这是因为DV-Hop算法和MDS算法仅仅应用整数跳数估计锚节点和节点间的距离和节点间的距离,相对于同一个锚节点具有相同跳数的不同节点,它们与同一个锚节点间的估计距离相同,但是它们实际距离是不同的,因此导致这两种算法定位误差较大。MDS-HE算法将整数跳数转变成实数跳数,实数跳数矩阵得以优化,因此利用实数跳数得到的节点间估计距离更加精确。通过MDS算法,得到的节点的坐标更加精确,并且利用EKF算法对节点位置进行优化,提高了节点的定位精度,减少了定位误差。 图5 不同节点数量下定位误差比较Fig.5 Comparison of localization errors in the case of different number of nodes 节点数量为500个,锚节点数量为5个,整个MDS-HE算法的定位过程如图6~图8所示,节点随机分布如图6所示,通过MDS算法得到节点相对坐标如图7所示,通过线性变换得到节点绝对坐标如图8所示。 图6 节点随机分布Fig.6 Randomly deployed nodes 图7 节点相对坐标Fig.7 Relative coordinates of nodes 图8 节点绝对坐标Fig.8 Absolute coordinates of nodes 节点数量为500个,锚节点数量为5个,最终定位结果如图9所示,绿色星形代表节点真实位置,红色圆圈代表节点估计位置,蓝线代表节点定位误差。可以看出,MDS-HE算法在部分区域定位效果不是十分理想,这是因为锚节点数与节点数比例相对较小,锚节点分布不均匀。节点数量不变,锚节点数量增加到10个,MDS-HE算法最终定位效果如图10所示,节点的定位效果得到显著提高。 图10 10个锚节点MDS-HE算法定位误差效果Fig.10 Localization error of MDS-HE algorithm for M=10 为了进一步验证MDS-HE算法的有效性,采用美国Crossbow公司生产的IRIS-XM2110和MIB520网关进行定位实验。 本次实验在相对空旷的区域进行。针对MDS-HE算法的特性,实验整体设计为:将基站视为未知节点并与笔记本电脑相连,IRIS节点视为锚节点,可以人工部署到区域中;基站收集IRIS节点的信息,并且将信息传输到笔记本电脑中,再利用MDS-HE算法进行计算分析从而实现定位。本次实验的部署区域为20 m×20 m的区域,其中一次的节点部署如图11所示。 图11 节点分布Fig.11 Nodes distribution 6.1 不同定位算法误差对比实验 任意部署5个锚节点位置,分别对3种算法进行10次实验,定位结果如表1所示,表中定位误差为未知节点实际坐标与定位坐标间的距离值。从表1中可以看出,MDS-HE算法的定位误差相对于DV-Hop算法和MDS算法有了一定程度的降低。其中几次实验定位效果与DV-Hop算法和MDS算法差别不大,这是因为锚节点个数较少。 表1 不同算法定位误差比较Tab.1 Comparison of localization errors of different algorithms 6.2 不同锚节点数量MDS-HE定位算法实验 不同锚节点个数的MDS-HE算法的实验结果如表2所示,随着锚节点个数从5个增加到10个,节点间估计距离更加准确。应用MDS算法,得到节点坐标,并引入EKF算法使得节点实际坐标更加准确,定位精度得以提高,实验结果验证了仿真的结论。 表2 不同锚节点数量下MDS-HE算法定位误差Tab.2 Localization errors of MDS-HE algorithm against anchor node number 本文针对节点随机分布的无线传感器网络提出了一种MDS-HE定位算法。该算法利用节点1跳邻居节点分布,将整数跳数转换成实数跳数,构造实数跳数矩阵,应用MDS算法,并且引入EKF算法对节点坐标准确定位,并分别研究了该算法在仿真环境下和实际应用中的定位效果。 仿真结果表明:在节点个数相同条件下,MDS-HE算法的定位误差明显低于DV-Hop算法和MDS算法;随着锚节点个数的增加,MDS-HE算法的定位精度提高。 实验结果表明,在锚节点个数相对较多的情况下,MDS-HE算法表现出的定位精度更高。 References) [1] 朱明强, 侯建军, 刘颖, 等. 基于自适应比例修正无迹卡尔曼滤波的目标定位估计算法[J]. 兵工学报, 2013, 34(5): 561-566. ZHU Ming-qiang, HOU Jian-jun, LIU Ying, et al. Target locating estimation algorithm based on adaptive scaled unscented kalman filter [J]. Acta Armamentarii, 2013, 34(5): 561-566. (in Chinese) [2] Zhang J, Wu C D, Zhang Y Z, et al. Energy-efficient adaptive dynamic sensor scheduling for target monitoring in wireless sensor networks[J]. ETRI Journal, 2011, 33(6): 857-863. [3] Yan X Y, Zhong Y, Song A, et al. A novel multihop range-free localization based on kernel learning approach for the internet of things[J]. Wireless Personal Communications, 2015, 87(1): 269-292. [4] Forrest S B, Pang Y L, Zhou W J, et al. Coverage-based lossy node localization for wireless sensor networks[J]. IEEE Sensor Journal, 2016, 16(11): 4648-4656. [5] 温龙飞, 崔灵果, 张百海, 等. 不均匀布置传感器网络定位优化算法[J].兵工学报, 2013, 34(5): 639-643. WEN Long-fei, CUI Ling-guo, ZHANG Bai-hai, et al. Research on location algorithm for nonuniformly deployed sensor networks[J]. Acta Armamentarii, 2013, 34(5): 639-643. (in Chinese) [6] Chen Z P, Li D Q, Huang Y R, et al.Event-triggered communication for time synchronization in WSNs[J]. Neurocomputing, 2016, 177: 416-426. [7] Mohamadi H, Salleh S, Razali M N, et al.A new learning automata-based approach for maximizing network lifetime in wireless sensor networks with adjustable sensing ranges[J]. Neurocomputing, 2015, 153: 11-19. [8] Liu X, Zhang S G, Bu K. A locality-based range-free localization algorithm for anisotropic wireless sensor networks[J]. Telecommunication Systems, 2016, 62(1): 3-13. [9] Zhang X P, Hu B J. An improved DV-Hop algorithm using hop-count information and geometric constraint[C]∥2011 7th International Conference on Wireless Communications, Networking and Mobile Computing. Guangzhou, China: IEEE, 2011. [10] Wu G, Wang S, Wang B, et al. A novel range-free localization based on regulated neighborhood distance for wireless ad hoc and sensor networks[J]. Computer Networks, 2012, 56(16): 3581-3593. [11] 夏少波, 邹建梅, 朱晓丽, 等. 基于跳数区域划分的DV-Hop改进算法[J].传感技术学报, 2014, 27(7): 964-969. XIA Shao-bo, ZOU Jian-mei, ZHU Xiao-li, et al. Improved DV-Hop algorithm based on regional division of hop count[J]. Chinese Journal of Sensor and Actuators, 2014, 27(7): 964-969. (in Chinese) [12] Chen G N, Chu Y L, Sun M T. Neighbor-based hop size estimation for dense sensor networks[J]. Journal of Information Science and Engineering, 2015, 31(3): 879-896. [13] Han S J, Lee S J, Lee S H, et al. Node distribution-based localization for large-scale wireless sensor networks[J]. Wireless Networks, 2010, 16(5): 1389-1406. [14] Sarita G, Hossain A K M M, Kanchana K. A hop-count based positioning algorithm for wireless ad-hoc networks[J]. Wireless Networks, 2014, 20(6): 1431-1444. [15] Shang Y, Ruml W. Improved MDS-based localization[C]∥Proceedings of the Conference on Computer Communication. Hong Kong, China: IEEE, 2004: 2640-2651. [16] Kuo J C, Liao W J.Hop count distribution of multihop paths in wireless networks with arbitrary node density: modeling and its applications[J]. IEEE Transactions on Vehicular Technology, 2007, 56(4): 2321-2331. [17] Bettstetter C, Eberspacher J.Hop distances in homogeneous ad hoc networks[C]∥57th IEEE Semiannual Vehicular Technology Conference. Jeju, Korea: IEEE, 2003: 2286-2290. [18] Heath M T. Scientific computing-an introductory survey [M].Boston: McGraw-Hill Press, 2005. Node Localization Algorithm Based on Hop-countQuantization in Wireless Sensor Networks ZHANG Shi, ZHANG Bai-hai, WANG Fei-fan, GUAN Zi-xiao ( School of Automation, Beijing Institute of Technology, Beijing 100081, China) A novel algorithm based on hop-count quantization and extended Kalman filter based on multidimensional scaling (MDS-HE) is proposed to improve the localization accuracy of nodes in wireless sensor networks. The integer hop-count can be transformed into a real number hop-count by partitioning a node’s one-hop neighbor set into three disjoint subsets and estimating the distance between nodes by the areas of the intersection regions of hop ring segmentation. The transformed real number hop-count is a more accurate representation of distance between nodes. The real number hop-count matrix is applied to the multidimensional scaling (MDS) method, and the extended Kalman filter is applied to refine accurately the coordinates of nodes. The localization performance of MDS-HE algorithm is simulated and analyzed in WSNs which is composed of nodes deploying randomly over a region. Simulated and experimental results show that the performance of the MDS-HE algorithm outperforms the DV-Hop method and the classical MDS method in the case of different number of nodes. The MDS-HE algorithm is exceedingly accurate in case of the enough anchor nodes. information processing technology; wireless sensor network; localization; multidimensional scaling; hop-count quantization; extended Kalman filter 2016-08-16 国家自然科学基金项目(61573061) 张石(1985—), 男, 博士研究生。 E-mail: zhangshi1985@126.com 张百海(1966—), 男, 教授, 博士生导师。 E-mail: smczhang@bit.edu.cn TP393.032 A 1000-1093(2017)05-0932-08 10.3969/j.issn.1000-1093.2017.05.013

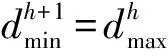

2 基于邻域划分的跳数量化





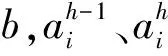

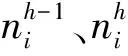
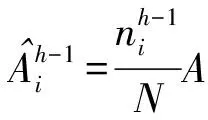





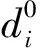




3 基于跳数量化的MDS定位算法


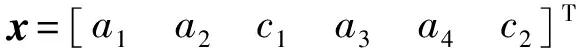


4 EKF算法



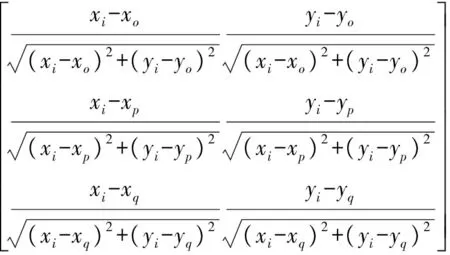



5 仿真分析






6 节点定位实验



7 结论

