考虑自动驾驶仪动态特性和攻击角约束的鲁棒末制导律
杨靖, 王旭刚, 王中原, 常思江
(南京理工大学 能源与动力工程学院, 江苏 南京 210094)
考虑自动驾驶仪动态特性和攻击角约束的鲁棒末制导律
杨靖, 王旭刚, 王中原, 常思江
(南京理工大学 能源与动力工程学院, 江苏 南京 210094)
针对制导弹箭打击机动目标时带攻击角约束的末制导问题,考虑自动驾驶仪动态特性以及目标机动不确定性对制导过程的影响,结合积分滑模与动态面控制方法,设计了一种新型鲁棒末制导律。自动驾驶仪的动态特性以含扰动的2阶动力学模型来表征,目标机动引起的模型不确定性以光滑非线性扰动观测器来估计。滑模面取视线角速率与视线角偏差的组合形式,且引入剩余飞行时间,以使制导弹箭在整个末制导过程中过载性能良好。依据李雅普诺夫稳定性理论证明了闭环系统中视线角速率与视线角偏差均最终一致有界任意小。通过数值仿真与弹道成型制导律及非奇异滑模制导律进行了对比,验证了该末制导律的有效性与优越性。
兵器科学与技术; 末制导律; 攻击角约束; 积分滑模; 动态面控制; 扰动观测器
0 引言
火炮武器系统在战场中反应迅速,能够提供强大且持续的火力支援,是未来部队联合作战的重要组成单元。随着现代战争理念的发展,远程压制、精确打击及高效毁伤等成为适配弹箭的发展方向。在一些实际应用中(如反坦克、反舰船及近程反导等),若制导弹箭能以一定的攻击角度命中目标,可以充分发挥其战斗部威力,提高杀伤效果,同时也降低了战争成本。因此,研究制导弹箭带攻击角约束的精确末制导问题具有重要的现实意义。
自从Kim等[1]针对再入式飞行器首次提出带攻击角约束的最优末制导律以来,很多学者针对不同研究对象,开展了带攻击角约束的末制导律研究。总的来说,分为两大类:1)假设目标机动已知,依据不同的性能指标,设计含攻击角约束的最优末制导律[2-5];2)将目标机动视为外部扰动,研究含攻击角约束的鲁棒末制导律[6-13]。
在应用最优控制理论的设计中,通常将含攻击角约束的末制导律问题转化为线性二次型最优控制问题,从而可得到解析形式的最优制导律。Zarchan[2]证明了在弹目速率不变、目标常值机动、制导系统无动力学滞后的条件下,使得脱靶量为0 m,且需用过载平方积分最小的制导律为弹道成型制导律(TSG)。此外,其引入零控脱靶量的概念,阐述了偏置比例制导律[3-4]与弹道成型制导律本质上是一致的。张友安等[5]针对固定目标,考虑弹体1阶动力学滞后,设计了一种带攻击角约束的最优末制导律。Cho等[6]针对以一定攻击角打击任意机动目标的情形,引入零控碰撞三角形,将平面内非线性弹目相对运动模型线性化,设计了一种新型含攻击角约束的最优末制导律。该方法仍需要目标的状态信息完全已知,但是在实际应用中,很多的目标状态无法准确测得,从而其应用受到限制。
在含攻击角约束的鲁棒末制导律设计中,通常将目标机动视为外部扰动,期望闭环系统对目标机动等因素引起的模型不确定性具有很好的稳定性与鲁棒性。作为鲁棒控制方法的一种,滑模控制具有对内部或外界的匹配扰动不敏感、控制精度高且算法简单、易于实现等特点,应用较为广泛。Rao等[7]将视线角速率偏差与视线角偏差的线性组合作为滑模面,设计了一种含攻击角约束的滑模末制导律。Kumar等[8]以视线角速率偏差与视线角偏差构建了一种非奇异滑模面,设计了一种含攻击角约束的有限时间收敛的非奇异滑模末制导律。上述方法都存在初始过载饱和的现象,这对内环自动驾驶仪提出了较高的要求。当自动驾驶仪回路带宽不够高的情况下,制导性能受到很大影响。因此,有必要在设计含攻击角约束的制导律中考虑内回路自动驾驶仪的动态特性。
当考虑内回路自动驾驶仪的动态特性,会使得整个系统的阶次较高,反步法适合处理该问题。反步法是一种递推设计方法,可以将高阶系统的控制律设计问题转化为对一系列低阶系统的交互设计。刁兆师等[9]将自动驾驶仪回路视为1阶动力学滞后,针对地面固定目标,应用反步法设计了一种带攻击角约束的末制导律。He等[10]引入线性阻尼,以视线角速率偏差与视线角偏差构建了一种非奇异滑模面,将自动驾驶仪回路视为2阶动力学环节,利用反步法设计了一种含攻击角约束的末制导律。但是,反步法中存在多次反步时“微分膨胀”的问题。
为了解决多次反步设计出现的“微分膨胀”问题,Swaroop等[11]结合非线性阻尼、积分反步及多面滑模控制的优点,提出了动态面控制方法。该方法不仅避免了反步设计中的“微分膨胀”问题,且不需要系统扰动项满足利普希茨连续条件。熊少锋等[12]以视线角速率偏差与视线角偏差构建了一种非奇异滑模面,将自动驾驶仪近似为1阶惯性环节,采用非奇异滑模与动态面控制方法,设计了一种含攻击角约束的末制导律。张尧等[13]引入非线性饱和函数及非线性阻尼,构建了一种新型积分型滑模面,将自动驾驶仪回路近似为2阶动力学环节,采用动态面控制方法,设计了一种含攻击角约束的新型末制导律。积分型滑模可使得系统从一开始就处于滑动模态,从而整个过程中不受扰动的影响。但是上述设计都未考虑自动驾驶仪模型的不确定性。
鸭式布局的制导弹箭为最小相位系统。因此,将其内回路自动驾驶仪的动态特性描述为含扰动的2阶动力学过程更为合理。
基于上述考虑,本文以含扰动的2阶动力学过程表征内回路自动驾驶仪的动态特性,结合积分滑模与动态面控制方法,设计了一种新型鲁棒末制导律,即积分滑模动态面控制末制导律(ISMDSG)。受弹道成型制导律的启发,在滑模变量的定义中引入剩余飞行时间,来改善整个末制导过程中的过载性能。采用扰动观测器补偿目标机动以及弹目速率变化引起的模型不确定性的影响。依据Lyapunov稳定性理论证明了视线角速率与视线角偏差均最终一致有界任意小,即实现了以一定的攻击角命中目标。
1 问题描述
1.1 平面内弹目相对运动模型
假设制导弹箭为轴对称外形,具有滚转稳定系统,采用侧滑转弯机动模式。因而,可实现三通道解耦,仅考虑纵向平面内的运动。纵向平面内的弹目相对运动关系如图1所示。

图1 平面内弹目相对运动关系Fig.1 Projectile-target relative movement in plane
图1中,Oxy为地面参考惯性坐标系;R为弹目相对距离;λ为弹目视线角;v、θ、a分别表示速度、弹道倾角和加速度;末端攻击角θimp定义为制导弹箭末端速度vPf与目标末端速度vTf之间的夹角。可得纵向平面内的弹目相对运动关系
(1)
对(1)式中的第2式求时间的导数,结合(1)式中的其他各式,可得视线角速率的动力学模型:
(2)
h=aP(1-cos(θP-λ))+aTcos(θT-λ)-

(3)
由此可知,h含目标机动及目标速度变化引起的扰动。
1.2 自动驾驶仪模型
实际中,外环制导回路生成的加速度指令是通过内环自动驾驶仪实现的。考虑到高频未建模动态的影响,自动驾驶仪的带宽不能过高。加速度指令与实际加速度之间总是存在一定的动力学滞后,这种时间延迟势必影响制导性能。因而,设计末制导律时,有必要考虑自动驾驶仪的动态特性。对于鸭式布局的制导弹箭,自动驾驶仪回路作为制导回路的一个环节,其动态特性可用含扰动项的2阶动力学近似表征:
(4)

1.3 机动目标模型
假设目标可由1阶动力学模型描述:
(5)

1.4 制导策略
Kumar等[7]的研究表明:不失一般性,假设目标末端速度倾角θTf=0,则当弹目位于碰撞三角形上时,末端视线角λf与攻击角θimp存在一一对应关系:

(6)
式中:vT/vP<1.
因此,前述制导律设计目标等价于:
(7)
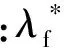
2 ISMDSG设计
2.1 制导律设计
为了使得末制导过程中的过载特性较为良好,类比弹道成型制导律,引入剩余飞行时间tgo,定义新变量s为
(8)



σ=s+z,z(0)=-s(0),
(9)
式中:辅助变量z满足
(10)
k为设计参数。

对(9)式求导,结合(2)式,整理得

(11)
(12)

最终目标为设计控制输入u,使得x1在有限时间内收敛到零点的任意小领域内。
动态面控制方法[12]结合了非线性阻尼、积分反步及多面滑模控制的优点,避免了反步设计中的“微分膨胀”问题,且不需要系统扰动项满足Lipchitz条件。因此,采用动态面控制方法对(12)式描述的问题进行设计,具体步骤为:
1) 设计虚拟控制量x2d. 定义第1个动态面:
S1=x1,
(13)
为使S1渐近收敛到零点附近,设计虚拟控制量为
(14)
式中:τ2>0为设计参数;
(15)

2) 设计虚拟控制量x3d.定义第2个动态面:
S2=x2-x2d,
(16)
为使S2渐近收敛到零点附近,设计虚拟控制量为
(17)
式中:τ3>0为设计参数;
(18)
K2>0为设计参数。
3) 设计实际控制量u. 定义第3个动态面:
S3=x3-x3d,
(19)
为使S3渐近收敛到零点附近,设计实际控制量为
(20)
式中:K3>0、ε3>0为设计参数;ρ3≥|da|.
2.2 稳定性分析
定义新的变量为
(21)
结合动态面Si,i=1,2,3的定义与(21)式,可得
(22)
对(13)式中的S1求导,并将(22)式第2式与(15)式代入其中,整理得

(23)
对(16)式中的S2求导,并将(22)式第3式与(18)式代入其中,整理得
(24)
对(19)式中的S3求导,并将(20)式与(17)式代入其中,整理得
(25)
对(21)式中的y2求导,结合(21)式与(14)式,整理得
(26)
对(21)式中的y3求导,结合(21)式与(17)式,整理得
(27)
由Young不等式,可得
(28)

(29)
考虑到现实情况,(1)式中的相关参数及其导数都有界,即存在M2、M3满足
(30)
由此可得
(31)
定义Lyapunov函数为
(32)
对(32)式求导,结合(29)式与(31)式,可得
(33)
选取参数K1、K2、K3、τ2、τ3满足:
(34)
式中:κ>0.
从而,有
(35)

(36)
依据比较原理,有
(37)
由此可见,S1、S2、S3、y2、y3是一致最终有界的。当κ足够大时,VL很快收敛到域Ω={VL≤ζ/κ}。这也意味着视线角速率与末端视线角偏差可以足够小。
综上所述,可得如下定理。

2.3 估计不确定项h
(12)式中含有不确定项h,可采用光滑非线性扰动观测器[15-16]获得。为保持本文的完整性,以下首先简述其要点,然后设计适用于本文问题的扰动观测器。
考虑单输入、单输出系统
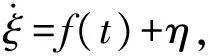
(38)

2阶形式的光滑非线性扰动观测器为
(39)
当ξ、η不存在测量噪声时,z1在有限时间内收敛于f(t);当ξ、η包含Lebesgue可测界为δ的噪声时,z1在有限时间内收敛于f(t)的领域内,其精度为|z1(t)-f(t)|≤μδ2/3,μ>0.
对照(2)式的第1式,记
(40)


3 仿真分析
为了验证本文所提出的ISMDSG的有效性与优越性,本节针对不同场景,做了大量仿真实验,并与弹道成型制导律(TSG)[2]及非奇异滑模末制导律(NTSMG)[8]进行了仿真对比分析。由于篇幅所限,仅列出部分仿真结果。
对于固定或匀速直线运动的目标,TSG方法给出的过载指令为
(41)

NTSMG方法给出的过载指令为
(42)

(43)
对于机动目标,NTSMG方法给出的过载指令为
(44)
式中:λT=θT-λ. 假设所有用到的目标信息已知。
以下仿真场景中,3种制导律中的参数保持不变,假设制导弹箭与目标均处于铅垂平面内。
3.1 情形1:目标固定
该仿真的目的是展示仅初始弹道倾角不同的情况下,要求垂直打击固定目标时,采用ISMDSG方法的末制导性能。
设地面固定目标的坐标为xT=5 000 m,yT=0 m;制导弹箭的初始位置为xP0=0 m,yP0=8 660.3 m. 这意味着初始弹目距离为R0=10 km,初始弹目视线角为λ0=-60°. 假设制导弹箭的速度大小为常数,取vP=500 m/s;制导弹箭的最大法向过载设为40g;2阶扰动近似自动驾驶仪模型中的参数为ξa=0.5,ωa=5 rad/s,其扰动项取为da=15sin (πt/3);期望实现对地面固定目标的垂直攻顶。取末制导初始时刻的弹道倾角θP0分别为15°、0°、-15°、-30°、-45°、-60°进行仿真。
图2~图5分别展示了不同末制导初始弹道倾角的情况下,采用ISMDSG方法的末制导时,制导弹箭的运动轨迹、弹目视线角速率、弹目视线角与期望的视线角偏差值和弹体的方向过载变化。图3表明弹目视线角速率在末端趋于0 °/s;图4说明实际弹目视线角收敛于期望的末端视线角。从而,采用本文所提出的ISMDSG方法可以在不同初始弹道倾角时实现对固定目标的垂直打击。从图5可以看出,末制导初始时刻不同的弹道倾角情况下,末制导初始阶段的法向过载差别较大,但最终的法向过载都趋于0g. 适当的末制导初始弹道倾角设计可降低末制导过程中的最大需要过载。

图2 情形1:ISMDSG方法不同初始弹道倾角时 弹箭的运动轨迹Fig.2 Case 1: projectile trajectories at different initial flight path angles via ISMDSG

图3 情形1:ISMDSG方法不同初始弹道倾角时 视线角速率的变化Fig.3 Case 1: line-of-sight rate profiles at different initial flight path angles via ISMDSG

图4 情形1:ISMDSG方法不同初始弹道倾角时 视线角偏差的变化Fig.4 Case 1: line-of-sight angle error profiles at different initial flight path angles via ISMDSG

图5 情形1:ISMDSG方法不同初始弹道倾角时 法向过载的变化Fig.5 Case 1: acceleration profiles at different initial flight path angles via ISMDSG
3.2 情形2:目标常值机动
本节针对常值机动目标,对比了本文提出的ISMDSG方法与TSG方法、NTSMG方法的末制导性能。


图6 情形2:弹目运动轨迹比较Fig.6 Case 2: comparison of trajectories of projectile and target

图7 情形2:视线角速率的变化比较Fig.7 Case 2: comparison of line-of-sight rate profiles
3.3 情形3:目标周期性机动
本节针对周期性机动目标,对比了本文提出的ISMDSG方法与TSG方法、NTSMG方法的末制导性能。


图8 情形2:视线角偏差的变化比较Fig.8 Case 2: comparison of line-of-sight angle error profiles

图9 情形2:法向过载的变化比较Fig.9 Case 2: comparison of acceleration profiles

图10 情形2:不确定项h及其估计值Fig.10 Case 2: uncertain term h and its estimated value 表1 情形2的脱靶量与飞行时间Tab.1 Miss distance and flight time for Case 2

参数TSG方法NTSMG方法M=500M=1000ISMDSG方法脱靶量/m542086093017飞行时间/s1654170218381731

图11 情形3:弹目运动轨迹比较Fig.11 Case 3 comparison of trajectories of projectile and target

图12 情形3:视线角速率的变化比较Fig.12 Case 3: comparison of line-of-sight rate profiles

图13 情形3:视线角偏差的变化比较Fig.13 Case 3: comparison of line-of-sight angle error profiles

图14 情形3:法向过载的变化比较Fig.14 Case 3: comparison of acceleration profiles

图15 情形3:不确定项h及其估计值Fig.15 Case 2: uncertain term h and its estimated value 表2 情形3的脱靶量与飞行时间Tab.2 Miss distance and flight time for Case 3

参数TSG方法NTSMG方法M=500M=1000ISMDSG方法脱靶量/m856127133031飞行时间/s2732295833382966
4 结论
针对制导弹箭打击机动目标时带攻击角约束的末制导问题,考虑自动驾驶仪动态特性对制导回路的影响,结合积分滑模与动态面控制方法,设计了一种新型鲁棒末制导律。依据Lyapunov稳定性理论证明了闭环系统中视线角速率与视线角偏差均最终一致有界任意小,即实现了以一定的攻击角命中目标。仿真结果表明:
1) 本文所提出的新型鲁棒末制导律,在存在目标机动不确定及自动驾驶仪含扰动的条件下,可使制导弹箭以给定的攻击角以高精度命中目标,且过载特性良好。
2) 当目标周期性机动时,若考虑攻击角约束,会使得制导弹箭部分弹道曲率较大,可能需要其在大攻角条件下飞行,导致气动非线性问题。另外,对于自主制导弹箭,较大的弹道曲率,可能导致导引头无法跟踪到目标。因此,在工程应用中要综合考虑。
References)
[1] Kim M, Grider K V.Terminal guidance for impact attitude angle constrained flight trajectories[J]. IEEE Transactions on Aerospace and Electronic Systems, 1973, 9(6):852-859.
[2] Zarchan P. Tactical and strategic missile guidance[M]. Reston, VA, US: American Institute of Aeronautics and Astronautics, Inc, 2012: 569-576.
[3] Byung S K, Jang G L, Hyung S H. Biased PNG law for impact with angular constraint[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(1): 277-288.
[4] 张春妍, 宋建梅, 侯博, 等. 带落角和时间约束的网络化导弹协同制导律[J]. 兵工学报, 2016, 37(3):431-438. ZHANG Chun-yan, SONG Jian-mei, HOU Bo, et al.Cooperative guidance law with impact angle and impact time constraints for networked missiles[J]. Acta Armamentarii, 2016, 37(3):431-438.(in Chinese)
[5] 张友安, 孙阳平, 方悦, 等. 带落角和末端攻角约束的最优末制导律[J]. 海军航空工程学院学报, 2013, 28(4):368-371. ZHANG You-an, SUN Yang-ping, FANG Yue, et al.Optimal guidance law with constraint on terminal impact angle and angle of attack[J]. Journal of Naval Aeronautical and Astronautical University, 2013, 28(4):368-371.(in Chinese)
[6] Cho H, Ryoo C K, Tsourdos A, et al.Optimal impact angle control guidance law based on linearization about collision triangle[J]. Journal of Guidance Control and Dynamics, 2014, 37(3):958-964.
[7] Rao S, Ghose D.Terminal impact angle constrained guidance laws using variable structure systems theory[J]. IEEE Transactions on Control Systems Technology, 2013, 21(6):2350-2359.
[8] Kumar S R, Rao S, Ghose D.Nonsingular terminal sliding mode guidance with impact angle constraints[J]. Journal of Guidance Control and Dynamics, 2014, 37(4):1114-1130.
[9] 刁兆师, 单家元. 考虑自动驾驶仪动态特性的含攻击角约束的反演递推制导律[J]. 宇航学报, 2014, 35(7):818-826. DIAO Zhao-shi, SHAN Jia-yuan. Back stepping guidance law with autopilot lag for attack angle constrained trajectories[J]. Journal of Astronautics, 2014, 35(7):818-826. (in Chinese)
[10] He S, Lin D, Wang J.Robust terminal angle constraint guidance law with autopilot lag for intercepting maneuvering targets[J]. Nonlinear Dynamics, 2015, 81(1/2):881-892.
[11] Swaroop D, Hedrick J K, Yip P P, et al.Dynamic surface control for a class of nonlinear systems[J]. IEEE Transactions on Automatic Control, 2000, 45(10):1893-1899.
[12] 熊少锋, 王卫红, 刘晓东, 等. 考虑导弹自动驾驶仪动态特性的带攻击角度约束制导律[J]. 控制与决策, 2015, 30(4):585-592. XIONG Shao-feng, WANG Wei-hong, LIU Xiao-dong, et al. Impact angle guidance law considering missile’s dynamics of autopilot[J]. Control and Decision, 2015, 30(4):585-592.(in Chinese)
[13] 张尧, 郭杰, 唐胜景, 等. 机动目标拦截含攻击角约束的新型滑模制导律[J]. 兵工学报, 2015, 36(8):1443-1457. ZHANG Yao, GUO Jie, TANG Sheng-jing, et al. A novel sliding mode guidance law with impact angle constraint for maneuvering target interception[J]. Acta Armamentarii, 2015, 36(8):1443-1457.(in Chinese)
[14] Yamasaki T, Balakrishnan S N , Takano H, et al. Sliding mode based intercept guidance with uncertainty and disturbance compensation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4):3331-3345.
[15] Shtessel Y, Edwards C, Fridman L, et al. Sliding mode control and observation[M]. NY, US: Birkhäuser , 2013: 30-34.
[16] Levant A. High-order sliding modes, differentiation and output-feedback control[J]. International Journal of Control, 2003, 76(9):924-941.
Robust Terminal Guidance Law with Autopilot Lag andImpact Angle Constraints
YANG Jing, WANG Xu-gang, WANG Zhong-yuan, CHANG Si-jiang
(School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, Jiangsu, China)
A novel robust impact-angle-constrained guidance law with autopilot lag is proposed based on integral sliding mode and dynamic surface control for guided projectiles. The inner-loop autopilot is characterized by an uncertain second-order dynamics. The sliding mode variable is defined as a combination of the line-of-sight (LOS) rate and the LOS angle error with time-to-go in order to realize the guidance strategy and achieve a good acceleration performance during interception. The smooth nonlinear disturbance observer is adopted to obtain the model discrepancies from target maneuver and the speed variation of target and interceptor. The stability of LOS rate and the LOS angular deviation is proved in the sense of the uniform boundedness and ultimate boundedness. Simulated results show the effectiveness and superiority of the proposed robust terminal guidance law compared to the trajectory shaping guidance law and the nonsingular terminal guidance law.
ordnance science and technology; terminal guidance; impact angle constraint; integral sliding mode; dynamic surface control; disturbance estimator
2016-10-24
国家自然科学基金项目(11402117)
杨靖( 1988—), 男, 博士研究生。 E-mail: jingyangnust@163.com
王旭刚( 1979—), 男, 副研究员。 E-mail: wxgnets@163.com
TJ765.2+2
A
1000-1093(2017)05-0900-10
10.3969/j.issn.1000-1093.2017.05.009

