双基地多输入多输出雷达收发四维角联合估计

陈显舟， 杨旭， 陈周， 白琳， 方海

(1.中国空间技术研究院西安分院， 陕西 西安 710100； 2.中国石油天然气管道工程有限公司， 河北 廊坊 065000)



双基地多输入多输出雷达收发四维角联合估计

陈显舟1， 杨旭1， 陈周2， 白琳1， 方海1

(1.中国空间技术研究院西安分院， 陕西 西安 710100； 2.中国石油天然气管道工程有限公司， 河北 廊坊 065000)

基于收发分置双L型阵多输入多输出雷达，提出了利用阵列接收数据的互相关去噪特性，进行目标辐射源收发四维角高精度联合估计的新方法。通过对匹配滤波后的阵列接收数据进行重构和互相关操作，可有效消除空间噪声影响，提高角度测量精度。将收或者发二维角的联合估计转化为两个一维估计，且只需对低维度矩阵进行特征分解，减轻了运算负担。利用特征值求取收或者发俯仰角，利用相应的特征向量构造出的虚拟阵列响应矩阵求取与其自动配对的收或者发方位角。仿真实验表明，该算法以较低的运算复杂度，实现了对空域多目标收发四维角的准确估计，估得的收或者发二维角能够自动配对，在低信噪比和短采样数据情形下，具有优良的角度估计性能。

兵器科学与技术； 多输入多输出雷达； 收发四维角； 互相关； 双L型阵

0 引言

双基地多输入多输出(MIMO)雷达[1]是一种新体制雷达，与传统相控阵雷达相比，在目标探测、杂波抑制、抗干扰、低截获、目标参数估计精度、目标识别等方面具有明显优势。MIMO雷达利用波形分集和空间分集技术，通过在发射端发射多个彼此相互正交的波形并在接收端经由匹配滤波处理将不同发射信号的回波彼此分离，可形成大量虚拟阵元，扩展了阵列的有效孔径，增加了阵列的自由度，能够增加可检测辐射源数量，有效提高参数估计的精度[2]。无需时间、角度、频率同步和收发站的数据传输，MIMO雷达通过估计目标的发二维角和收二维角实现对目标辐射源的定位。针对目标辐射源收发角的联合估计，是MIMIO雷达的研究热点，吸引了众多学者进行了大量细致的研究。文献[3-4]分别基于Capon算法和多信号分类(MUSIC)，采用二维谱峰搜索来估计目标收发角，运算负担极为繁重，不利于工程应用。文献[5]提出了一种基于旋转不变(ESPRIT)算法的目标发射接收角估计算法，降低了运算量，但需要进行角度配对。文献[6]改进了文献[5]的算法，估得的收发角能够自动配对。基于ESPRIT思想，文献[7]提出了一种存在阵列互耦条件下的收发角联合估计，解决了现有方法参数配对中存在参量兼并的问题。文献[8]提出了在空间目标数目未知导致信号子空间维数不能确定情形下的收发角联合估计。文献[9]提出了基于空域稀疏性的嵌套角度估计算法，改善了在同等数目虚拟阵元条件下的角度分辨力，增加了可探测目标数目。文献[10-12]算法实现了在空域色噪声或冲击噪声背景下的多普勒频率和收发角的联合估计，给出了在未知噪声背景和低信噪比条件下的角度估计方法。文献[13]提出了基于压缩感知的MIMO雷达角估计算法，改善了目前子空间分解算法的分辨力，提高了角度估计性能。为满足实际应用，从而降低运算复杂度，文献[14-16]通过将复数运算转化为纯实数运算，提出了基于酉子空间分解思想的角度估计算法，文献[17-21]提出了无需特征分解、短采样条件下的多维角快速估计方法。文献[22]基于联合对角化扩展阵列孔径和自由度思想，提出了基于双L阵目标收发四维角估计方法。文献[23]提出了基于快速正交匹配追踪算法的多普勒频移及收发角的联合估计算法。前述文献算法，要么是基于均匀线阵配置，无法实现目标收发四维角的估计，要么是能实现目标收发四维角的估计，却需要接收阵列样本协方差矩阵估计及特征分解过程，算法的运算复杂度较高，还需要额外的角度配对算法。本文基于双L型阵列模型，提出了双基地MIMO雷达收发四维角联合估计新算法，该算法充分利用接收阵列互相关矩阵消除噪声特性，从而提高角度估计性能。所提算法能够实现方位角和俯仰角自动配对，在低信噪比和短采样数据情形下，以较低的运算复杂度同时实现了目标收发四维角的高精度估计。

1 信号模型

图1 双基地MIMO雷达双L型阵列结构Fig.1 Double L-shaped arrays for bistatic MIMO radar

r(tl)=B(θr,φr)diag(α)AT(θt,φt)S(tl)+

W(tl),l=1,2,…,L,

(1)

利用2M-1个发射信号分别对每个接收阵元接收的Q个脉冲回波信号进行匹配滤波，将匹配滤波后的接收信号写成矩阵形式，可表示为

Z=HΣ+V，

2 算法描述

2.1 算法流程

根据阵列构型可知，提取A(θt,φt)的第1行到第M行构成Az(θt)，提取A(θt,φt)的第1行、第M+1行到第2M-1行构成Ax(φt)；提取B(θr,φr)的第1行到第N行构成Bz′(θr)，提取B(θr,φr)的第1行、第N+1行到第2N-1行构成Bx′(φr). 相应地，提取匹配滤波后的接收数据矩阵Z的第1行到第N行构成Zz′(θr)，提取Z的第1行、第N+1行到第2N-1行构成Zx′(φr)；提取Z的第(1-1)×(2N-1)+1，(2-1)×(2N-1)+1，…，(M-1)×(2N-1)+1行构成Zz(θt)，提取Z的第1行、第(M+1-1)×(2N-1)+1，(M+2-1)×(2N-1)+1，…，(2M-1-1)×(2N-1)+1行构成Zx(φt).

首先，求取Zz(θt)的自相关矩阵

(3)

其次，计算Zx(φt)、Zz(θt)的互相关矩阵：

(4)

式中：Vx(φt)、Vz(θt)分别为Zx(φt)、Zz(θt)对应的高斯白噪声矢量，信号和噪声矢量互不相关，不同轴上的接收噪声矢量互不相关，且满足

(5)

基于前面的模型假设，(4)式可以写为

(6)

由(3)式可得

(7)

式中：(·)†表示矩阵求伪逆操作；(·)-1表示矩阵求逆操作。

由(4)式、(6)式和(7)式可知

(8)

(9)

(10)

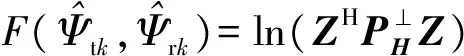
(11)

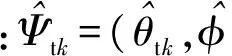
2.2 算法步骤及运算复杂度分析

所提算法的主要步骤如下：

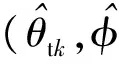
二维ESPRIT移不变类方法[12]，运算复杂度主要集中在协方差矩阵运算、协方差矩阵特征分解、移不变思想中对角阵的求解，算法的运算复杂度约为O(2(2N-1)2(2M-1)2Q+(2N-1)3(2M-1)3+8K2(2N-1)(2M-1)-4K2(2M-1)+4K3-4K2(2N-1)).

由此可以看出，经典的多重信号分类和移不变思想，在解决双基地MIMO雷达收发四维角联合估计方面，运算负担极为繁重。

文献[17]算法的运算复杂度主要集中在协方差矩阵运算、传播算子估计、特征值分解和求广义逆运算，其复杂度为O((2N-1)2(2M-1)2Q+(2N-1)2(2M-1)2+K2(2N-1)(2M-1)+3K2(M-1)(2N-1)+3K2).

所提算法运算复杂度相对于文献[17]方法略微增加，相对于经典二维 MUSIC谱峰搜索类方法、二维 ESPRIT移不变类方法，运算复杂度急剧下降，角估计性能介于二者之间。

3 仿真实验和分析

为了验证本文算法的有效性，设计如下仿真实验加以验证。双基地MIMO雷达双L型阵列结构如图1所示。假设发射和接收阵列阵元间距恒为半波长。假定M=N=5，在发射端，2M-1=9个阵元发射相互正交的Hardmard波形。

图2 目标四维收发角估计星座图Fig.2 2-D DOD and 2-D DOA scatter plots of 3 targets

从仿真结果可以看出，文献[17]方法估计目标四维收发角的误差较大，导致对目标的定位偏离真实位置。本文算法能够对空域四维收发角进行准确估计，并能对估得的收或者发二维角实现自动配对，可实现对多目标的有效测向定位。

实验2 假设空域目标数目K=1，收俯仰角θr=75°，收方位角φr=85°，发俯仰角θt=50°，发方位角φt=60°，接收端脉冲回波数目为Q=100，信噪比SNR在-10～10 dB之间变化时，做5 000次相互独立的蒙特卡洛实验，图3给出了文献[17]、本文算法收发四维角联合均方根误差(RMSE)和克拉美罗界(CRB)[21，26]随信噪比变化性能曲线，RMSE定义为

RMSE=

(12)

式中：Ne表示相互独立的蒙特卡洛实验。

图3 四维收发角联合RMSE随SNR变化Fig.3 RMSE of 2-D DOD and 2-D DOA versus SNR

从仿真结果可以看出，本文算法对匹配滤波后的阵列接收数据进行互相关操作，可有效消除空间噪声影响，在低信噪比条件下，收发四维角联合RMSE优于文献[17]算法。

实验3 假设空域目标数目K=1，收俯仰角θr=75°，收方位角φr=85°，发俯仰角θt=50°，发方位角φt=60°，信噪比SNR为0 dB，接收端脉冲回波数目Q在20～200之间变化，做5 000次相互独立的蒙特卡洛实验，图4给出了文献[17]算法、本文算法收发四维角联合RMSE和CRB随快拍数变化性能曲线。

图4 四维收发角联合RMSE随快拍数变化Fig.4 RMSE of 2-D DOD and 2-D DOA versus snapshots

从仿真结果可以看出，本文算法在短采样数据条件下，收发四维角联合RMSE优于文献[17]算法。

4 结论

本文针对发射与接收均为L型阵列的双基地MIMO雷达，提出了一种低复杂度的收发四维角联合估计算法。该算法通过对匹配滤波后的阵列接收数据进行重构和互相关操作，可有效消除空间噪声影响，改善空域多目标多维角度估计性能。

仿真实验证明了本文算法能够对空域多目标收发四维角进行准确估计，并能对估得的收或者发二维角实现自动配对，可实现对空域多目标的有效测向定位。在信噪比为-10 dB条件下，文献[17]算法的测角精度为2.5°，本文算法的测角精度优于2.0°，要达到2.0°测角精度，文献[17]算法的信噪比至少要达到-8 dB.

本文算法通过互相关去噪，在同等角度估计性能条件下，比文献[17]算法的信噪比要求“降低”了2 dB. 在信噪比均为0 dB条件下，要达到0.2°的测角精度，本文算法需要60个快拍累积，文献[17]算法至少需要90个快拍累积，本文算法比文献[17]算法的样本要求“减小”约30个快拍。因此，该算法改善了低信噪比和/或短采样数据情形下的空域多目标多维角度估计性能。

References)

[1] Li J, Stoica P. MIMO radar signal processing[M]. Hoboken, NJ, US: John Wiley & Sons, 2008.

[2] Bliss W, Forsythe W. Multiple-input multiple-output (MIMO) radar and imaging: degrees of freedom and resolution[C]∥37th Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, US: IEEE, 2003: 54-59.

[3] Li J, Conan J, Pierre S. Joint estimation of channel parameters for MIMO communication systems[C]∥2nd International Symposium on Wireless Communication Systems.Siena, Italy: IEEE, 2005: 22-26.

[4] Yan H D, Li J, Liao G S. Multitarget identification and localization using bistatic MIMO radar systems[J]．EURASIP Journal on Advances in Signal Processing, 2008, 8(2): 1-8.

[5] Chen D F, Chen B X, Qin G D. Angle estimation using ESPRIT in MIMO radar[J]. IEE Electronics Letters, 2008, 44(12): 770-771.

[6] Chen J L, Gu H, Su W M. Angle estimation using ESPRIT without pairing in MIMO radar[J]. IEE Electronics Letters, 2008, 44(24): 1422-1423.

[7] Zheng Z D, Zhang J Y, Kang K, et al. Joint DOD and DOA estimation for bistatic MIMO radar in the presence of mutual coupling[J]. Scientia Sinica Informationis, 2013, 43(6): 784-797.

[8] Xi Z F, Wu X F, Wu S Y, et al. Joint DOA and DOD estimation in bistatic MIMO radar without estimating the number of targets[J]. Journal of Electrical and Computer Engineering, 2014(3): 1-8.

[9] 杨杰, 廖桂生. 基于空域稀疏性的嵌套MIMO雷达DOA估计算法[J]. 电子与信息学报, 2014, 36(11): 2698-2704. YANG Jie, LIAO Gui-sheng. A spatial sparsity-based DOA estimation method in nested MIMO radar[J]. Journal of Electronics & Information Technology, 2014, 36(11): 2698-2704.(in Chinese)

[10] 郑志东, 袁红刚, 张剑云. 冲击噪声背景下基于稀疏表示的双基地MIMO雷达多目标定位[J]. 电子与信息学报, 2014, 36(12): 3001-3007. ZHENG Zhi-dong, YUAN Hong-gang, ZHANG Jian-yun. Multitarget localization based on sparse representation for bistatic MIMO radar in the presence of impulsive noise[J]. Journal of Electronics & Information Technology, 2014, 36(12): 3001-3007.(in Chinese)

[11] 洪升, 万显荣, 柯亨玉. 空间色噪声背景下双基地多输入多输出雷达低仰角估计方法[J]. 电子与信息学报, 2015, 37(1): 15-21. HONG Sheng, WAN Xian-rong, KE Heng-yu. Low-elevation estimation for bistatic MIMO radar in spatially colored noise[J]. Journal of Electronics & Information Technology, 2015, 37(1): 15-21.(in Chinese)

[12] Xu L Y, Zhang X F, Xu Z Z, et al. Joint Doppler frequency, 2D-DOD and 2D-DOA estimation for bistatic MIMO radar in spatial coloured noise[J]. International Journal of Electronics, 2015, 102(6): 1007-1021.

[13] Zhu W, Chen B X. Novel methods of DOA estimation based on compressed sensing[J]. Multidimensional Systems and Signal Processing, 2015, 26(1):113-123.

[14] Zheng G M, Chen B X. Unitary dual-resolution ESPRIT for joint DOD and DOA estimation in bistatic MIMO radar[J]. Multidimensional Systems and Signal Processing, 2015, 26(1): 159-178.

[15] Li J F, Zhang X F. Unitary subspace-based method for angle estimation in bistatic MIMO radar[J]. Circuits, Systems, and Signal Processing, 2014, 33(2): 501-513.

[16] 梁浩, 崔琛, 余剑. 基于ESPRIT算法的十字型阵列 MIMO雷达降维DOA估计[J]. 电子与信息学报, 2016, 38(1): 80-89. LIANG Hao, CUI Chen, YU Jian. Reduced-dimensional DOA estimation based on ESPRIT algorithm in monostatic MIMO radar with cross array[J]. Journal of Electronics & Information Technology, 2016, 38(1): 80-89.(in Chinese)

[17] 孙中伟, 张小飞, 吴海浪, 等. L型阵列双基地MIMO雷达的传播算子多维角度估计[J]. 应用科学学报, 2014, 32(1): 57-64. SUN Zhong-wei, ZHANG Xiao-fei, WU Hai-lang, et al. Multi-dimensional angle estimation in bistatic MIMO radar for L-shaped array with propagator method[J]. Journal of Applied Sciences-Electronics and Information Engineering, 2014, 32(1): 57-64.(in Chinese)

[18] Qin G D, Bao D, Liu G G, et al. Cross-correlation matrix root-MUSIC algorithm for bistatic multiple-input multiple-output radar[J]. Science China Information Sciences, 2015, 58(2):1-10.

[19] 张正言, 李小波, 徐旭宇, 等. 双基地MIMO雷达目标角度快速跟踪算法[J]. 信号处理, 2016, 32(6): 701-705. ZHANG Zheng-yan, LI Xiao-bo, XU Xu-yu, et al. Target angle rapid tracking algorithm for bistatic MIMO radar[J]. Journal of Signal Processing, 2016, 32(6): 701-705.(in Chinese)

[20] 李小波, 张正言, 王珽, 等. 双基地MIMO雷达相干目标的角度快速估计算法[J]. 信号处理, 2016, 32(3): 370-377. LI Xiao-bo, ZHANG Zheng-yan, WANG Ting, et al. Target rapid location of coherent target for bistatic MIMO radar[J]. Journal of Signal Processing, 2016, 32(3): 370-377.(in Chinese)

[21] 洪升, 万显荣, 易建新, 等. 基于单次快拍的双基地MIMO雷达多目标角度估计方法[J]. 电子与信息学报, 2013, 35(5): 1149-1155. HONG Sheng, WAN Xian-rong, YI Jian-xin, et al. An angle estimation method for multi-targets in bistatic MIMO radar with single snapshot[J]. Journal of Electronics & Information Technology, 2013, 35(5): 1149-1155.(in Chinese)

[22] Xia T Q. Joint diagonalization based 2D-DOD and 2D-DOA estimation for bistatic MIMO radar[J]. Signal Processing, 2015, 116: 7-12.

[23] Zhang D, Zhang Y S, Hu X W, et al. Fast OMP algorithm for 3D parameters super-resolution estimation in bistatic MIMO radar[J]. Electronics Letters, 2016, 52(13): 1164-1166.

[24] Friedlander B. The root-MUSIC algorithm for direction finding with interpolated arrays[J]. Signal Processing, 1993, 30(1): 15-29.

[25] Stoica P, Nehorai P. MUSIC, maximum likelihood, and Cramer-Rao bound[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1989, 37(5): 720-741.

[26] 郑志东, 袁红刚, 张剑云, 等. 运动双基地MIMO 雷达参数估计的克拉美罗界[J]. 电子与信息学报, 2014, 36(11): 2678-2683. ZHENG Zhi-dong, YUAN Hong-gang, ZHANG Jian-yun, et al. Cramer-Rao bounds for estimating parameter in the moving bistatic MIMO radar[J]. Journal of Electronics & Information Technology, 2014, 36(11): 2678-2683.(in Chinese)

4-D Angle Estimation for Bistatic MIMO Radar

CHEN Xian-zhou1， YANG Xu1, CHEN Zhou2， BAI Lin1， FANG Hai1

(1.China Academy of Space Technology (Xi’an), Xi’an 710100, Shaanxi, China;2.China Petroleum Pipeline Engineering Corporation, Langfang 065000, Heibei, China)

A new approach to high resolution estimation of four-dimensional (4-D) angle of multiple narrowband far-field signals is presented for bistatic multiple-input multiple-output (MIMO) radar with double L-shaped arrays. The spatial noise can be eliminated and the angle estimation performance is improved by constructing the matched array data and making full use of the cross-correlation matrix. The proposed method decouples the two-dimensional (2-D) direction-of-arrival (DOA) or 2-D direction-of-departure (DOD) estimation problem into two successive one-dimensional (1-D) estimation problems, and only requires eigenvalue decomposition of lower dimensional matrix, which can reduce the computational burden. The

or transmitted elevation angles are estimated using the eigenvalues, and the corresponding received or transmitted azimuth angles are estimated through the virtual array response matrix constructed by the corresponding eigenvectors. Numerically simulated results show that the proposed method can accurately estimate the 4-D angle of multiple spatial targets with lower computational complexity, and 2-D DOA or 2-D DOD could be paired automatically. The proposed method has better angle estimation performance in the situation of low signal-to-noise ratio and short data length.

ordnance science and technology; MIMO radar；4-D angle；cross-correlation matrix；double L-shaped array

2016-07-28

陈显舟(1985—)， 男， 工程师。 E-mail: xianzhouchen@126.com

TN958.2

A

1000-1093(2017)05-0917-07

10.3969/j.issn.1000-1093.2017.05.011