建立联系培养数感——读《如何培养学生的数感》一书有感

◇韩 东

《数学课程标准（2011）》指出：“数感主要是指关于数与数量、数量关系、运算结果估计等方面的感悟。建立数感有助于学生理解现实生活中数的意义，理解或表述具体情境中的数量关系。”初读这段话，我并不是特别明白其中的道理，总觉得有种说不出的感觉。当我读完《如何培养学生的数感》（[英]朱莉娅·安吉莱瑞著;徐文彬译）一书后，终于对数感有了感悟，它是一个人对数字和运算的一种灵活运用的倾向和能力。作者指出：“我们把孩子们具有的这种对数字之间关联的意识以及灵活地解决数字问题的能力称为其对数字的 ‘感觉’或‘数感’。孩子们具有‘数感’的典型特征是他们能对所遇到的数字模式和计算过程做出归纳，并能把新知识和已有知识相联系。”

一、在数字事实基础上建立联系

学生在实际活动中建立了很多数字事实，其中的一些数字事实对于培养学生的数感尤为重要。如果学生能把已知的数字事实与新运算联系起来，以此推断出新的知识，将会促进学生对数字系统逻辑本质的理解。比如，在得出3+5=8的结果后，他们自然就会把这个已知事实与“30+50、300+500”联系起来。再如，学生最早记住的数字事实是“两倍的数”（2+2，3+3等），可以让学生把其他数联想成“近似两倍的数”，“3+4”等同于 3+3+1 或 4+4-1。

不仅在加法上可以用数字事实建立联系，在其他运算中也常见。比如，学生知道了10-7=3，可能会立刻得出9-7的结果比前者少1，11-7的结果比前者多1。学生会在这些看似简单的计算中，体会到其中相互联系、相互影响的方面。再如，在乘法口诀的记忆方面，如果忘了六七是多少，则可以利用其他乘法口诀的数字事实，依据数之间的联系快速得到结果：（1）五七三十五，再加上七就是四十二；（2）六八四十八，再减去六就是四十二；（3）三七二十一，乘二就是四十二。正如安吉莱瑞所说：“在数字事实之间建立联系，不仅能使孩子们所要学习的乘法事实的数量减少，而且也会鼓励他们想出许多能够减少日后计算工作的策略。”

图1

由此可知，“建立这种数字关系不仅有助于孩子们从已知数字事实中推断出新的数字事实，而且也有助于他们建立新的计算策略。教师不应该阻止孩子们继续运用计数策略，而且要鼓励他们在已知数字事实和新问题之间建立相互联系”。

二、不必过早引入标准化竖式计算

标准化竖式计算具有简约化、自动化、普遍性、高效性等特点，历来是数学教学的重点，受到老师们的推崇。虽然它有如此多的优点，但也有一些不容忽视的缺点：“容易造成‘认知的被动性’和‘理解的中止’，因为这些方法与人们通常思考数字的方式不一样。”

所以，我们应适度推迟标准化竖式计算的出现，并把教学转变到让学生学会辨别数字模式和数字关系，并在两者之间生成联系的学习上，只有这样，才能使学生对数字产生“感觉”。多让学生使用个性化的笔记来解决问题，可能在初期阶段，学生的方法是杂乱无章、毫无效率的，这时教师要帮助每个学生把书面记录条理化，改善记录的组织形式并提高计算效率，使得学生不仅能理解解题方法，还能高效、灵活地解决问题。

例如：53×72。

算法一：（使用笔记）

100×72=7200，50×72=3600，3×72=216， 所以53×72=3600+216=3816。

算法二：（使用两倍法和两分法）

53×72=106×36=212×18=424×9=3816。

算法三：（使用拆数法）

53×72=53×8×9=424×9=3816。

算法四：（非标准化竖式计算）

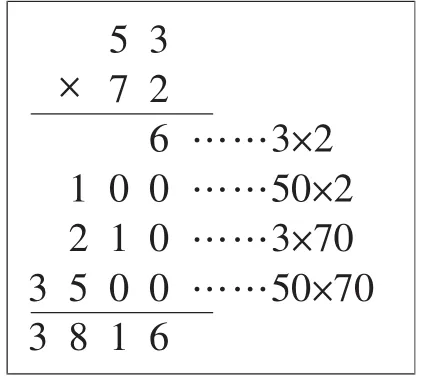
图2

从上面的不同算法中可以看出，学生灵活运用数字是至关重要的，有助于他们加深对数学规律的理解，而这些规律又是应用不同计算方法进行计算的基础。如果我们能延缓标准化竖式计算的出现，学生的注意力就有可能集中到解决问题的各种方法、数字关系的运算上，为以后解决其他数学问题打下基础。

三、重视学生心算的策略

斯图尔特·普朗科特（1979年）曾提出一个非常有影响力的观点：“计算器的出现为现代数学教育的发展提供了难得的机遇，我们不必再教给每一个公民复杂的计算方法。因此，我们可以放弃正规笔算，转而运用更适应于使用者心智和目的的方法……与反复使用并不为孩子们所理解的正规算法相比，用孩子们自己的心算方法进行计算更有利于加深他们对数字的理解。”

是的，心算是在学生对特定情境理解后，使用自己个性化的方法解决问题的策略，它具有短暂性、多变性、灵活性、积极性、整体性和有建设性等特点。只要这种心算被允许，你会发现学生更乐于用这种方法解题，而且这种方法的解题成功率远高于正规算法。其实不仅是学生，我们成人也是如此，科克罗夫特在1982年的报告中指出：“通过对工作场所中成年人运用数学的研究发现，在工作中，他们很少使用学校教授的笔算方法，而通常使用个性化的笔记来肯定自己的方法，这一方法有利于反映问题及其所涉及的数字结构。”所以我们应该重视学生心算的策略。

例如：64-37。

算法一：（顺序法）

（1）64-37=（64-30）-7=34-7=27。

（2）64-37=（64-4）-30-3=60-30-3=27。

算法二：（转换法）

64-37=（67-37）-3=30-3=27。

算法三：（拆十法）

64-37=（60+4）-（30+7）=（50+14）-（30+7）=（50-30）+（14-7）=27。

算法四：（同等加法）

64-37=（60+4）-（30+7）=（60+14）-（40+7）=（60-40）+（14-7）=27。

从以上的算法可以看出，学生在学习正式的笔算之前，就会形成自己独特的计算方法。使用这些独特的非正规的算法，将有助于学生利用已有数学事实，灵活解决问题。

再如：学习“多位数乘一位数”时有一道这样的连线题：

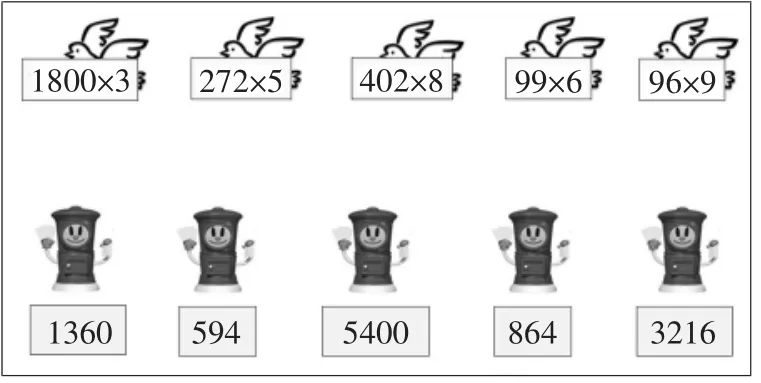
图3

解决这种连线题，根据特定规律和数学事实进行心算要比笔算简单得多。

1800×3和5400相连，因为因数末尾有两个0，下面的答案除了5400，都少于两个0；

272×5 和 1360 相连，因为 2×5=10，积的末尾应该是0，现在只有1360末尾有0了；

402×8 和 3216 相连，因为 2×8 末尾应该是 6。也可以不用末尾数判断，现在还剩下三道算式，402×8的积肯定是三个答案中最大的，所以只能是3216；

99×6和 594相连，96×9和 864相连， 因为99×6 大约是 600，96×9 大约是 900。也可以用本单元（人教版教材三年级上册第6页）刚学的99乘一个数“两边一拉，中间一插”的巧算法解决：99×6，用一个9与 6相乘得54，把54拉开，另一个9插到里面就行了。

学生根据具体情况，或是选用判断末尾数字，或是选用估算，或是选用“规律算”，这些心算法提升了学生根据具体情况判断和选择恰当的方法进行灵活计算的能力。