抓住关键词唤醒数学文本的生长力

◇刘 驰

数学具有结构化和层次化的特点，教师理所当然可以用结构化和层次化的方法来教数学。结构化和层次化的知识体系具有生长力，处于结构化和层次化节点的知识也应该具有天生的向四面八方延伸的鲜活的生长力。数学教学的本质不是教师教学生学，而是教师带领学生一起走向未知的数学世界，一起去发现数学文本生长之美，感受数学文本生长的力量。

课改以来，小学数学把原来的应用题拆分到各个相关知识点之后，相遇问题也因此安排在乘法运算律之后进行教学。为了让学生感受数学知识的生长力，在学习该部分内容后，笔者以关键词为线索设计了一节思维训练课，以下是教学片段。

师：（出示例7，如图1）这是大家上节课学习的内容。现在请大家很快地解决这个问题，然后和同桌说一说解决这个问题时有什么体会。

生：画线段图可以帮助我们找到不同的解题方法。

生:解题时运用了乘法分配律。

师：因为这是我们已经学过的知识，所以，即使能很快解答出来也不算高水平。这节课我们就从更高层次来研究这个问题，看看谁的水平高。

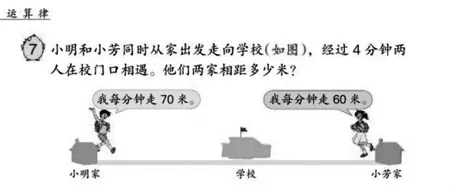
图1

师：请大家想一想，在这道题中有哪些比较重要的词？或者说，有哪些关键词？想好后在小组内交流一下。

生：同时出发。

师：这个关键词你是从哪儿找到的？

生：从文字里。小明和小芳同时从家出发走向学校。

生:相向而行。我是从图里看出来的。

师：我们不仅可以从文字表述中找出关键词，也可以分析示意图找出关键词。图可以帮助我们更直观地分析问题、解决问题。

生：同时到达。经过4分钟两人在校门口相遇。

生：两人行走的路线在一条直线上，是从图上看到的。

师：这位同学找到的关键词是：在一条直线上。我们对知识的研究已经透过表面越来越深入了，思考的水平也越来越高了。

生:我认为最后的问题“两家相距”也是一个关键词。

师：我们通过研究交流找到这么多关键词。如果去掉其中某一个关键词，例如，把“同时出发”去掉，我们刚才研究的问题会发生什么样的变化？请大家先独立想一想，也可以在纸上画一画帮助思考，然后在小组内交流一下。

生：如果去掉“同时出发”，小明和小芳既可以“同时出发”，也可以“先后出发”。“同时出发”这种情况我们已经研究过，“先后出发”这种情况我们设计的问题是：小明和小芳从家走向学校，小明先走1分钟，小芳才出发，小芳走了3分钟，两人在校门口相遇。两家相距多少米？（同时出示示意图）

师：请大家解决这个问题，并说一说你是怎样想的。

生：70×4＋60×3 或者 70＋（70＋60）×3， 在解决“先后出发”问题时，只需要在“同时出发”的基础上把先出发行的路程加上，实际上还是乘法分配律的应用。

师：如果去掉其他关键词呢？同样请大家先自己思考，然后再交流。

生：如果去掉关键词“相向而行”。小明和小芳除了“相向而行”，还可以“同向而行”和“相背而行”。“同向而行”这种情况，我们设计的问题是:小明和小芳同时从家走向学校，经过4分钟两人在校门口相遇，两家相距多少米？（同时出示示意图）70×4－60×4 或者（70－60）×4，就是用小明行的路程减去小芳行的路程，仍然是乘法分配律的应用。

生：“相背而行”这种情况，我们设计的问题是：小明和小芳同时从学校回家，经过4分钟两人同时到家。两家相距多少米？70×4＋60×4或者（70＋60）×4。

师：这和我们例题研究的“相向而行”这种情况有什么相同点和不同点呢？

生：行走的方向不同，一个是上学，一个是放学，解决问题的思路相同。

师:谁来汇报如果去掉“同时到达”这个关键词，又会发生什么变化？

……

数学教学不是教教材，而是教思维。教师在教学时可以挖掘教材背后的思维含量，唤醒数学文本的生长力，让学生体会数学由一个知识点向四处蔓延的生长之美。