观察、比较和想象：生长空间观念的土壤——以“认识平行四边形”一课为例

◇吴 贤

在“认识平行四边形”一课中，我以一组平面图形为观察素材，提出了不同的观察要求，在层层递进的比较中，在一次次富有挑战的想象中，尝试丰富儿童对几何图形的感受，突破儿童对高这一概念理解的难点，建立更为立体和丰厚的高的认识，沟通图形学习中各个概念之间的联系，让儿童的空间观念得到真正有生命力的生长。

一、在观察中唤醒已有认知

师：（出示图1）这些图形中，哪几个是你心目中的平行四边形？

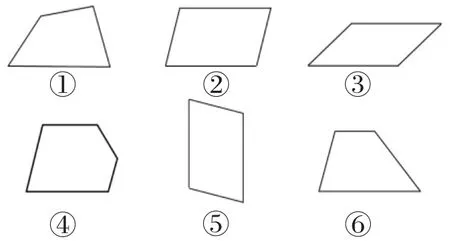
图1

生1：②号、③号和⑤号。

（其他学生纷纷表示赞同）

师：和他想法一样的同学请举手。的确，通过二年级的学习，我们凭感觉就能很容易从这些图形中正确挑选所有的平行四边形。不过，在对长方形、平行线等内容有了进一步认识之后，相信同学们再来观察平行四边形，一定会有更深入的发现。

思考：二年级时，学生已经初步认识了平行四边形，但那时候，他们对图形的区分基本还是凭借整体的感知和把握，或者说，凭借直觉和模糊的理解。如何将这种尚不能宣之于口的认识调取出来呢？在6个看似接近实则各有用意的多边形中遴选出平行四边形，很好地调动了学生已有的经验。①号虽然是四边形，但没有平行的对边；④号尽管有两组平行的对边，却不是四边形；⑥号图形只有一组对边平行。虽然学生还不能明确地概括出平行四边形的特点，但对于平行四边形的整体把握，却能够让其顺利地进行判断和选择，而这种数学观察、思考、判断的过程，正是学生将内部认识表征的过程，也是认识平行四边形的唤醒过程。

二、在操作中验证内部认识

师：为什么说②、③、⑤号图形是平行四边形呢？和其他图形比较，你觉得平行四边形具有什么特点呢？先在小组里说一说你的想法，再借助手边的工具，摆一摆、画一画，量一量、比一比，看看平行四边形究竟有怎样的特点。

（学生借助上面6个图形开展小组研究）

生1：我们把平行四边形上下两条边、左右两条边分别延长，发现它们永远不会相交，所以说平行四边形上下、左右的边分别平行。

生2：我们也有同样的发现，用证明平行的方法，推移尺子也能看出相对的边是互相平行的。

（学生操作演示）

生3：我们是在上下两条边之间画了很多条垂直线段，测量后可以看出，这些垂直线段的长度都是2厘米。我们知道，只有平行线之间的距离才能处处相等，所以这两条边一定互相平行。

师：大家发现，平行四边形有两组对边，它们分别平行。

生4：我们还测量了平行四边形的四条边的长度和四个角的度数。发现平行四边形对边不仅平行，长度也相等。另外，对角也相等。

生5：平行四边形虽然能被分成两个完全一样的三角形，但它不是轴对称图形，对折后不能完全重合。

师：通过刚才的研究，你们觉得平行四边形有哪些特点？

（学生从边、角等方面总结）

师：有了今天的认识，回头再看这几个不是平行四边形的图形，相信你们现在不仅仅是凭感觉，而是有了新的依据，对吗？

生：①号对边不平行，④号不是四边形，⑥号只有一组对边平行。

师：体会一下，我们在判断一个图形是不是平行四边形的时候，最喜欢用平行四边形的什么特点？

生：是不是平行，是不是四边形。

师：是的，再来读一读这个图形的名称，（和学生一起读）你有什么想说的？

生：平行四边形的名字就表示出它的特点了。

生：这个名字真是特别形象，一下子就告诉我们，对边平行、四边形，就是平行四边形。

思考：学生对平行四边形的特点有自己的理解，有的可能更关注边的位置关系，有的对边的长度、角的大小之间的相等关系有着自己的判断。让学生在小组中充分地交流、操作、验证，可以将他们对平行四边形模糊的猜测、认识变得更加具体、真实，相互的交流和补充又能让这些认识更为清晰和准确。

不过，对图形的认识，只有正例，还不足以凸显基本质特点。借助反例的辨析，从不同的角度再次体会，可以让学生对平行四边形的本质特点有更为清楚的体验。学生原有的空间感受，通过有价值的猜测、操作、验证活动得到了确认，在反例的再次审视中得到了提升，这让学生对平行四边形的内在特点，与其他图形的联系和区别有了更深刻的认识。

三、在比较中感知新的概念

师：继续观察②号和③号平行四边形，你还有什么发现？

生：这两个平行四边形四条边的长度分别相等，可是它们的形状却不一样。

师：的确，不仅如此，再观察一下，还有什么发生了变化？

生：这两个图形的大小不同。

生：图形中的角变了。

生：这两个图形的高也不相同。

师：真的吗？能用手势比画一下，你们所说的高到底在哪儿吗？

（学生有的用两手比画一组平行线，有的用手描画出一条垂直线段）

师：有了自己的理解后，能用合适的工具画出这条高，量出它的长度吗？每人选一个平行四边形，画一画，量一量。

（学生用三角尺画出上下对边之间的一条垂直线段）

师：和他画的方法差不多的同学请举手。

（大部分学生能画对，个别学生虽然画得不够标准，但都希望画出的是高）

师：这一条是高吗？（展示学生画出的不同位置的高）谁来说明一下？

生：是高，它和这一条高只是位置移动了一下，但依然是这里的一条垂直线段，长度也一样。

师：回忆我们画高的过程，什么样的线段是平行四边形的高？

生：只要是在平行四边形一组对边之间画出的垂直线段，就是这个平行四边形的高。

师：说得对，在平行四边形一组对边之间画出的垂直线段都是它的高，而这组对边就是这条高所对应的底。在画高的时候，我们可以从平行四边形一条边上的一点出发，向它的对边画一条垂直线段，这就是一条高。一般来说，高要用虚线来画，因为是垂直线段，还要加上直角符号。

思考：我们都知道，平行四边形的高是一个非常重要的新概念，在教材中，是借助起点和终点的方法定义这条图形内部的特殊线段的。在教学中，我们往往会把这个定义当作是数学上的一个规定，让学生按照文字的表述去理解和操作。但实际的学习效果往往不够理想。

值得我们思考的是，平行四边形的高的实质究竟是什么呢？生活中的高与数学上的高之间有没有联系？在教学中，我利用课始6个图形中两个特殊的平行四边形，让学生直观感知高的变化，模糊地找到高的位置。尝试画高后方法的比较，让学生真正体会到，平行四边形的高，实际上就是它一组对边间的垂直线段，且由于对边平行的特点，学生更容易理解高有无数条，处处相等。而建立在对边之间垂直线段这一理解上的高，也容易让学生对底的认识有所突破。

四、在想象中体会图形性质

让学生观察②号和③号这两个平行四边形，从而发现平行四边形边的长度不变，高却会发生变化。利用教具，让学生演示高的变化，体会在这一过程中，什么没有变、什么变了，说明平行四边形还很容易变形。

提问：当高最大的时候，平行四边形会变成什么图形？这个特殊平行四边形的高就是什么？

让学生体会平行四边形与长方形之间的联系和区别。

思考：这是一次对平行四边形的重新观察，从变与不变的角度，学生在静态的图和动态的框架的多次感知中，体会平行四边形易变形的特性。而观察中，对高的体会，还能巧妙地沟通平行四边形和长方形的联系，让学生在初步观察时产生的疑惑得到解答。

五、在矛盾中加深概念理解

师：（指②号和③号图形）这两个平行四边形，不仅高不相等，形状也发生了变化。想一想，还有没有这样一个平行四边形，它的四条边和这两个平行四边形分别相等，形状却不相同？

（生比画交流）

师：（出示平行四边形框架）这里有一个平行四边形，你能借助它说明你的想法吗？

生：这样的平行四边形还有很多，大家看，我只要推一点儿，这个图形的高就变了，但它的四条边的长度是不会变化的。

师：看来，平行四边形很容易变形。继续想象一下，这个图形的高如果不断变高，变到最高的时候，是怎样的呢？

生：高最高时，平行四边形就变成一个长方形了。这时候，高就跑到长方形的边上来了。

（学生边说边用框架演示）

生：我觉得长方形就是一个特殊的平行四边形。

师：通过这一次想象之旅，我们对平行四边形和它的高又有了新的认识。现在，请你在⑤号图形中，画出并量出它的底和高。

（学生画完后展示不同的画法）

师：观察②号和⑤号平行四边形，它们其实是完全一样的图形。（剪出一个图形与另一个重合）可是，同样的平行四边形，量出的底和高怎么会不相同呢？

生：一个是较长的边上的高，一个是较短的边上的高。

生：它们是画在不同的对边里的，对边不同，高的长度也不同。

生：我发现，底边比较短，高就比较长；底边要是比较长，高就比较短。

师：看来，观察的角度不同，底就不同，对应的高也不同，较长的边做底，对应的高就比较短；较短的边做底，对应的高就比较长。平行四边形的底和高是相互依存的，也是相互制约的。

思考：再次画高，既是一次对底和高的巩固练习，也为之后的比较提供了素材。在发现②号和⑤号其实是完全一样的平行四边形后，学生自然地产生这样的疑问：怎么同一个平行四边形，底和高却不同呢？在对这一问题的思考中，学生会基于各自的经验发现：同一个平行四边形，都能够画出两组不同的底和高，底和高必须对应存在，且长度之间是一种互相制约的关系。这为以后学习平行四边形的面积、灵活解决问题都提供了很好的经验基础。