用图形的面积表征分数的优势与局限性

◇游 迪 陈铭铭

在一次数学课上，安徽省阜阳市的陈铭铭老师在向学生解释如何用图形的面积表征分数时，遇到了困难。具体的题目如下：

如图1，阴影部分占图形的几分之几？请用分数表示。

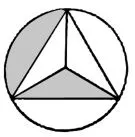
图1

陈老师发现，虽然绝大多数学生在回答上述问题时给出的答案是（标准答案），但也有部分学生的答案是。这样的结果引发了师生之间的讨论。那么，究竟是否可以算作一个正确的答案呢？为什么有的学生认为是正确的？

陈老师对学生的观点进行了简单归纳。有的学生在填写后这样解释：“很明显，圆被分为6份，阴影部分是其中的2份。”另一些学生认为：“由于在分数的教学过程中教师曾强调这个‘分’代表的是‘平均分’，因此的意义应该是把整体平均分成6份，取其中的2份。在这道题中，弓形和三角形的面积并不一定相等，可能不是‘平均分’，所以是不正确的。”还有的学生根据估计——弓形和三角形的面积看上去近似相等，得到阴影的面积是整体面积的。这种回答似乎也是合理的，况且，所以阴影部分也可以表示为。

为了探索这些不同的观点背后所代表的学生认知过程，以及其中的原因，本文将继续使用另一篇文章[1]中的分析框架，运用数学分析、认知分析和教学分析，讨论在教学过程中用图形的面积表征分数所具备的优势及潜在的局限性，从而探讨教学过程中存在的问题。正如文[1]中所说的那样，本文的最终目的是希望高校老师能够踏实地解决教学中的现实问题，而不是作脱离实际的空洞研究。同时，希望这样的分析框架和讨论形式，能帮助一线教师进入教学研究之门，从而成为探究型教师[2]。

一、数学分析

从数学角度分析，对分数意义的理解可以有多种方式。例如，Kieren教授提出了部分—整体、比、商、测量和算子五种理解方式[3]。其中，在有关“部分—整体”的理解中，“分数可以理解为表示部分与整体之间分割关系的数，即分数表示把一个整体平均分成b份，选出其中的a份”。

在本文开始的案例中，部分学生先从分数的“部分—整体”观出发，观察到图形中的圆被分成3个弓形和3个三角形。此时，图形中的部分和整体可以有多种可能。比如，学生可以将1个弓形加上1个三角形作为1个部分——扇形（如图2a），这样，整个圆被等分成了3个这样的扇形，阴影部分即是其中的1个。此时，答案为。学生也可以把图2a中的扇形分割成2个相等的部分（如图2b）。此时，整个圆被等分成6个部分，图2c是其中的1个部分，则阴影部分的面积就是。所以，不仅从数学的计算结果可以得出，从图形面积的角度考虑，当学生将图2c作为1个部分时，也可以是阴影部分正确的分数表征。当然，在陈老师所列举的学生解释中，并没有证据表明学生把扇形看成了如图2b所示的2个部分，学生这样思考的可能性不大。那么，为什么会有一部分学生认为答案是呢？我们来进行认知分析。

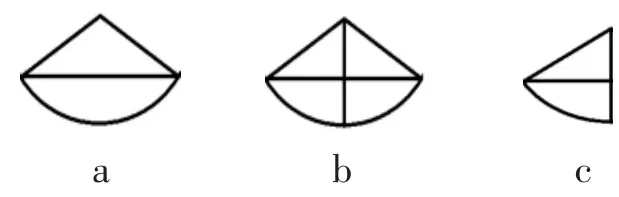
图2

二、认知分析

还有一部分学生是从分数数值的大小角度分析问题的，认为等于。比如，有的学生说：“我觉得和这两个分数是一样大的。”因此，阴影部分可以表示为。在这些学生的认知中，一方面，图形中阴影部分的面积确实是整体面积的；另一方面，圆被分成了6个部分，因此用来表示不够贴切，而在数量上与相等，又恰好符合图形被分割后份数的特征，所以用来表示阴影部分。

还有一部分学生从个数的角度来分析问题，将一个弓形或一个三角形均抽象为“1”个单位，将圆被分割之后的总体抽象为“6”个单位，进而认识到，阴影部分对应的是“2”个单位，最终得到这一答案。

尽管上面列举的例子不能完全概括学生可能存在的认知过程，但是根据以往的教学实践经验，上述三种情形都是可能存在的。这样的结果恰好可以说明用图形的面积表征分数在认知上的优势和局限性并存。用图形的面积表征的优势在于，它通常可以非常直观地把几分之几用部分和整体表征出来，一目了然。而用图形的面积表征分数的局限性主要有三个方面：（1）在用图形的面积表征分数时，总有一个潜在的假设，即每部分的面积完全相等。然而，在现实世界以及我们所使用的教学案例中，并不总是将若干个完全一样的图形作为一个整体（比如，一个整体中不可能所有部分都是正方形，也许会同时有正方形、三角形、圆形等）。那么，受限于画图工具所造成的误差，学生知识水平的限制（比如，没有学过某种图形的面积计算方法），以及题目所提供的信息的限制（比如，题目中没有给出计算面积所需要的条件）等，学生很难对各部分的面积是否相等作出精确判断，在解决问题时常常会涉及估算的过程，认为只要大体上面积相等即可。这就会让学生产生“是否真正需要平均分”这样的疑惑。（2）对于部分如何计数难以界定。例如，图3所示的长方形被分成了5部分，但每部分的面积不完全相同。阴影部分是其中的“1块”，其余还有“4块”。当用“块”作为单位时，这个“块”已经被抽象了，它没有面积大小的区分。尽管阴影部分的面积不是，但是它仍然是“5块”当中的“1块”，所以是。这样理解是有道理的。在图1所示的情境中，回答的一部分学生也正是参照了这样的思路——“6块”中的“2块”。在使用图形的面积表征分数时，面积单位往往是唯一的计数单位，从而会使学生忽视使用其他单位来计数的可能性和合理性。（3）用图形的面积表征分数时很难确定地表达整体和部分的相对性。例如，图4中的5个圆，可以从中看到什么样的分数？既可以以5个圆作为一个整体，此时学生看到的是（如图 4a）；也可以以2个圆作为一个整体，此时学生看到的是（如图4b）。得出怎样的结果取决于谁是整体，谁是部分。然而，如果仅从面积的角度来考虑，更多的学生则会认为2个圆的面积是整体面积的。

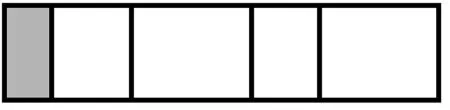
图3

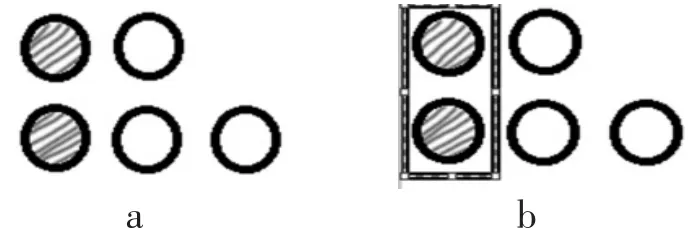
图4

那么，我们如何在教学过程中扬长避短呢？接下来的教学分析中，会就如何克服上述三方面的局限性分别进行简单讨论。

三、教学分析

通过数学分析和认知分析，大家可以了解到，无论学生给出的答案是还是，都有各自的道理，说明学生对分数的认知存在多样性，对同一个图形有不同的认知方式。这些认知方式有时是互补的，能够帮助学生进行正向迁移；而有时是相互交叉的，反而会让学生混淆分数的意义。教师要充分认识到用图形的面积表征分数时有着种种局限性，在教学过程中，应该通过各种不同的方式，让学生理解不同表征形式所代表的分数的含义。为此，在教学分析中，将通过一些案例，和大家一起讨论如何在一定程度上避免用图形的面积表征分数的局限性。

1.什么是平均分？

在认识分数教学的过程中，需要让学生认识到：一个图形不只有“面积”这一种属性；分数中的“平均分”，也不仅仅是“面积”的“平均分”；依据情境的不同，同一个图形可能代表着不同的含义。下面呈现这样一个案例：

某次体育课上，老师要求班上的16名学生站在如图5所示的操场上。操场被平均分成了8个区域。

图5

在学生列队的某一个瞬间，操场上的情况如图6所示，此时，已经有10名学生进入了操场，并且他们站在操场上的不同区域。请问：被圈出的部分占整体的几分之几？为什么你会认为这个分数代表它？

图6

当学生仅仅关注图5这个情境时，“平均分”代表的是整个操场被平均分成了8个区域。此时，无论是用图形的面积表征分数，还是抽象成数量后进行数量表征，都能得到：每个区域是整体的1。

8这突出了利用图形的面积表征分数问题的优势。

当学生看到图6时，情况就复杂多了。这个图形是将“平均分”的面积和“不平均分”的人数两种对象叠加而成的。在根据图6解决问题的过程中，不同的学生会有不同的思维过程。有的学生还是从图5中图形面积均分的角度进行思考，认为这2个区域占整个操场面积的。有的学生从人数均分的角度进行思考，认为因为班里一共有16名学生要进入操场，每名学生占班级学生的，所以3名学生占班级学生的；或者，他们会将进入操场的10名学生作为一个整体，那么3名学生占进入操场的学生的 3。还有的学生可能10同时从两个角度进行思考，他们认为方格并不是整个图形被“均分”后形成的图形，因此无法确定它所代表的分数；或者会将两种情形综合考虑，表达为

通过这个案例要向学生强调的是，我们在理解分数时总是要求等分，但这个等分可以是个数的等分、面积的等分、体积的等分、质量的等分……所以，在观察一个图形时，要了解使用分数所要表征或突出的是图形的哪一种特征，而不能将所有的特征混为一谈。

2.如何对分数进行计数？

学生在对分数的“均分”性质有一定了解后，所面临的另一个问题是针对图形的哪一个特征进行计数。事实上，虽然学生在概念上能够理解一个分数中每个部分所表示的含义，但是在实际解决问题的过程中，总是会因为一些主观的因素而忽略图形的一些潜在的特征。比如，下面一个例子：

请问：图7a和图7b中各有多少苹果？每幅图中的苹果占苹果总数的几分之几？

“图7a和图7b中各有多少苹果”这个问题考查的是学生对整数的计数，相信绝大部分学生会从“个数”的角度来计数，认为图7a中有7个苹果，图7b中有19个苹果。此时，学生很少会提出这些苹果在“颜色”“体积”“表面积”“质量”“成熟度”等方面的差异。这在整数的计数过程中无可厚非。然而，学生在回答问题“每幅图中的苹果占苹果总数的几分之几”时，这样的理解则有可能会产生较大的偏差。如果学生所给出的答案分别为，表明他们可能并没有意识到个数并不是这两幅图的唯一属性。换句话说，他们很自然地认为这个题目中对于分数中分子和分母的计数就是个数的计数，而非体积或其他特征的计数。虽然这样的答案是正确的，但是在教学过程中，我们需要让学生认识到这并不是唯一正确的答案，之所以可以得到这样的结果，是建立在以“个数”作为计数目标的前提下的。同样的一个例子，如果我们关注苹果的“质量”，那么所得到的结果就不一定是了，因为图7a中的7个苹果个头明显更大一些。

图7

3．谁是整体，谁是部分？

还有一个教学过程中亟待解决的问题是关于谁是整体、谁是部分的问题。一般而言，我们在教学中所给的例子所对应的整体和部分都是显而易见的。比如，在本文开头陈铭铭老师给出的用图形的面积表征分数的例子中，整体就是整个圆的面积，部分就是阴影部分的面积。事实上，我们知道现实生活中的整体与部分总是相对的、不断变化的。那么，如何帮助学生理解整体与部分的变化与相对性呢？图4是一个很好的例子。这里再举一个例子：

如图8所示，有30块巧克力。请你猜一猜，由这些巧克力组成的一大块巧克力可能是什么样子的？请画出所有你能够想到的巧克力的形状。

在你画出的各种形状的大块巧克力中，假如老师让你任选一种，并将这一大块巧克力分给你的同学，那么你可以分给多少名同学？每名同学可以分到几分之几？

图8

在这个案例中，学生首先需要思考的问题是30块巧克力可以组成怎样的一大块巧克力，也就是这些部分可以构成一个怎样的整体。通过学生的回答，可以发现有的学生会组成诸如5×6、3×10、2×15等不同形状的矩形巧克力，也可能是其他一些不规则形状的巧克力。此时，整体是在不断变化的。那么这些整体代表的是同一个整体吗？这是学生需要思考的问题。进一步，在第二个问题中，学生同样可以有不同的分配方式。有的学生会分给30名同学，每名同学分到1块，此时每名同学分到的是。也有的学生会选择只给2个最好的朋友吃，那么此时每人分到15块，占。不同的选择所对应的部分不同，其所代表的分数也不同。通过这样的案例，能够让学生了解到分数的整体和部分并不是绝对的，会根据你所关注的对象产生变化。

4．回到图形面积问题。

当学生对“什么是平均分？如何对分数进行计数？谁是整体、谁是部分”这些问题有了一定的了解之后，再回到最初陈铭铭老师的问题，他们就可以认识到：针对图形的不同特征（面积或个数等）进行计数，所得到的结果都是有道理的，并且他们不会因为这两种方式所得到的结果存在差异而产生混淆。

四、结语

本文通过数学分析、认知分析和教学分析的教学研究手段，对分数教学过程中用图形的面积表征分数的优势和局限性，以及相应的教学措施进行了分析与讨论。在用图形的面积表征分数时，存在着如何理解“等分”，如何对部分进行计数，以及如何体现整体与部分的相对性等局限性。教师可以通过学生对图形的各种不同形式的认知来设计教学过程，以达到帮助学生理解分数意义的目的。在对分数进行教学的过程中，应尽可能让学生理解：通过多种图形或不同的组合来对分数进行表征，可能对分数结果产生影响，仅仅采用图形的面积这一种方式，会让学生过于依赖对图形面积的判断，而忽视其他的特征，从而对学生理解分数产生影响。

分数的教学只是数学教学中的一部分。本文的最终目的是希望通过这样一种方式，为广大一线教育工作者提供一种视角，依靠数学分析、认知分析和教学分析这样一种框架，帮助教师了解到如何使用类似的框架进行其他教学案例的分析，鼓励更多教师参与到这种解决教学现实问题的研究中，从而能够让更多的教育研究者和教师共同致力于具体的改进数学教学的工作，提升自身的专业素养和研究能力，了解学生的思维过程，逐渐成长为一名具有教学研究能力、熟悉一线教学工作的探究型教师，同时也让高校的老师参与到这样的教学研究中来。

[1]游迪.数学教学中合情推理策略的使用：挑战与机遇[J].小学教学（数学版）,2017（7/8）.

[2]蔡金法,聂必凯，许世红.新世纪数学课程与教学研究丛书·做探究型教师[M].北京：北京师范大学出版社，2015.

[3]Kieren T E.The rational number construct:Its elements and mechanisms[M].Recent research on number learning,1980.