纯电动汽车横摆力矩滑模控制

刘 旭， 张袅娜， 周长哲， 李昊林

(长春工业大学 电气与电子工程学院， 吉林 长春 130012)



纯电动汽车横摆力矩滑模控制

刘 旭， 张袅娜*， 周长哲， 李昊林

(长春工业大学 电气与电子工程学院， 吉林 长春 130012)

建立了七自由度整车模型和非线性轮胎模型,通过线性二自由度车辆模型得到车辆质心侧偏角和横摆角速度的理想值。基于滑模变结构控制理论，以汽车质心侧偏角和横摆角速度为控制变量计算出车辆总的需求横摆力矩。采用二次规划法，根据总的需求力矩对车辆各个车轮进行转矩分配，实现车辆稳定性行驶。典型阶跃工况仿真验证了控制算法的有效性。

滑模控制； 横摆力矩； 稳定性； 仿真

0 引 言

汽车稳定性控制(Electronic Stability Program)主要为了实现汽车在不同行驶环境及运行工况下的良好驾驶性能，该种控制方法通过主动性的安全控制方法将车辆动力学指标作为反馈参数，调整车轮纵向力的状态实现对驾驶方向及稳定性能的控制[1]。随着科学的进步，控制理论技术在整车稳定性控制方面的应用得到快速发展，并成为当前国际上汽车安全领域的研究热点。

在车辆稳定性控制的研究中能够涉及到非常多的控制算法，这里面滑模变结构控制由于其极强的鲁棒性而受到人们关注。文中重点将车辆稳定性的两个重要参数即横摆角速度和质心侧偏角作为研究对象，基于滑模变结构控制理论设计汽车横摆稳定性控制系统，实现对整车稳定性横摆力矩控制。基于Matlab/Simulink搭建了七自由度整车动力学模型和轮胎模型。设计了滑模汽车横摆稳定性控制器。为了提高制动稳定性，采用二次规划法将总的需求横摆力矩在各个车轮进行转矩分配。最后选择正弦延迟行驶工况对控制算法进行仿真验证。仿真结果表明，所研究的控制算法能够有效提高汽车行驶稳定性。

1 整车模型

1.1 七自由度车辆模型

汽车在行驶时，通常车辆的运行情况和可调可控性都是由质心侧偏角与横摆角速度这两个重要参数反应出来的，这两个参数表征了车辆在不同程度上的稳定性能[2]。基于此，文中在车辆自由度的选择上就要找与这两个值紧密相关联的运动方向，即纵向运动、侧向运动和横摆运动。接着再对车辆模型进行简化设计成仅考虑与这两个值密切相关的3个方向加上4个车轮自身旋转方向的七自由度模型[3]，从而不考虑整车系统质心高度的改变、垂直、侧倾方向的运动等。整车简化模型如图1所示。

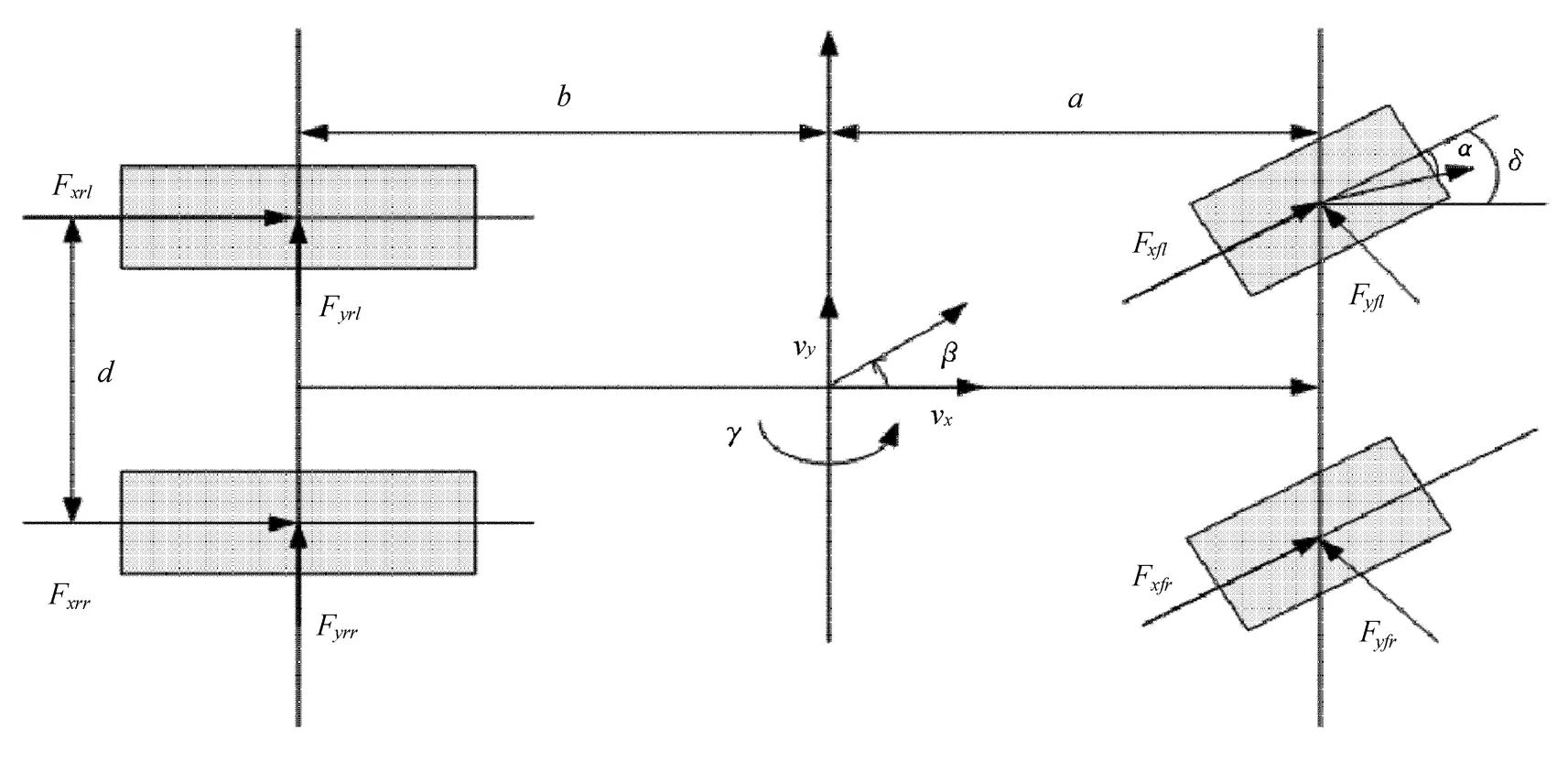
图1 整车简化模型

1)由图1所示，车辆纵向运动方程为：

式中：m----汽车质量；

vx----车辆纵向速度；

vy----侧向速度；

γ----横摆角速度；

Fxfr、Fxfl、Fyfr、Fyfl----分别为沿纵向和侧向的前右、前左轮胎力分量；

δ----前轮转角。

2)车辆侧向运动方程：

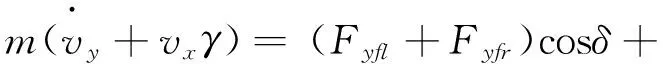
式中：Fxrr、Fxfr、Fyfr、Fyfl----分别为沿纵向和侧向的后右、后左轮胎力分量。

3)汽车横摆运动：

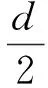
式中：I----车辆的转动惯量；

d----左右车轮轮距。

4)4个车轮的旋转运动：

式中：Jα----车轮转动惯量；

γij----车轮角速度；

Tdij----后轮驱动力矩；

Tbij----车轮制动力矩；

Fxij----车轮纵向力(i=f,r为前、后轮，j=l,r为左、右车轮，以上同)；

Rα----车轮滚动半径。

1.2 轮胎模型

目前使用较多的轮胎模型有：Fiala、UA、H.B.pacejka轮胎模型等。其中H.B.pacejka模型是目前为止使用最为广泛的模型之一。1987年由荷兰学者H.B.pacejka率先建立了H.B.pacejka轮胎模型[4]，它也叫做“魔术公式”轮胎模型，它是基于收集的实验数据经过处理分析得到的经验模型。

1)由此得到纵向力Fx、侧向力Fy和回正力矩的数学表达式[5]：

式中：DY----轮胎侧偏角曲线的巅因子；

BY----刚度因子；

EY----侧向力曲线曲率因子；

CY----侧向力曲线形状因子；

α----轮胎侧偏角；

Sh----水平偏移因子；

Svy----垂直偏移量。

2)其中各轮胎的垂向载荷[6]为

式中：Fzi----车轮垂直作用力(i=1,2,3,4)；

hc----质心高度；

lfs、lrs----簧载质量质心至前、后轴距离；

muf、mur----前、后轴非簧载质量；

huf、hur----前、后轴非簧载质量质心高度；

hf、hr----前、后轴侧倾中心离地面高度；

ax、ay----车辆纵、侧向加速度；

φ----汽车车身侧倾角。

2 基于滑模算法的整车横摆力矩控制

文中运用滑动模态变结构控制理论对总的需求横摆力矩进行计算，为了提高汽车操纵稳定性，基于二次规划法对需求横摆力矩进行各个车轮的转矩分配。

2.1 参考模型

由于线性二自由度模型能够较好描述驾驶员驾驶意图，车辆控制领域广泛采用线性二自由度车辆模型作各种控制方法用的参考模型。文中也选取车辆线性二自由度模型作为参考模型，基于线性二自由度参考模型得到理想横摆角速度和质心侧偏角值作为控制目标。

1)基于线性二自由度车辆模型的传递函数,求得质心侧偏角βd和横摆角速度γd的理想值表达式为[7]：

式中：K1----稳定性系数，取K1=2×10-3;

βmax----质心侧偏角最大值；

μ----路面附着系数；

g----重力加速度。

2)车辆的质心侧偏角是反映车辆稳定性的一个重要参数。质心侧偏角的定义如下[8]：

式中：vx----车辆纵向速度；

vy----车辆侧向速度。

2.2 基于滑模变结构汽车横摆稳定性控制

定义横摆角速度与质心侧偏角的实际值和理想值的偏差分别为：

由此设计滑动模态控制的切换函数为：

式中，k>0，且k值越大，其收敛速度越快。由此系统的动态特性为：

由于前轮转角较小可忽略不计，并且是通过后轮毂电机施加稳定性控制，可认为前左、前右轮的纵向力相同，由此将式(3)简化可得[7]：

由此可知，附加的横摆力矩为：

将式(18)代入到式(17)中,可得：

将式(19)代入到式(16)中,可表示为：

(20)

为了减少系统的扰动，定义切换控制率为：

式中:η----设计参数，且η>0。

由此可得总的需求横摆力矩为：

(22)

为了避免系统出现抖振现象，采用饱和函数代替符号函数：

式中：v----边界层厚度。

由此得到最终的需求横摆力矩为：

2.3 基于二次规划法的转矩分配控制策略

二次规划法是一种非线性规划的特殊类型，其目标函数是二次的，而约束是线性等式或不等式。首先根据纵向力及总的需求横摆力矩，采用控制分配理论即基于二次规划法进行优化分配，计算出每个车轮实际控制力矩。

汽车的行驶速度较高时，由于前轮的转向角度较小，所以不考虑车轮转角引起的纵向力改变，即总的纵向力与总的需求横摆力矩可以表示为[9]：

将上式改为矩阵的形式如下：

式中：

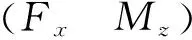
基于优化分配控制理念，在确保车辆有较好的稳定性前提下，提出以输出力加权平方和最小确定优化目标为[9]：

电机所提供的力矩大小受电动机外特性约束[10]：

式中：i----分别代表i=xfl,xfr,xrl,xrr对应前左、前右、后左、后右的轮胎方向。

对于纵向力同样也要受到路面附着条件以及垂向载荷的约束[10-11]：

式中：μ----路面附着系数;

Fzi----各车轮垂向载荷，如式(6)～(9)所示。

文中采用二次规划法对总的需求横摆力矩进行优化分配，根据上述优化目标以及约束条件，提出二次规划标准形式为[9]：

式中：Qm----对角阵代表控制幅值。

最后采用有效集法对总的需求横摆力矩优化问题进行求解，得到最佳横摆力矩分配方法。

3 veDYNA仿真结果分析

TesisDYNAware是一款专为车辆动力学控制装置及控制算法开发的快速虚拟仿真的车辆模型。 通过在Matlab/Simulink环境中搭建整车转矩控制策略，并与veDYNA动力学仿真软件进行实时连接，构建出纯电动汽车转矩控制方法仿真模型。该模型中主要实现对行驶路面、转矩控制方法、整车动力学系统、驾驶员模型及多种操作行为部分建模仿真。仿真选取的电动汽车参数为：a=1.12m,b=1.49m，d=1.39m,m=1 766kg,Iz=2 400kg·m2。为证明模型的合理性，选用具有代表性的阶跃转向工况来模拟车辆的实际运行情况。车辆的初始速度设定为90km/h，稳定行驶1s后，方向盘转角输入由0rad阶跃到1.2rad(约施加68°前轮转角)。

图2 方向盘转角阶跃输入

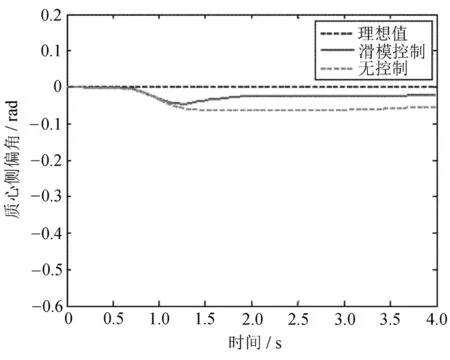
图3 质心侧偏角曲线

图4 横摆角速度曲线

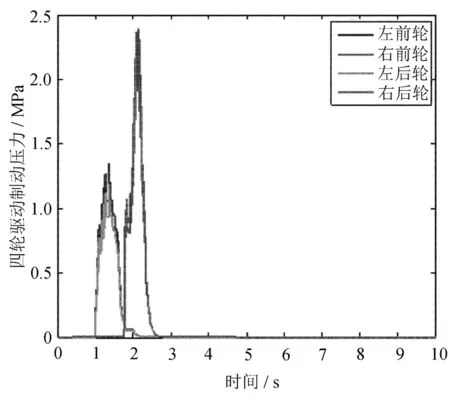
图5 车辆四轮制动压力

由图2～图5可知，施加滑模控制后车辆运动，其横摆角速度和质心侧偏角能够较好跟踪理想值，而无控制车辆横摆角速度和直线侧偏角相对理想值偏差大且最终出现了失稳状态。

4 结 语

基于滑模变结构控制理论设计汽车横摆稳定性控制系统，决策出车辆总的需求横摆力矩和基于二次规划法实现附加横排力矩分配方法，使车辆有效跟随理想横摆角速度和质心侧偏角，有效提高了车辆行驶的稳定性。

[1] 郑水波,韩正之,唐厚君.汽车稳定性控制[J].自动化博览,2005(4):22-24.

[2] 丁海涛.轮胎附着极限下汽车稳定性控制的仿真研究[D].长春:吉林大学汽车工程学院，2003.

[3] 余卓平,玛源,熊璐.分布式驱动电动汽车动力学控制发展现状综述[J].机械工程学报,2013,49(8):105-114.

[4]HiroshiFujimoto,NaokiTakahashi.Motioncontrolofelectricvehiclebasedoncorneringstiffnessestimationwithyaw-momentobserver[C]//IEEEInternationalAdvancedMotionControl,2006:206-211.

[5]FujimotoH,YamauehiY.Advaneedmotioncontrolofelectricvehiclebasedonlateralforceobserverwithactivesteering[C]//IEEEInternationalSymposiumonIndustrialElectronics.Bari,Itaily: [s.n.],2010:3627-3632.

[6] 玄圣夷,宋传学,靳立强，等.基于多级鲁棒PID控制的汽车稳定性控制策略[J].吉林大学学报:工学版，2010，40(1):13-18.

[7] 张金柱,张洪田,孙洪涛.电动汽车稳定性的横摆力矩控制[J].电机与控制学报,2012，12(6):75-79.

[8] 何铮斌.转向工况下四轮驱动汽车扭矩分配控制研究[D].重庆:重庆大学，2012.

[9] 余卓平,杨鹏飞,熊璐.控制分配理论在车辆动力学控制应用[J].机械工程学报，2014,50(18):100-107.

[10] 杨鹏飞,熊璐,张康,等.分布式电驱汽车稳定性控制策略设计与试验[J].机械工程学报，2013，49(24):128-143.

[11] 韦丽君,陈廷卫,张冰.水田农用车动力总成位置的分析[J].长春工业大学学报：自然科学版，2013，34(3):268-272.

Sliding control for electric vehicle yaw moment

LIU Xu, ZHANG Niaona*, ZHOU Changzhe， LI Haolin

(School of Electrical & Electronic Engineering, Changchun University of Technology, Changchun 130012， China)

Both a 7 degree of freedom (DOF) vehicle model and a nonlinear tire model are established, and the optimal values of both the sideslip angle of gravity center and yaw rate are obtained with a linear 2 DOF vehicle model. By means of sliding structure-varied theory, the required yawing moment is calculated with sideslip angle and yaw rate as control variables. The quadratic programming is applied to distribute the torquefor each wheel based on the overall moment needed to ensure that vehicle moves smoothly. Simulation with stepinput show that the method is effective.

sliding control; yaw moment; stability; simulation.

2016-04-21

国家高技术研究发展计划(863计划)基金资助项目(2012AA110904)； 国家重点基础研究发展计划(973计划)基金资助项目(2011CB711205)； 吉林省科技厅科研基金资助项目(20126008)

刘 旭(1990-)，女，汉族，吉林桦甸人，长春工业大学硕士研究生，主要从事控制科学与工程专业方向研究,E-mail:35719625@qq.com. *通讯作者：张袅娜(1972-)，女，汉族，吉林长春人，长春工业大学教授，博士，主要从事非线性系统控制、故障诊断等方向研究,E-mail:zhangniaona@163.com.

10.15923/j.cnki.cn22-1382/t.2017.2.05

U 463.6

A

1674-1374(2017)02-0127-06