区间删失数据的3种统计模型分析及其SAS实现
张倩倩, 王纯杰, 佟知真, 李纯净
(长春工业大学 基础科学学院, 吉林 长春 130012)
区间删失数据的3种统计模型分析及其SAS实现
张倩倩, 王纯杰*, 佟知真, 李纯净
(长春工业大学 基础科学学院, 吉林 长春 130012)
借助SAS9.4中PROC ICLIFETEST、PROC ICPHREG过程步编写宏程序,同步实现了区间删失数据的生存函数估计、广义Log-Rank检验和PH类型回归模型的统计推断。结合回溯研究中368个样本HIV-1感染时间的区间删失数据给出实证分析。
区间删失; ICLIFETEST; 广义对数秩检验; ICPHREG; 宏程序
0 引 言
生存分析是对试验或调查得到的人或生物的生存时间数据进行推断,在医学实践中有着广泛应用。一般称给定事件的出现时间为生存时间[1],分析生存时间数据通常意味着解决3个问题:估计生存函数,比较处理组或者生存函数,评估协变量的影响或者依靠生存时间的解释变量。区间删失数据是生存时间中越来越常见的一种数据,在过去几十年里,出现了许多分析区间删失数据的统计方法。Turnbull[2]找到了类似右删失数据下的Kaplan-Meier估计的自相合算法来获得生存函数估计;王弄升[3]2012年利用SAS软件中宏程序%EMICM给出区间删失数据生存函数的估计;Sun[4]等把Log-Rank检验推广到区间删失数据中,提出广义对数秩检验;Finkelstein D M[5]给出区间删失数据的COX回归模型。但是基于SAS软件还没有完整的程序可以同步实现区间删失数据3种统计分析任务。因此,文中借助SAS9.4中PROC ICLIFETEST[6]、PROC ICPHREG过程步编写宏程序,实现了区间删失数据的生存函数估计、广义Log-Rank检验和PH比例风险类型的回归模型统计推断。
1 模型及方法介绍
1.1 区间删失的数据类型
设T为非负的随机变量,代表研究中个体的生存时间,对于区间删失数据,只能知道T落在某个区间内,即T∈(L,R],在这里L≤R。区间删失数据可分为Ⅰ型区间删失与Ⅱ型区间删失。Ⅰ型区间删失数据可以表示{C,δ=I(T≤C)},C代表观测时间,I(·)是示性函数。Ⅱ型区间删失数据是包括有限区间的区间删失数据(L,R),假设每个个体观测两次,L,R是两个随机变量,L≤R以概率1成立。
1.2 区间删失数据的非参数估计
1.2.1 EMICM算法[1]
SAS软件计算非参数生存函数的方法是EMICM法。该算法是一个把自相合与ICM算法简单结合的混合算法。考虑一个包含n个独立个体带有生存函数为S(t)的失效时间的研究。令Ti代表个体i(i=1,2,…,n)的生存时间。假设在Ti上的区间删失数据被观测如下:
O={(Li,Ri];i=1,2,…,n}

则区间删失数据的似然函数为:

NPMLE算法就是要最大化此似然函数。在自相合算法中对数似然为:

Wellner,Zhan[7]指出,当NPMLE存在且唯一并且对数似然函数连续可微的时候,EMICM算法收敛到NPMLE。应用EMICM算法需要选择一个收敛准则。这里选择基于Robertson[8]1988年提出的Fenchel优化条件。这种准则下如果满足
1.2.2 广义对数秩检验[1]

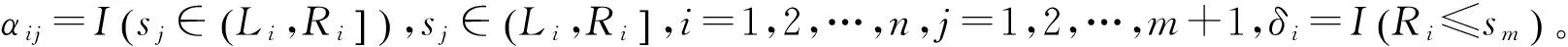
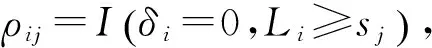
j=1,2,…,m
类似的对于第l组,l=1,2,…,p+1,且j=1,2,…,m时,在sj处失效数和在风险数的估计为:
为了检验H0,给出统计量
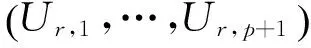
此检验统计量是服从自由度为P的卡方分布。
1.2.3 PH比例风险模型[1]


则似然函数的对数形式为:
利用极大似然函数的得分方程估计β,基准生存函数S0可由连续的阶梯函数来估计。
2 实证分析
2.1 区间删失数据及变量情况
数据来源于美国和欧洲的16个研究中心的第5中心[9],此中心采用回溯研究的方法,主要研究带有血友病的病人感染HIV-1的风险。血友病人的治疗血液制品来自于成千上万个捐赠者的血浆制成的Ⅷ型凝血因子和Ⅳ型因子,所以这些病人都存在感染HIV-1的风险。文中对病人的HIV-1感染时间只得到了区间删失数据,且病人依据他们每年获得血液制品的平均剂量被分配到不同的组。来自第5中心的368个病人的观测数据,不考虑进入研究的病人HIV-1抗体状态,不接受或接受低剂量(1~20 000U)的Ⅷ型凝血因子(两组病人的组别记为NF和LDF)见表1。
两组病人的数量分别为236和13,这些数据以季度为单位,0代表研究开始时间(1978年1月1日)。

表1 HIV-1感染数据
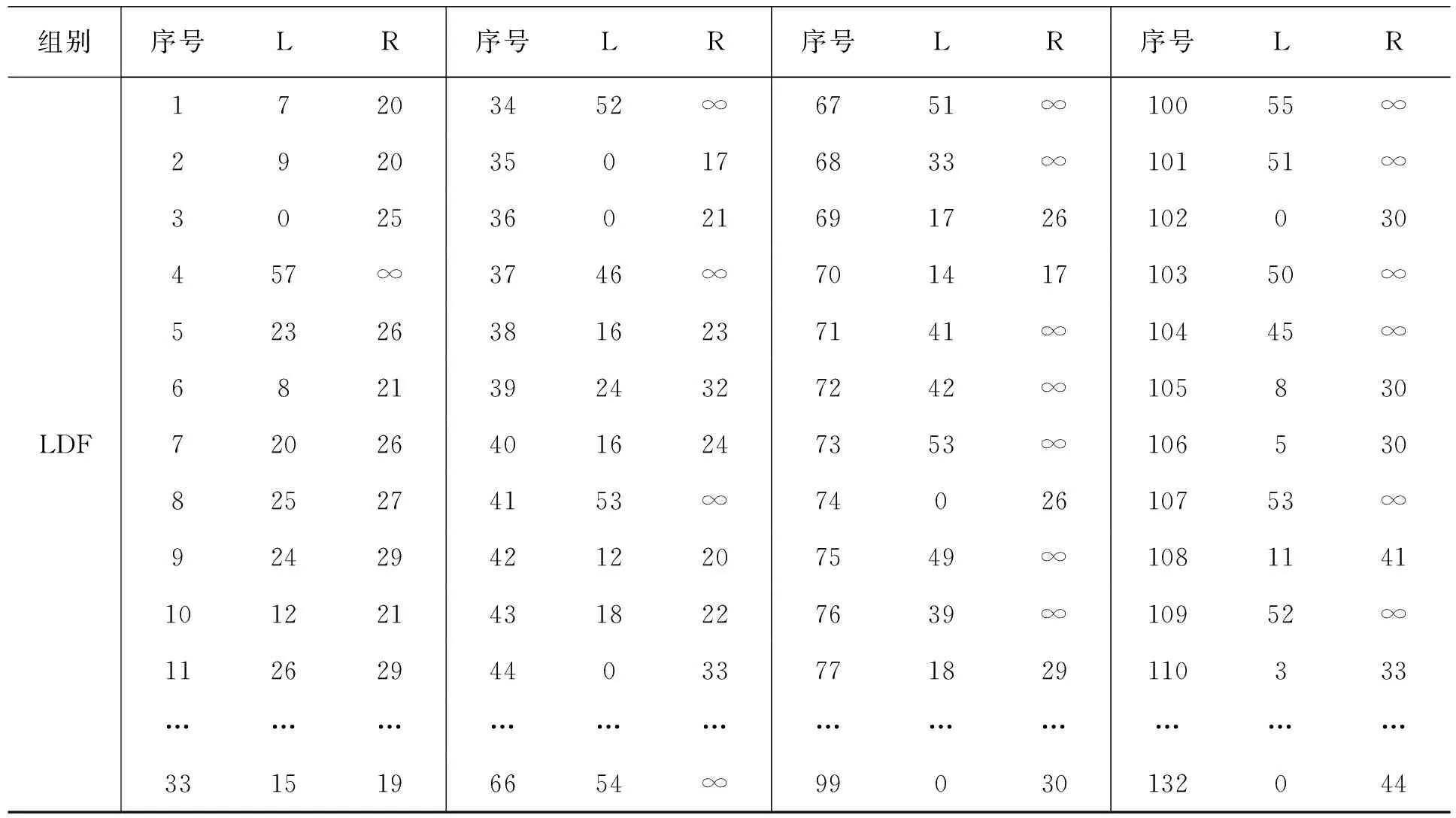
续表1
2.2 SAS程序
对于上述血友病患者HIV-1感染的区间删失数据,首先要分别建立两组的SAS数据集,然后用ICLIFETEST过程步估计出两个受试组HIV-1感染的时间生存函数,并检验两组生存曲线的区别,最后用ICPHREG过程步建立PH比例风险回归模型。区间删失数据3种生存统计分析可由SAS宏程序%ICLIFETEST-PHREG同步实现。
2.2.1 创建NF组的数据集
data NF;
input lTime rTime @@;
Stage=0;
datalines;
55. 55. 56. 54. 53. 57.
56. 56. 54. 56. 54. 55.
...;
run;
2.2.2 创建LDF组的数据集
data LDF;
input lTime rTime @@;
Stage=1;
datalines;
720 920 025 57.
2326 821 2026 2527
...;
run;
2.2.3 估计两组病人的生存概率及绘制生存曲线
data zq;
set LDF NF;
run;
proc iclifetest data=zq plot=s(cl) impute(seed=1234);/*ICLIFETEST过程步对应数据,画出带95%置信带的生存曲线图*/
strata stage;/*识别定义分组的变量*/
time (lTime,rTime);/*区间删失的左右观测时间*/
run;
2.2.4 两组病人数据的广义Log-Rank检验
proc iclifetest data=zq impute(seed=1234);
time (lTime,rTime);
test stage;/*检验的组别*/
run;
2.2.5 生存时间与协变量的PH比例风险回归
proc icphreg data=zq;
class Stage / desc;
model (lTime,rTime) = Stage / basehaz=pch(intervals=(10));/*协变量Stage与区间删失数据建立PH比例风险模型*/
hazardratio Stage;/*求风险比例*/
run;
上述5个程序是分别建立数据集,做区间删失数据的3种统计模型分析的SAS程序,对于临床试验得到的这类区间删失数据,如果利用SAS程序做分析,需要进行上述复杂的5个程序的运行,文中给出一个宏程序,同步实现上述模型分析。
2.2.6 区间删失数据同步实现3种统计任务的SAS宏程序%ICLIFETEST-PHREG
%macro iclifetest-phreg(data,var1,var2);
proc iclifetest data=&data plot=s(cl) impute(seed=1234);
strata &var1;
time (lTime,rTime);
run;
proc iclifetest data=&data impute(seed=1234);
time(lTime,rTime);
test &var1;
run;
proc icphreg data=&data;
class &var2/ desc;
model (lTime,rTime) = &var2/ basehaz=pch(intervals=(10));
hazardratio &var1;
run;
%mend;
%iclifetest-phreg(zq,stage,stage)
宏程序%ICLIFETEST-PHREG可以对含二分变量和其他协变量的区间删失数据同步实现生存函数的估计、广义的Log-Rank检验及PH比例风险类型的回归分析。其语法结构是:data:含二分变量和其他协变量的区间删失数据集;Var1:某一个二分协变量;Var2:做回归分析的所有的协变量集合。
2.3 结果分析
两个不同组的非参数生存估计与生存函数曲线的宏程序结果分别如图1和表2所示。

图1 NF组与LDF组估计的生存函数
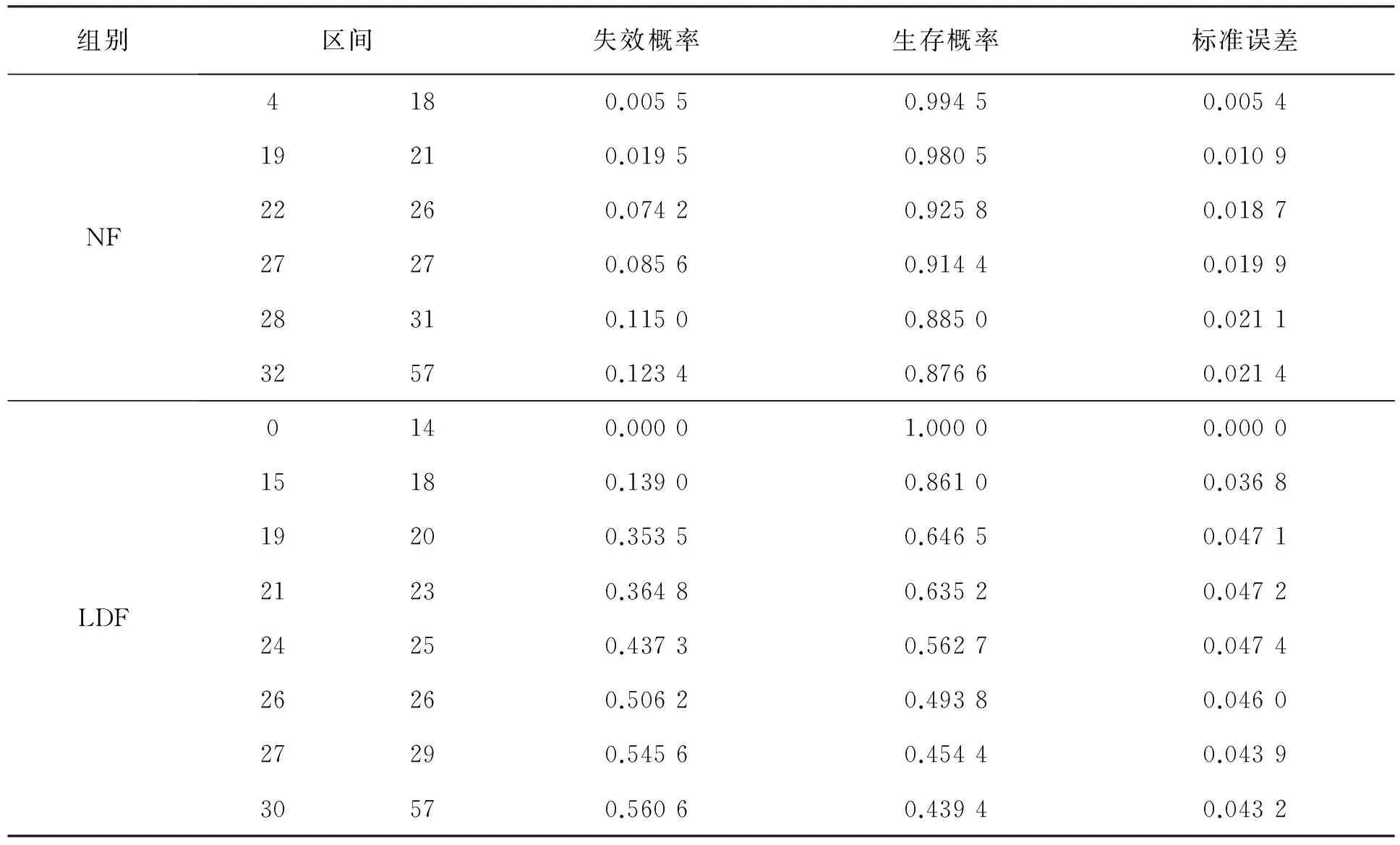
组别区间失效概率生存概率标准误差NF4180.00550.99450.005419210.01950.98050.010922260.07420.92580.018727270.08560.91440.019928310.11500.88500.021132570.12340.87660.0214LDF0140.00001.00000.000015180.13900.86100.036819200.35350.64650.047121230.36480.63520.047224250.43730.56270.047426260.50620.49380.046027290.54560.45440.043930570.56060.43940.0432
图1中相应的NF组的生存概率要大于LDF组的生存概率,即不接受Ⅷ型凝血因子的血友病实验组的生存概率要高于接受低剂量Ⅷ型凝血因子的实验组。表2中NF组的失效概率要小于LDF组的失效概率。
两组生存概率是否相等的检验结果及回归的显著性检验结果分别见表3和表4。

表3 检验两组生存概率是否相等

表4 回归的显著性检验
在显著性水平为0.05的情况下,表3和表4的p值均小于0.000 1,即拒绝原假设,LDF组和NF组的生存概率有明显区别。表4说明该回归模型参数是显著的。分组的风险比估计见表5。

表5 分组的风险比估计
表5结果显示,患有血友病的病人接受低剂量的Ⅷ型凝血因子组感染HIV-1病毒的风险概率要高于不接受组病人感染HIV-1病毒的风险,且是后者的7.360倍。
3 结 语
基于区间删失数据生存函数的估计算法除了EMICM算法还有自相合、ICM、Turnbull算法等。广义对数秩检验也成为检验生存函数是否相等的有用工具。实例说明,NF与LDF治疗组的生存函数有显著差异。回归模型检验出分组协变量对生存时间存在有效的影响。文中给出的SAS宏程序可以针对带有协变量的区间删失数据同步实现生存函数的估计、比较处理组及协变量对生存时间的影响这3种统计推断,对临床工作人员整理、分析实验结果有很大帮助。
[1] Sun J. The statistical analysis of interval-censored failure time data[M]. [S.l.]: Springer Science & Business Media,Inc,2006.
[2] Turnbull B W. The empirical distribution function with arbitrarily grouped, censored and truncated data[J]. Journal of the Royal Statistical Society,1976,38(3):290-295.
[3] 王弄升,张晋听,骆福添.含有区间删失数据时的生存函数估计及其SAS实现[J].中国医院统计,2012,19(1):1-4.
[4] Zhao Q, Sun J. Generalized log-rank test for mixed interval-censored failure time data [J]. Statistics in Medicine,2004,23(10):1621-1629.
[5] Finkelstein D M. A proportional hazards model for interval-censored failure time data [J]. Biometrics,1987,42(4):845-54.
[6] Guo C, Ying S, Gordon J. Analyzing interval-censored data with the ICLIFETEST procedure [J]. SAS Global Forum,2014,279:327-345.
[7] Jon A Wellner, Yihui Zhan. A hybrid algorithm for computation of the nonparametric maximum likelihood estimator from censored data [J]. Journal of the American Statistical Association,1997,439(92):945-959.
[8] Robertson T, Wright F T, Dykstra R L. Order restricted statistical inference [J]. Journal of the American Statistical Association,1990,85(410):111-112.
[9] Kroner B L, Rosenberg P S, Aledort L M, et al. HIV-1 infection incidence among persons with hemophilia in the United States and western Europe,1978-1990. Multicenter Hemophilia Cohort Study[J]. Journal of Acquired Immune Deficiency Syndromes,1994,7(3):279-86.
SAS-based study on three statistical models for interval censored data analysis
ZHANG Qianqian, WANG Chunjie*, TONG Zhizhen, LI Chunjing
(School of Basic Sciences, Changchun University of Technology, Changchun 130012, China)
Applying the procedures such as PROC ICLIFETEST and PROC ICPHREG in SAS9.4, we realize the statistic deduction for the survival function, Generalized log-rank test and PH regression for the interval censored data by means of macro programming. Interval censored data during the infection time from 368 samples are analyzed in the prospectively study.
interval censored; ICLIFETEST; generalized Log-rank test; ICPHREG; macro program.
2017-01-22
国家自然科学基金(青年基金)资助项目(11301037); 国家自然科学基金资助项目(11571051,11671054); 吉林省教育厅“十三五”规划项目(2016317)
张倩倩(1991-),女,汉族,山东德州人,长春工业大学硕士研究生,主要从事生存分析方向研究,E-mail:zhangqqxiao@163.com.*通讯作者:王纯杰(1978-),女,汉族,辽宁灯塔人,长春工业大学副教授,博士,主要从事生存分析方向研究,E-mail:cjwang2014@126.com.
10.15923/j.cnki.cn22-1382/t.2017.2.02
O 212.3
A
1674-1374(2017)02-0111-06

